* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
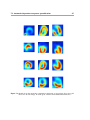
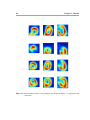
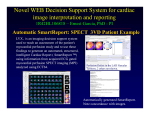
Download Segmentation and Alignment of 3-D Transaxial Myocardial Perfusion Images and
Aphelion (software) wikipedia , lookup
3D television wikipedia , lookup
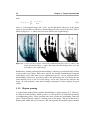
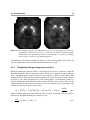
Medical imaging wikipedia , lookup
Indexed color wikipedia , lookup
Edge detection wikipedia , lookup
Computer vision wikipedia , lookup
Anaglyph 3D wikipedia , lookup
Spatial anti-aliasing wikipedia , lookup
Image editing wikipedia , lookup
Stereoscopy wikipedia , lookup
Stereo display wikipedia , lookup
Segmentation and Alignment of 3-D Transaxial Myocardial Perfusion Images and Automatic Dopamine Transporter Quantification Leo Bergnéhr April, 2008 Reg nr: LiTH-IMT/MI30-A-EX--08/465--SE Segmentation and Alignment of 3-D Transaxial Myocardial Perfusion Images and Automatic Dopamine Transporter Quantification Master’s Thesis in Biomedical Engineering at Linköping University by Leo Bergnéhr April, 2008 Reg nr: LiTH-IMT/MI30-A-EX--08/465--SE Supervisor: Joakim Rydell Examiner: Magnus Borga Abstract Nuclear medical imaging such as SPECT (Single Photon Emission Tomography) is an imaging modality which is readily used in many applications for measuring physiological properties of the human body. One very common type of examination using SPECT is when measuring myocardial perfusion (blood flow in the heart tissue), which is often used to examine e.g. a possible myocardial infarction (heart attack). In order for doctors to give a qualitative diagnose based on these images, the images must first be segmented and rotated by a medical technologist. This is performed due to the fact that the heart of different patients, or for patients at different times of examination, is not situated and rotated equally, which is an essential assumption for the doctor when examining the images. Consequently, as different technologists with different amount of experience and expertise will rotate images differently, variability between operators arises and can often become a problem in the process of diagnosing. Another type of nuclear medical examination is when quantifying dopamine transporters in the basal ganglia in the brain. This is commonly done for patients showing symptoms of Parkinson’s disease or similar diseases. In order to specify the severity of the disease, a scheme for calculating different fractions between parts of the dopamine transporter area is often used. This is tedious work for the person performing the quantification, and despite the acquired three dimensional images, quantification is too often performed on one or more slices of the image volume. In resemblance with myocardial perfusion examinations, variability between different operators can also here present a possible source of errors. In this thesis, a novel method for automatically segmenting the left ventricle of the heart in SPECT-images is presented. The segmentation is based on an intensity-invariant local-phase based approach, thus removing the difficulty of the commonly varying intensity in myocardial perfusion images. Additionally, the method is used to estimate the angle of the left ventricle of the heart. Furthermore, the method is slightly adjusted, and a new approach on automatically quantifying dopamine transporters in the basal ganglia using the DaTSCANTM radiotracer is proposed. Sammanfattning Nukleärmedicinska bilder som exempelvis SPECT (Single Photon Emission Tomography) är en bildgenererande teknik som ofta används i många applikationer vid mätning av fysiologiska egenskaper i den mänskliga kroppen. En vanlig sorts undersökning som använder sig av SPECT är myokardiell perfusion (blodflöde i hjärtvävnaden), som ofta används för att undersöka t.ex. en möjlig hjärtinfarkt. För att göra det möjligt för läkare att ställa en kvalitativ diagnos baserad på dessa bilder, måste bilderna först segmenteras och roteras av en biomedicinsk analytiker. Detta utförs på grund av att hjärtat hos olika patienter, eller hos patienter vid olika examinationstillfällen, inte är lokaliserat och roterat på samma sätt, vilket är ett väsentligt antagande av läkaren vid granskning av bilderna. Eftersom olika biomedicinska analytiker med olika mängd erfarenhet och expertis roterar bilderna olika uppkommer variation av de slutgiltiga bilder, vilket ofta kan vara ett problem vid diagnostisering. En annan sorts nukleärmedicinsk undersökning är vid kvantifiering av dopaminreceptorer i de basala ganglierna i hjärnan. Detta utförs ofta på patienter som visar symptom av Parkinsons sjukdom, eller liknande sjukdomar. För att kunna bestämma graden av sjukdomen används ofta ett utförande för att räkna ut olika kvoter mellan områden runt dopaminreceptorerna. Detta är ett tröttsamt arbete för personen som utför kvantifieringen och trots att de insamlade bilderna är tredimensionella, utförs kvantifieringen allt för ofta endast på en eller flera skivor av bildvolymen. I likhet med myokardiell perfusionsundersökningar är variation mellan kvantifiering utförd av olika personer en möjlig felkälla. I den här rapporten presenteras en ny metod för att automatiskt segmentera hjärtats vänstra kammare i SPECT-bilder. Segmenteringen är baserad på en intensitetsinvariant lokal-fasbaserad lösning, vilket eliminerar svårigheterna med den i myokardiella perfusionsbilder ofta varierande intensiteten. Dessutom används metoden för att uppskatta vinkeln hos hjärtats vänstra kammare. Efter att metoden sedan smått justerats används den som ett förslag på ett nytt sätt att automatiskt kvantifiera dopaminreceptorer i de basala ganglierna, vid användning av den radioaktiva lösningen DaTSCANTM . Acknowledgements This project has been carried out at Exini Diagnostics AB and I would like to thank everyone there for their support and friendliness. Special gratitude goes to my company supervisor, professor Lars Edenbrandt, who initiated the project and invited me to work on it. Thank you; bringer of good confidence! Additionally, I would like to thank my university supervisor, Joakim Rydell, at the Department of Biomedical Engineering. In the beginning of this project I had a lot of questions, to which you always had enlightening answers, despite completing a PhD at the same time. Finally, I give a special acknowledgement to my family and near friends; not for helping me while formulating mathematical expressions, but for just being there when I was not. Thank you! Table of Contents 1 Introduction 1.1 Background 1.2 Objectives . 1.3 Method . . 1.4 Outline . . 1.5 Notation . . 2 Scintigraphy 2.1 Nuclear medicine physics . . . . . . . . . . . . 2.1.1 Decay of radioactive isotopes . . . . . 2.1.2 Detection of radiation . . . . . . . . . 2.2 Single Photon Emission Computed Tomography 2.2.1 Image quality . . . . . . . . . . . . . . 2.3 Scintigraphic examinations . . . . . . . . . . . 2.3.1 Myocardial perfusion SPECT . . . . . 2.3.2 DaTSCAN Quantification . . . . . . . 2.4 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Image Segmentation 3.1 Segmentation methods 3.1.1 Thresholding . 3.1.2 Region growing 3.1.3 Active shapes . 3.2 Image registration . . . 3.3 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 The Morphon Method 4.1 Displacement field estimation . . 4.1.1 Quadrature phase . . . . 4.1.2 Least square solution . . 4.2 Displacement field accumulation 4.3 Displacement field regularisation 4.4 The model . . . . . . . . . . . . 4.4.1 Deformation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 2 2 3 4 . . . . . . . . . . . . . . . . . . 5 5 5 6 8 8 9 9 10 11 . . . . . . . . . . . . 13 13 13 14 15 15 17 . . . . . . . 19 20 20 24 24 25 26 26 . . . . . . . . . . . . 8 Table of Contents 4.5 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Rotation of Myocardial Perfusion Images 5.1 Pre-processing of images . . . . . . . 5.2 2-D Morphon segmentation . . . . . . 5.2.1 Locating the heart . . . . . . 5.2.2 Segmentation . . . . . . . . . 5.3 3-D Morphon segmentation . . . . . . 5.4 Angling of the heart . . . . . . . . . . 5.4.1 Angle estimation . . . . . . . 5.4.2 Rotation . . . . . . . . . . . . 5.5 Summary . . . . . . . . . . . . . . . 6 Dopamine Transporter Quantification 6.1 3-D Morphon segmentation . . . . . . . . . . . 6.1.1 Locating the basal ganglia . . . . . . . 6.1.2 Segmentation . . . . . . . . . . . . . . 6.2 Quantification . . . . . . . . . . . . . . . . . . 6.2.1 Weighted principal component analysis 6.3 Summary . . . . . . . . . . . . . . . . . . . . 7 Results 7.1 Segmentation and alignment of 3-D transaxial myocardial perfusion images . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.1.1 Segmentation . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.1.2 Alignment . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.2 Automatic dopamine transporter quantification . . . . . . . . . . . . . 7.2.1 Segmentation . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.2.2 Quantification . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 . . . . . . . . . 29 29 30 31 31 32 33 34 35 35 . . . . . . 37 37 38 39 40 41 43 45 45 45 46 46 52 52 Discussion 8.1 Segmentation and alignment of 3-D transaxial myocardial perfusion images . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8.2 Automatic dopamine transporter quantification . . . . . . . . . . . . . 59 59 61 Conclusions 63 1 Introduction 1.1 Background Scintigraphy is a widely used medical imaging modality for observing physiological properties in the human body. Two examples that are considered in this thesis are scintigraphic heart images and images of the basal ganglia in the brain. At the time of writing, a scintigraphic examination of the heart is at hospitals carried out by a technologist. The main tasks for the technologist is to prepare the patient for the diagnostic procedure, and later on to perform a sequence of manual operations on the acquired images. These operations includes positioning the location of the heart to a predefined area in the images, determining the orientation of the heart and concluding whereas the image quality is sufficient for the doctor to base a diagnosis on. The reorientation of the heart is necessary due to the simple fact that different individuals do not look the same; not on the outside, nor on the inside of the body. In heart scintigraphy, this presents a problem. For a doctor to give a qualitative diagnosis, the result of an examination is compared to other images. This may occur directly, by looking at different images from other patients, or indirectly, by taking into account the vast amount of images in the past that is the experience of the doctor. However, both these methods depend on the presumption that the images have been observed from the same point of view, which would not be the case if the technologist did not manually compensate for angular and rotational differences of the orientation of the heart, between different scintigraphic examinations. However, as different technologists have different experience and slightly different ways of making these adjustments, the result will not be consistent for all examinations. An automatic process for doing this would not only hopefully make the result more consistent, but also save time that the technologist has to spend on performing these tasks manually. One method for doing this has been proposed by Germano et al. [1], hoping 2 Chapter 1. Introduction to move more and more into a fully automated process [2]. However, as this method is based on intensity of the images, a more insensitive method may be desired. Moreover, scintigraphic images of the basal ganglia in the brain are beginning to be more and more popular to diagnose Parkinson’s disease. At the time of writing, quantification is used to measure a number of properties from the images of the basal ganglia, thus being able to determine the state of the patient. This process is tedious and can present difficulties if the state of the basal ganglia is poor. An automatic method for doing this quantification would benefit in much the same ways as the case with scintigraphic heart examinations. The process would be much faster compared to manual quantification, and the variability between medical staff would be eliminated. Additionally, manual quantification is performed in two dimensions and hence it could be beneficial to quantify in 3-D. Morton et al. [3] has evaluated two computer driven methods in the same field and found that a 3-D based method gives better concordance with visual assessments. 1.2 Objectives The primary aim of this project is to investigate if an automatic reorientation of threedimensional, transaxial myocardial perfusion SPECT images is possible, and if so, to design and implement an automatic segmentation method that can distinguish, and compensate for, differences in anatomical structure of the heart; particularly the angle and position of the left ventricle. The method should be able to segment and reorient the left ventricle from transaxial images into short-axis (oblique) images. Secondarily, the same method should, after little modification, be applicable to scintigraphic images of the basal ganglia. These should be segmented, and a variety of useful parameters should be extracted. These parameters should correspond to parameters that are extracted in manual quantification. 1.3 Method The work in this project has been divided into two different parts. First, the segmentation algorithm was implemented, and secondly the algorithm was applied on the two problems at hand, which first required some pre-processing in each case. ComputaR tions and simulations have been carried out with the help of M ATLAB! , version 6 and 7, from The MathWorks, Inc. The main part of the functions and methods used has been implemented with the help of M ATLAB-included primitive functions. However, to decrease computation time, a C-compiled version of convolution has been used, with courtesy of Gunnar Farnebäck at the Department of Biomedical Engineering, Linköping 1.4 Outline 3 university. To decrease the time of implementation, some functions from the M ATLAB Image Processing Toolbox have also been used. These are the bwlabel() and regionprops() for some simple morphological operations, and tformarray() for rotating 3-D volumetric objects. All the images used for development of the algorithm have been provided by Swedish hospitals. The scintigraphic heart images originate from Sahlgrenska university hospital in Gothenburg, Sweden, while the DaTSCAN-images of the basal ganglia have been provided by The university hospital of Norrland in Umeå, Sweden. 1.4 Outline Here follow a short summary of the contents of each chapter of this thesis. Chapter 2 The basics of nuclear physics is presented along with the essential parts of a nuclear medical examination. In this chapter, relevant facts about myocardial perfusion examinations and DaTSCAN examinations are also introduced. Chapter 3 In this chapter, image segmentation and registration is introduced. Some commonly used techniques are presented along with their good and poor properties. Chapter 4 The main method in this thesis, the Morphon method, is gone through in some detail in this chapter. Chapter 5 Here the problem with the estimation of angles of the heart in myocardial perfusion images is addressed with the help of the earlier presented methods and some complementary techniques. Chapter 6 This chapter involves applying the Morphon method on the problem of automatic quantification of dopamine transporters and introduces some additional tools for solving this. Chapter 7 The results of both parts of the thesis are presented in this chapter. Chapter 8 The results of the previous chapter are discussed and some future development of the methods is proposed. Chapter 9 This chapter concludes the whole thesis, its results and possible effects on the problems at hand. 4 1.5 Chapter 1. Introduction Notation This thesis inevitably involves some mathematics. The notations used are presented below. s, S v v̂ |v| M v T , MT M−1 s∗ (s1 ∗ s2 )(x) E[x] Scalar Vector Unit vector Norm of vector Matrix. Transpose of vector and matrix Inverse of matrix Complex conjugate of the complex signal s Convolution of s1 and s2 Expectation value of the stochastic variable x 2 Scintigraphy To be able to understand the process of generating scintigraphic images using nuclear medical methods such as SPECT (Single Photon Emission Computed Tomography), the basic physics behind it is laid forward in this chapter. Details on the physical aspects and more information regarding different isotopes can be found in [4] and [5, 6] respectively. 2.1 Nuclear medicine physics Nuclear physical applications in medicine have been in clinical use for many decades. The first experiments started somewhere around 1935, when Chiewitz and de Heversy [7] tested the technique on rats. At first, nuclear medicine was mainly used in therapeutical treatments, such as that of cancer, introduced by Lindgren [8]. However, as acquisition instruments and radiotracers improved, it also became a very popular way of examining physiological and anatomical properties of many parts of the human body, for example the heart [9] and the brain [10]. 2.1.1 Decay of radioactive isotopes In all imaging modalities, some kind of conceptual probe is used to gather information about the observed object at hand. This probe can be very different in different situations. For example, at an ultra sound examination, mechanical waves are used to gather information about the object, by propagation and reflection between different acoustic impedances, and in magnetic resonance imaging, radio frequency fields, interacting with fundamental properties of matter, are the probes at hand. In nuclear imaging, radiation is used to acquire information about an object. Radiation, which originates from radioactive isotopes1 . 1 An isotope of an element is a specific variation of that element, where the number of neutrons in the nucleus differ between different isotopes. 6 Chapter 2. Scintigraphy There are a variety of radioactive isotopes used in nuclear medicine. Depending on the type of examination and the region of interest in the body, the energy of the decaying particles from the isotopes has to be taken into consideration. For example, in SPECT, which is the modality of interest in this thesis, the most common isotope used is 99m Tc (technetium), which is suitable due to, among other things, its half-life and the energy of its emitted photons [11]; that is about the same as for conventional X-ray γ-energies2 . A radioactive isotope (radioisotope) is, by definition, unstable. That means that the nucleus of that element can, and will, spontaneously decay with a certain probability, given a period of time. The faster the nucleus decays, the faster will it reach its half-time value; that is when 50 percent of the amount of isotope has vanished in favour of decay radiation of some sort. There is a tremendous amount of different isotopes, both occurring naturally on Earth and synthetically produced with the help of nuclear reactions. There are also many different types of decaying processes for different types of nucleus. These different types of decay have been categorised after the type of particle emitted in the process. The most known particle emission, or radiation, is γ-radiation, where the emitted particles are photons, or light. Other common types of radiation are α-, β − - and β + -radiation [4]. β- and γ-radiation is of much interest from a nuclear medical point of view since they are the key particles in SPECT, while α-radiation is attenuated quickly in most media and is more harmful to human tissue, and therefore is used sparsely in medical diagnostics [5]. β −/+ -particles are more commonly known as electrons (e− ) and positrons3 (e+ ). 2.1.2 Detection of radiation As was stated earlier, γ- and β-radiation is preferable in nuclear medical diagnostics, however the methods for collecting images with the two methods differ. In SPECT imaging, isotopes like 99m Tc, mentioned in the first paragraph of 2.1.1, are used for different purposes. While some have been stated, the one more important for the basic principles of this imaging modality is that these kind of isotopes decay with a single emission of a γ-particle. Since the nucleus decays spontaneously, it will have an equal probability of emitting a photon in any direction [4], which is illustrated in Figure 2.1. The emitted photon will have a total energy of about 140 keV, which is suitable for many photon detectors at the time of writing [6]. To detect the emitted γ-rays, different types of detectors can be used. However, particularly in nuclear medicine scintigraphy, a common method is to use a so called scintillator for this purpose. A scintillator is basically a type of 2 The Greek letter γ is in physics often used as a symbol for photon or light. The positron is the antiparticle of the electron, which means it has exactly the same properties, except for electrical charge, which is the opposite. 3 2.1 Nuclear medicine physics 7 ! Figure 2.1: The one-step process when a radioactive isotope decays with γ-radiation. crystal4 with specific characteristics. These crystals have in common that they undergo a process called fluorescence when interacting with γ-rays of an energy matching the characteristics of the crystal. Fluorescence is a process where an element will absorb a γ-ray and immediately emit light within the visible range. This is due to the photo electric effect, where electrons in an atom can be pushed to a higher energy state and then, when falling back to the original state, send out a flash of light [4]. This light can later be amplified, for example with the help of a photomultiplier, and then detected. Guerra [6] points out that while the scintillator is more sensitive and therefore preferable in many applications, other detectors are used, such as gas-filled chambers and solid state semiconductors. 1 e+ 2 ee+ ! Figure 2.2: The two-step process when a radioactive isotope decays with a positron (β-decay), which shortly thereafter reacts with an electron, creating γ-radiation. While single photon emitters (SPE) such as 99m Tc are used to detect one γ-ray at a time, 4 Common crystals that are used in nuclear medicine are: Cerium doped lutetium orthosilicate (LSO), cerium doped gadolinium orthosilicate (GSO) or yttrium aluminium perovskite (YAP) [6]. 8 Chapter 2. Scintigraphy there is another method used in nuclear medicine that utilise positron emitters (PE), such as Oxygen-15. In accordance to the name, positron emitters decay by emitting positrons; that is with β + -decay (see figure 2.2) [5]. However, as an antiparticle to the electron, the positron will readily react with electrons it encounters, annihilating both particles and sending out two photons near exactly in the opposite direction to each other. In vivo, the positron will react almost instantly with an electron, producing two photons that will radiate from the same source [4]. Consequently, even though another type of nuclear decay is the source of radiation, photons will, in the end, be detected by both type of radioisotopes. In nuclear medicine, the imaging modality using PE is referred to as PET (Positron Emission Tomography). PET-images are very similar to SPECT-images, but they will not be studied any further in this thesis due to the lack of PET-image material. 2.2 Single Photon Emission Computed Tomography The imaging modality that is the source of all images in this thesis is SPECT. In SPECT, photons from single photon emitters are detected in a manner as described in 2.1.2. SPECT is a widely used modality and has been used for some time. One of the great advantages of SPECT compared to projectional modalities like X-ray imaging is its ability to acquire images in 3-D, thereof the word tomography in the abbreviation. Larsson [12] presented one of the first working tomographic systems and the image quality has been much improved ever since. 2.2.1 Image quality What should be mentioned about the images generated in a SPECT examination is that they are low in resolution and signal to noise ratio compared to images from other imaging modalities, such as CT (computed tomography) and MRI (magnetic resonance imaging). A typical SPECT-image has a resolution of 643 voxels5 , while the other modalities can have resolutions of 5123 voxels and above [5]. The low resolution in SPECT-images originates from the fact that the photon count, i.e. the number of photons that are detected, is quite low and that SPECT registers physiological processes in the body, not anatomical structures as CT and MRI are mainly used for. Further more, even though the photon count could probably be increased with a more radiating radioisotope, it would consequently increase the dose of radiation applied to the patient. 5 The three-dimensional correspondence to an image pixel. 2.3 Scintigraphic examinations 2.3 9 Scintigraphic examinations There are many steps involved in a clinical scintigraphic examination. In this section, the process of examining myocardial perfusion as well as dopamine activity in the basal ganglia, and some problems that arrises with manual diagnoses in such examinations, will be presented. In most nuclear medical applications the radioisotope that generates the image signal is tagged to a compound of some sort, called a pharmaceutical agent, which is injected into the patient. Together, the isotope and the agent are named a radiotracer, which is used to attach itself to the organ that is to be investigated, and to make the radioisotope less hostile to the body. For example, as exemplified by Wilson et al. [13], in myocardial perfusion SPECT examinations, tert-butyl is commonly used, and for the brain images studied in this thesis, the popular DaTSCANTM radiotracer from GE Healthcare [14] has been used. 2.3.1 Myocardial perfusion SPECT Myocardial perfusion SPECT examinations are widely used as a routine examination for patients with chest pain. Some time after the technologist has injected the radiotracer into the patient, he/she will be placed in a camera station, often referred to as γ-camera, with a detector suitable for SPECT γ-energies [6]. After the camera has finished with the acquisition the image is reconstructed using some reconstruction technique, e.g. as proposed by Perkins [5]; filtered back-projection or iterative reconstruction. This will Figure 2.3: A 3-D volume image displayed as iso-surfaces (left) and two slices (center and right), with the left ventricle of the heart marked with an arrow. yield the images, which are tomographic 3-D volume data, i.e. each voxel in space has three space-coordinates (x, y, z) as well as an intensity level. In practice, the 3-D volume consists of a number of slices. This makes it convenient to display the volume in the form of a stack of 2-D images, which is often used clinically. Strauss and Miller 10 Chapter 2. Scintigraphy [15] describes the procedure in more detail. An example of a 3-D volume acquired using SPECT can be found in Figure 2.3. The next task for the technologist is to rotate the acquired images of the heart into predefined angles. This is done by choosing two slices from the volume, which the technologist finds good for estimating the angle of the heart [15]. An example is given in Figure 2.4. Figure 2.4: The manual rotation of the heart performed by the technologist. The heart is here illustrated before (first row) and after (second row) rotation, for slices through each axis respectively. It is obvious that the centre line of the left ventricle, which is commonly seen as the line that should align with the axes after rotation [15], cannot be exactly defined for such an asymmetrical object as the left ventricle. Even more so when the images acquired are of poor quality, or if the uptake of radiotracer in the left ventricle is poor, due to, e.g., myocardial infarction. This poses a problem for myocardial perfusion SPECT images, and is discussed in this thesis. 2.3.2 DaTSCAN Quantification DaTSCAN quantification is another SPECT-application that is very commonly used to diagnose Parkinson’s disease. If a patient suffers from Perkinson’s disease, the basal ganglia are often degenerated, i.e. the number of dopamine receptors are reduced. Moreover, the degeneration is generally first observed from the same place of the ganglia. However, the quantification methods that are used introduces great inter- and intraoperator variability, which is discussed by Tatsch et al. [16]. Often, a two-dimensional quantification method with predefined or adjustable regions of interest (ROI) is used, 2.4 Summary 11 which requires operator interaction throughout the whole quantification process. Visual interpretation of the images are also common, which introduces even more sources of error, e.g. the use of different colour maps; noted in [16] as: Use of non-continuous color tables may overestimate findings due to abrupt color changes. Tatsch et al. [16] As with myocardial perfusion SPECT images (section 2.3.1), the variability is great between different images. An example of how the basal ganglia are manually quantified is given in Figure 2.5, where a typical ROI has been drawn around each of the basal ganglia, as well as for the background signal of the image. The quantification of the Figure 2.5: Illustrating a typical ROI of the basal ganglia and background area (4) of a manually quantified DaTSCAN-image. images is commonly based on measuring the signal inside the ROI (or different parts of it) of the basal ganglia, and comparing it to some kind of background signal. The background signal has traditionally, with 2-D quantification, been chosen as the visual cortex (see nr. 4 in Figure 2.5), but there is no absolute standard [16]. The quantification procedure can take a significant amount of time for an inexperienced operator and there is little standardisation in the way that the different ROI:s are selected and adjusted. 2.4 Summary After this chapter, the reader should be sufficiently informed on how SPECT-imaging works, both theoretically, physically and on a more practical level, which has been exemplified with the two applications that are involved in this thesis; myocardial perfusion 12 Chapter 2. Scintigraphy SPECT and DaTSCAN quantification. Problems that both applications have in common regarding inter- and intraoperator variability as well as dimensional reduction approximations from 3-D to 2-D, have also been introduced. 3 Image Segmentation Image segmentation is in principle a method for bringing out certain, more interesting, parts of a signal, and has been used in medical applications for many years. The signal may for example consist of a two dimensional image, or as in the case of this thesis, a three dimensional volume. Both cases are common situations in medical informatics. In this chapter, a brief overview of common image segmentation techniques will be covered, and since the principles are the same for signals of different dimension, examples will mainly concern two dimensional images, since they are easier to visualise. Image segmentation in more detail can be found in [17]. 3.1 Segmentation methods There are many different image segmentation methods. From the very simple and intuitive, to techniques based on advanced mathematical concepts. An important issue to consider is therefore what type of segmentation method to apply, given a certain situation. This often depends on the image modality used to acquire the image, as well as the complexity of the part of the image that is to be segmented. 3.1.1 Thresholding In a very simple and clear image, simple and intuitive segmentation methods can often be sufficient. In such images, with a good signal to noise ratio, so called thresholding is often a good choice. Segmentation by thresholding works simply by keeping the part (pixels/voxels) of the image that lies in a certain intensity interval. This is demonstrated in Figure 3.1 b), where the pixels above a certain intensity level in the original image has been set to 1, and the rest of the image to 0, and can also be described mathematically 14 Chapter 3. Image Segmentation with Isegmented ! 1, a < I < b = , 0, o.w. (3.1) where I is the original image and a and b are the thresholds. However, if the image signal is bad and mixed with noise, thresholding will often yield a bad result. This is shown in Figure 3.1 c, where noise has been added to the original image. Figure 3.1: a) (left): An X-ray image of the hand of Wilhelm Röntgen’s wife. b) (centre): The image after thresholding. c) (right): The image after thresholding where noise has been added to the original image. Furthermore, another problem with thresholding is choosing a good threshold level that is not specific to one image. This can be done by for example examining the histogram of the image, or by other more or less sophisticated guesses. At last, segmentation by thresholding is often not a good choice where the interesting parts of an image has the same intensity levels as the rest of the image, and is only separated by structure and shape. In such situations, some kind of image registration is often required for good results. 3.1.2 Region growing A segmentation method that resembles thresholding is region growing [17]. However, in contrast to thresholding, which operates on each point in an image independently of neighbouring points, region growing takes into account the surrounding connected pixels. Region growing requires a starting point in the image. This point should be a known point within the area of interest, and consequently the method requires manual 3.2 Image registration 15 input or some kind of pre-processing. When the point is chosen, the method works iteratively. A neighbouring point is chosen. If the intensity of that point is within a certain intensity level from the starting point, the point is considered part of the final segmentation, and the process starts over, now starting at this point. There are several more or less advanced techniques for implementing region growing, however, it often gets very slow with higher image dimensions. More over, region growing can in its basic form handle images with much noise very poorly. There are ways of reducing noise, but nevertheless, region growing will not take into account the structure of the interesting parts of an image and is highly dependent on image intensity. 3.1.3 Active shapes The thought behind active shapes takes region growing a step further by introducing prior knowledge of the the object that is to be segmented. The goal in active shapes is to find a line in 2-D or surface in 3-D, that encloses the object of interest after segmentation. Active shapes works by first defining a model. The model is built from a data set of other images of the same kind of object that is going to be segmented. In each one of the images in the data set, the same landmarks (often anatomical) have been marked. By observing how the position of the landmarks differ throughout the data set, the variance of each landmark can be calculated [17]. In turn, this is used to define how the model is allowed to move while it is segmented. The actual deformation of the model can be generated in various ways. One common way is to use the energy in the image to calculate edges and borders, to where the model should deform. Compared to region growing techniques, active shapes are much more robust and insensitive to noise. This is due to the prior knowledge introduced about the object, which prevents the model from deforming in an unnatural way. The constraint of active shapes is off course the data set. If the data set is small, the model will not be able to deform sufficiently when introduced to cases that are not represented in the data set. However, with a large data set, active shapes is often a good method in more complicated segmentation situations. 3.2 Image registration In many situations, particularly in medical imaging, simple segmentation methods such as thresholding is not sufficient to yield good results. The segmentation process can then often be helped by adding image registration to the segmentation process. Image registration is in principle a method for deforming one image to align to another image. In medical informatics this is often used to map one image, with one type of information, to another image, containing other types of information. One example is to map an image of a brain acquired with computed tomography (CT) or magnetic resonance 16 Chapter 3. Image Segmentation imaging (MRI) to another image of the same brain, acquired with SPECT. Since the brain may not be in the same position at both times of examination, image registration is used to make the same areas of the two images correspond to the same areas of the brain. In this example, information about the anatomy of the brain, in the CT or MRI images, will then be complemented with physiological information from the SPECT image. Mathematically, image registration can be described by finding a deformation field, or a displacement field, v(x), that after acting on an image, I2 (x) will deform the image in such a way that it will map to the target image1 , I1 (x). The mapping in n dimensions can be described by v(x) : Rn "→ Rn . (3.2) Moreover, to be able to describe the quality of the registration process, the error $2 = $I2 (x + v(x)) − I1 (x)$2 (3.3) is introduced. If this error is zero, the registration process has been completely successful. This is not a realistic goal in practice, since the two images do not contain exactly the same information, in which case image registration would not be necessary. Consequently, v(x) describes how each point in I2 should be moved to minimise $. There are many attempts of solving this problem, and many involve minimising some variation of a least square problem. For example, if the following assumptions are made: 1. v(x) can locally be described solely by a spatial displacement. I(x, t) = I(x + ∆x, t + 1), (3.4) where t denotes the time in the discrete registration process. 2. The image can in each point be approximated with a first order Taylor expansion. I(x + v(x), t + 1) = I(x, t + 1) + ∇I T v, ∇I = [∂I/∂x, ∂I/∂y]T . (3.5) If equations (3.4) and (3.5) are combined, the equation for the so called optical flow, denoted by v, can be found. ∇I T v − ∆t = 0, ∆t = I(x, t) − I(x, t + 1). (3.6) Optical flow is one of the oldest concepts in image registration and computer vision and a lot of research has been done around it. Consequently, there are many methods for 1 Target image is usually the name of the image that is left untouched. 3.3 Summary 17 solving the differential equation (3.6). As a matter of fact, there are many solutions for v in each point in the image; solutions that are not practically usable, since image points can then have completely independent solutions of each other. This is described in more detail in [17], chapter 6:6. However, one robust solution that consider the optical flow as a continuous function is a least square problem formulation: " $2 = ([∇I(xi )]T v(xi ) − ∆t (xi )) (3.7) i By assuming different properties for v in equation (3.7), different types of solutions for the displacement field can be found, with different amount of rigidity [18]. For example, in some situations a mere translation or rotation of v is a good enough registration model, while in other more complex applications, a non-rigid model must be used, which allows for any kind of deformation of I2 . The parameterized solutions for different levels of rigidity can be found in [17]. In this section, the optical flow was found through differences in the intensity of images. While straightforward, this approach is obviously dependent on the assumption in (3.4). There are, however, other more robust procedures for estimating the optical flow in a registration process between two images. Differences in local phase is one such approach, and will be described in more detail in chapter 4. 3.3 Summary In this chapter, an overview of more and less advanced segmentation methods have been presented. From thresholding, which is easy to understand and implement, to registration based methods; derived within a rich mathematical framework and still issue to much research and algorithm optimisation. 4 The Morphon Method The Morphon method is a newly developed method for image segmentation and registration, first introduced by Knutsson and Andersson [19]. Since then, the method has been under refinement and have been applied in several medical applications [20, 21, 22, 23]. This chapter is mainly an overview of the Morphon method, based on [19] and [20]. The method can be brought to a much more advanced level, nevertheless, this simplified (and hopefully faster) version is sufficient for the subject of this thesis. The Morphon method is essentially a registration driven segmentation technique. It works by first estimating a displacement field through differences in local phase between the segmentation target image and a model image, which resembles the target image in e.g. intensity variations. The displacement field is further processed to ensure robustness of the method. The model of the object that is to be segmented is deformed according to the displacement field, and the whole process is iterated until the process is satisfactory and the model has mapped on to the target image. In the beginning of the work of this thesis, a method for solving the stated problem in a satisfactory way had not yet been proposed. After investigating several image segmentation and registration methods, the conclusion was finally that a phase based approach such as the Morphon method had several advantages in comparison, given the problematics of this project. The primary reasons for choosing the Morphon method can be summarised with the following arguments. 1. Phase: As mentioned in section 3.2, a phase based approach on image registration can be advantageous compared to classical techniques with intensity based optical flow estimation. Even more so in the images that is considered in this thesis. Section 2.3.1 shows that SPECT images of the heart can vary considerably in intensity. Not only among different images, but also between the heart and other organs. In such situations, intensity based techniques are inferior to a method such as the Morphon, which, as presented in 4.1.1, is insensitive to intensity variations. 20 Chapter 4. The Morphon Method 2. Noise: If the images are of low quality1 , which is not an unusual case with SPECT images (see section 2.2.1), assumption 2 (equation (3.5) might very well not hold. However, the Morphon method uses robust methods such as displacement field accumulation and regularisation to prevent the displacement field from diverging. 3. Model: The Morphon framework includes an easy and dynamic way for including prior knowledge about the object that is to be segmented. This makes it easy to develop further for other applications, as will be presented in chapter 7, Segmentation and quantification of DaTSCAN images. 4.1 Displacement field estimation A displacement field is essentially a vector field. In this approach, the field is dense, which means that in each point in space, there exists a vector with a certain direction and magnitude. Since the image space is discretised with pixels or voxels, the vector field will have the same size as the image that is to be deformed by it. There are, however, other applications, where the deformation field is not dense, and a vector describes the movement of a block of discrete points. To estimate a displacement field in the Morphon method, analysis of the local phase of the images is made. 4.1.1 Quadrature phase Phase can principally be described as the structure of the image. Mathematically, the phase, as it is used in this thesis, is the response from a certain set of filters that respond to edges and borders in the image. These filters are known as quadrature filters and are defined as follows. Quadrature filter 4.1.1. A filter, f (x), is a quadrature filter if its Fourier transform, F (ω), is zero on one side of a hyper plane through the origin in the Fourier domain. That is, there exists a vector, n̂, such that ! 0, n̂T ω ≤ 0 F (ω) = . (4.1) F (ω), o.w. In this thesis, one special type of quadrature filters have been used, namely lognormal2 filters, which are described, for example in [24], in the Fourier domain as 4 F (ω) = e− B2 ln2 ln 1 2( ω ) ωc (4.2) Quality can be hard to define. Here, quality mainly refers to signal-to-noise ratio and the amount of artifacts. 2 Lognormal filters are often referred to as lognorm filters. 4.1 Displacement field estimation 21 for positive values of ω. Here, B is the relative bandwidth of the filter in octaves and ω c is the centre frequency of F (ω). In Figure 4.1, a lognorm filter is shown in the spatial and frequency domain. For displaying reasons it is shown for only 1 dimension, but the principle is the same for arbitrary dimensions. Due to the quadrature filter definition in the frequency domain, quadrature filters are always complex in the spatial domain. This can be understood since F (ω) '= F (−ω), (4.3) F (ω) = F (−ω). (4.4) while a necessary requirement for f (x) to be real is that !&#" # '()* +,)-./)01 $%+ !&# $%* $%) !&!" $%( $%' ! $%& $%! !!&!" $%" $%# !!&# ! " #! #" $! $" %! $ !! !" !# $ # " ! Figure 4.1: Lognormal filter with real and imaginary parts in the spatial domain (left) and the Fourier domain (right) In computational practice, filters are discrete, and it is often desirable to adjust the finite length of the quadrature filter. A smaller filter will imply less computations while making calculations with the filter. Moreover, the size of the filter will have impact on the size of the items that the filter is able to detect. The size of the filter can, and will, therefore depend on the application at hand. A good way to design a filter kernel, that introduces much control over the filter properties, is suggested by Knutsson et al. [25] and is based on a least square formulation of the filter design problem. The main idea is to introduce a number of ideal filters in each domain where they can be easily described. Here the quadrature filter has been defined in the Fourier domain (4.1.1), which is suitable for this technique. However, it is also desirable to achieve a filter which is small in the spatial domain, i.e. ideally resembling δ(x), an impulse3 . In short, the problem can be formulated as " $2 = $Wj (fj$ − Bj f )$2 , (4.5) j 3 Mathematically known as the Dirac delta function. 22 Chapter 4. The Morphon Method where f is the desired filter in the spatial domain, Bj is the base matrix that when multiplied by f will give f described in domain i, and fj$ is the ideal filter for domain i. Wj is a weight matrix which can be used to make certain parts of the filter more important, i.e. more sensitive to errors. For this case, the only domain other than the spatial is the Fourier domain. Thus, Bj will here either be the Fourier base matrix or the unity matrix. In each case respectively, Bj f will give F (ω) and f . As mentioned above, the phase, φ, of a signal, s(x), is related to the response from these filters. More specifically, phase can be defined as the angle of the filter response between the signal and the filter, derived from q(x) = (s ∗ f )(x), (4.6) where q is the filter response and ∗ denotes the convolution operator. Assuming s(x) is real valued4 , q is complex and can be rewritten on polar form as q(x) = A(x)eiφ(x) . (4.7) Here A(x) is the magnitude of the filter response, and the phase can now be found through φ(x) = arg(q(x)). (4.8) Finally, what is left is to generate a displacement field from the phase of two images. Assuming the two images I1 and I2 , we get two different responses from the same set of filters. Since lognorm filters, from definition 4.1.1, are dependant on the direction of n̂, we actually get one response from each filter in the filter set. A filter set can consist of as many filters wanted, however, there is a minimum of filters needed given a certain dimension of the images to be able to cover the whole Fourier domain. This is due to the fact that the filters have a direction and a limited spread. For example, in two dimensions, at least three filters are needed and in three dimensions, six filters is the minimum to span over the whole domain. This is discussed in more detail for example in [26]. The six directions for 3-D given in [26], for a second order filter, and which are used in this thesis, are n̂1 n̂2 n̂3 n̂4 n̂5 n̂6 4 = c[b, −a, 0]T = c[b, a, 0]T = c[0, b, −a]T , = c[0, b, a]T = c[−a, 0, b]T = c[a, 0, b]T The signal in this context is a two or three dimensional image, which in most circumstances is real valued. 4.1 Displacement field estimation a = 2, b=1+ √ 5, c= 23 # √ 10 + 2 5, where a, b and c is only for normalisation. From above, it is therefore necessary to apply convolution between the signal and all the n number of filters in the filter set. This leads to n filter responses for each image, each one representing the phase and magnitude in the direction of filter j (see Figure 4.2 for an example), i.e. (4.9) qj = (s ∗ fj )(x). From this we have one response from I1 and one from I2 for each filter in the filter set: Figure 4.2: The original X-ray hand (left) along with the phase (centre) and magnitude (right) of it after being filtered with a quadrature filter. Here it is seen that the filter captures edges corresponding to the filter direction, giving more certainty (magnitude) to structures with a frequency within the passband of the filter. qj (I1 ) = (I1 ∗ fj )(x), qj (I2 ) = (I2 ∗ fj )(x). (4.10) Further more, the phase difference at position x between the images can be found through the product between qi, I1 and the conjugate of qi, I2 , or qj (I1 )qj∗ (I2 ) = Aj (I1 (x))Aj (I2 (x))ei(φj (I1 )−φj (I2 )) . (4.11) From this, the phase difference is, analogue to equation (4.8), equal to ∆φi = arg(qj (I1 )qj∗ (I2 )) = φj (I1 ) − φj (I2 ). (4.12) dj (x) ∝ ∆φj . (4.13) Since this is the difference between the images, it is also locally proportional to the displacement field estimate at that point: Moreover, what we now have is a set of n displacement field estimates, each one representing the estimate in direction i. 24 Chapter 4. The Morphon Method 4.1.2 Least square solution To bring the information from each one of the estimates together into one displacement field estimate, a least square problem is a suitable way of postulating this problem. Since least square problems have the great advantage of being able to weight different points with different importance, as is common in filter design, for example described in [25], this can also be used for the derivation of the total displacement field. In this case, the weight function is called the certainty of the filter responses and is defined as cj = Aj (I1 (x))Aj (I2 (x)). (4.14) The certainty will then be high where the two filter responses match each other in structure, which is sensible, and this makes for all the parts in the least square problem to calculate the whole displacement field, d = (d1 , . . . , dN ), for N dimensions. " min [cj (n̂Tj d − dj )]2 , (4.15) d j for each direction, n̂j . Further more, since the Morphon method is an iterative registration scheme, the displacement field estimate is only valid for the current iteration, and must be updated with each iteration, thus generating a new field, dk , for iteration k, which brings us to a central part of the Morphon method. 4.2 Displacement field accumulation As presented above, each iteration generates a new displacement field, solved from equation (4.15). However, the field for iteration k might not be a good estimate compared to estimates prior to that iteration. To prevent bad estimates to disrupt the registration process, a field accumulation is therefore used to make good estimates gain greater influence on the final displacement field. The accumulation also have another effect on the registration process as it prevents interpolation smoothing to be spread throughout the iterations. Since the model (I2 here) has to be deformed in each iteration and a new displacement found from the deformed model, smoothing would occur if dk would be applied directly on the model for each iteration. Instead, the newly found field is added to the field found and accumulated in iterations before, removing interpolation artefacts since the original model is now used for each iteration. The accumulated displacement field is updated through d$a = ca da + ck (da + dk ) , ca + ck (4.16) 4.3 Displacement field regularisation 25 where da denotes the accumulated field for the current iteration and d$a is the next, updated accumulated field. ca and ck both describes certainty measures, associated with the ones mentioned in equation (4.14). ck is directly coupled with the displacement estimate for each iteration, dk , and is defined as ck = n " cj , (4.17) j i.e. the sum of all certainty measures for each quadrature filter. ca , on the other hand, is another accumulated entity and is a certainty measure weighted with its own certainty, expressed as c$a = c2a + c2k , ca + ck (4.18) where c$a , analogue with above, is the updated certainty measure. To summarise; the accumulation of the displacement field implies that good displacement field estimates will have a higher effect on the accumulated (final) displacement field than poor ones. This creates a robustness of the algorithm as well as increases its reliability. 4.3 Displacement field regularisation As mentioned in section 4.1.1 about quadrature phase of images, the phase is only a local description of the image. If the accumulated field estimates from equation (4.16) were to be directly applied to the model image, it would most likely tear the image apart, diverging into something far from a successful registration operation. However, since the field represents local changes in the image, it is sensible to think that an averaging of sorts would represent a change on a more global scale. This averaging can be made more or less complicated. Often, it is done by means of a basic Gaussian averaging: dr = (d ∗ g)(x), (4.19) where g is a Gaussian kernel and dr is the regularised field, but can be made more advanced in many ways. In this thesis, a special form of normalized convolution, as first introduced by Knutsson and Westin [27], called normalized averaging, is used. Normalized averaging introduces the great advantage of allowing to include the certainty measure in the regularisation process as well, adding even more robustness and reliability to the registration. Normalized averaging is defined as dr = ((ca d) ∗ g)(x) , (ca ∗ g)(x) (4.20) where the division and multiplication are taken element wise. The effect of a small and a large standard deviation of a Gaussian kernel is presented in Figure 4.3. 26 Chapter 4. The Morphon Method Figure 4.3: A displacement field during a Morphon registration process with a small (left) and large (right) regularisation of the field. 4.4 The model The model in the Morphon method is the image that is deformed by the displacement field, and hence contains the information about the registered object after the registration has finished. However, to perform a successful registration, an appropriate model is needed. The type of model often depends on the context or problem. Nevertheless, a good model should contain approximately the same information regarding shape and intensity variations as the target object. For example, in this thesis segmentation is performed on SPECT images of the heart. A suitable model could therefore reside in a manually segmented heart from another SPECT image. 4.4.1 Deformation The model is deformed, using a suitable interpolation method, by the accumulated displacement field at the end of each iteration and the deformed model is used to generate the new accumulated deformation field, which in turn deforms the original model. This is iterated until some kind of accuracy, δ, or a maximum number of iterations is reached. The accuracy could for example be the change of the accumulated displacement field between two, in the iteration process, adjacent fields, i.e. $ $ $ dr, k − dr, k−1 $ $, $ δ=$ $ dr, k where the relative difference has been chosen as the accuracy. (4.21) 4.5 Summary 4.5 27 Summary Here, a simpler version of the Morphon method has been described in some depth. The method takes advantage in its local phase based registration scheme, which is iterated through different resolutions. A displacement field is found for each iteration and is accumulated and regularised to make the registration more robust, as well as adding the option to make the model more or less rigid and deformable. 5 Rotation of Myocardial Perfusion Images As presented in section 2.3.1, there are some problems with the image analysis in scintigraphic heart examinations as they are carried out at the time of writing this thesis. The main problems are: • Interoperator and intraoperator inconsistency, that ends in difficulties in comparing images acquired from different technologists, or even from from the same technologist. • Time consuming activities for the technologist after images have been acquired. • Difficulties in manual alignment for images with poor uptake. The approach in this thesis for designing an automatic method for doing all this is based on the Morphon from chapter 4. The automatic process involves some pre-processing, to help the later registration scheme, followed by a 2-D registration and segmentation to decrease the amount of data. After this, the 3-D image should have been decreased to a small volume, containing the left ventricle of the heart. A 3-D Morphon is then applied to the image, from which a displacement field is generated. This displacement field, with enough regularisation, is a rough description of how the model have been rigidly transformed to match the target image. By estimating the angle with the help of two lines, the rotation of the left ventricle can be known, and the target image rotated correctly. The sequence is in this chapter described in detail. 5.1 Pre-processing of images The first problem in this application that must be dealt with is that the amount of data has to be decreased, in order to increase performance of the analysis. This is primary done in a quite primitive way by cropping the 3-D image along all of its dimensions. The cropping assumes that the technologist has placed the patient correctly in the γ- 30 Chapter 5. Rotation of Myocardial Perfusion Images camera and that the heart is not positioned in the right side of the body. The cropping is illustrated in Figure 5.1. Figure 5.1: The pre-cropping that will help the registration process. To the left, the original image, and to the right the cropped image. The left ventricle is marked with a black rectangle in both images. 5.2 2-D Morphon segmentation After the image has been cropped, the first Morphon based segmentation is performed. As this is a 2-D segmentation, the 3-D volume must first be reduced. This is done by transforming the volume into a max intensity projection (MIP) image, i.e. by generating a 2-D image where each pixel is the maximum of all the voxels that after a projection would result in that pixel. This is performed along the y-axis, which is the axis in the same direction as the nose of the patient, or that is pointing out from the patient’s chest. This is illustrated in Figure 5.2 a). Figure 5.2: a) Maximum intensity projection along the y-axis (green). b) Maximum intensity projection along the x-axis (red). The resulting projections are symbolised by the purple plane. 5.2 2-D Morphon segmentation 5.2.1 31 Locating the heart Since other organs can have very similar shape and intensity variation compared to the left ventricle of the heart, it is important to help the registration as much as possible. This is done by finding a point of the heart where the Morphon can be initiated. By assuming that there are only uptake in form of noise in the parts above (in the negative z-direction, which is symbolised by the blue vector in Figure 5.2) the heart, a thresholding can be performed to remove any noise, after which the heart should contain the lowest point in the z-direction. This assumption has been made after investigating a great number of images (over 600). As presented in section 3.1.1, the threshold level can be found in different ways. Here, a dynamic way is needed to keep the thresholding from removing the heart completely. This is done by calculating the histogram of the image. This will result in a curve with some maxima and minima, where the maxima are a representation of intensity levels that are more common in the image. As this do not apply to noise to the same extent, a suitable threshold level that contains the heart can be found. However, this may not be enough if the noise level is very high. In order to separate noise from the heart, the size of the binary clusters that are found is calculated. If the size is too small, it is likely that it does not represent the heart. Additionally, a distance test is performed. This test calculates the distance from the centre of mass (COM) of the image and the point that has been found, where the COM is defined as % I(xi )xi %i , ∀i, (5.1) i I(xi ) for a pixel at position xi with intensity level I(xi ). As the intensity levels in the MIP image are much higher in the lower parts of the body, it is there that the COM will be found. The distance from the COM to the heart is therefore relatively short, and points that are found too far away from the COM can be regarded as noise. 5.2.2 Segmentation When a point of the heart has been found, the 2-D Morphon can be initiated and performed. The model used is a MIP image from another heart, which represents the intensity variations in a suitable way. Moreover, as the model may still, despite the tests from above, be initiated quite far from the heart, the registration is first performed on a lower scale of the image (naturally, with a down sampled model as well). Still, the same size of the quadrature filters is used, which implies that the model will "see" longer than on full scale. To perform the registration on different scales is a good way of preventing the registration to converge locally on details, before it has reached the heart. When the model has converged, it should be known where the heart is situated in the 2-D MIP-image. It can then be cut out along the third dimensions, resulting in a 32 Chapter 5. Rotation of Myocardial Perfusion Images Figure 5.3: The result after two 2-D Morphon segmentations. cylinder like volume which is oriented along the axis of the maximum intensity projection (y in this case). The resulting volume is then made a MIP along the x-axis, which is illustrated in Figure 5.2 b), and another 2-D Morphon is initiated. However, as much of the interfering organs around the heart has been cut away already, it is sufficient to initiate the model at the COM of the MIP image, which will result in a good registration. Consequently, when the registration has converged, even more can be cut away in the same manner as above. The result is a relatively small box, containing the heart and possibly other organs that lies very close to the heart. An example of the result can be seen in Figure 5.3. 5.3 3-D Morphon segmentation From the segmentation covered in the last section, the heart is now separated from the majority of interfering organs. The last segmentation process is now made in three dimensions to be able to gather information about the orientation of the heart. As the co-ordinates of a point that is known to have its position somewhere in the heart, this point is a sensible starting point for the model in the 3-D Morphon registration. However, as the starting point will probably not correspond exactly to the same point in the model, the 3-D registration is here as well performed in multiple resolutions. The reg- 5.4 Angling of the heart 33 ularisation of the displacement field is relatively large on the lower scales to keep the model from deforming incorrectly in the absence of the details of higher resolutions. At full resolution, on the other hand, the standard deviation of the regularisation filter is relatively smaller. This means that the model can deform into more detail, which is necessary due to the great variation between images from scintigraphic heart examinations. The model in the 3-D segmentation is as in the 2-D case a manually segmented 3D heart. The model will deform significantly between different types of hearts. An example of this is illustrated in Figure 5.4. Figure 5.4: The original model (top-left) and three examples of it after being deformed in the registration process. 5.4 Angling of the heart After the 3-D Morphon registration has converged, the model should have aligned itself to the left ventricle of the heart. The model can then be used to segment the left ventricle, which is one of the aims of this thesis. Moreover, the rotation of the heart requires some thought on how to represent the rotation of the model. 34 5.4.1 Chapter 5. Rotation of Myocardial Perfusion Images Angle estimation To represent an angle between two objects, a minimum of two lines is needed. The first line has been manually defined from the original model. The line does not need to be represented by voxel coordinates in the image, but can be mathematically defined as desired. Here, the line is situated in the middle of the left ventricle, in the cavity called the lumen, and has a length that does not exceed the length of the heart in the same direction. Mathematically, the line can be expressed as x0 vx x0 + tv = y0 + t vy , z0 vz t = 0 : l, (5.2) where x is the starting coordinate of the line, v is the unit direction vector and t is a parameter which determines the length, l, of the line. The deformation field that has been found through the 3-D registration can now be used to deform the line accordingly. However, as a small regularisation has been used on the full scale registration, the line is likely to be deformed into a discrete curve. This is not desirable and hence the field is further regularised. With a large regularisation filter, the global displacement will more and more correspond to a rigid transformation field. However, the deformed line will nonetheless become slightly bent. This is solved by fitting a line to the deformed points of the line, resulting in a linear regression problem: min α, β " i [zi − (αxi + β)]2 , x = (x, y), (5.3) with parameters α and β, or min $Ax̃ − b$, x̃ (5.4) where A is a known basis matrix, x̃ is an unknown parameter vector (here, containing α and β) and b is a known vector containing the function values (here, the z-axis). From linear algebra we know that the solution for a least square problem is: x̂ = (AT A)−1 AT b. (5.5) This will yield a straight line that has been approximately rigidly transformed from the original line, and the angle, θ, for each axis respectively can be calculated from the definition of the scalar product between two vectors, u and v, given as uT v = |u||v|cosθ. (5.6) 5.5 Summary 5.4.2 35 Rotation As the angles of rotation around each axis have now been estimated, the remaining task is to rotate the image heart with the corresponding angles. This can be done in a multitude of ways, e.g. applying a rigid rotation matrix and interpolating the image to the new position. The segmented and rotated heart can then be displayed in any way desired, however, the common clinical way is in slices through each axis. An example of a segmented heart, before and after rotation, can be found in Figure 5.5, where a surface of the volume object is displayed, and in Figure 5.6, where one slice through each axis is shown. Figure 5.5: Iso-surface plot of an automatically segmented heart (left) and the same heart after rotation (right). Figure 5.6: Three slices through the rotated heart as they are commonly displayed in clinical use. 5.5 Summary The segmentation and alignment of myocardial SPECT-images is performed with the aid of two 2-D and one 3-D registrations, based on the Morphon method from chapter 4. The angles are consequently found through deforming a line along with the deformation of the model in the method. 6 Dopamine Transporter Quantification From section 2.3.2, it is clear that there are currently some problems involved in quantification of 3-D scintigraphic brain images which aims at diagnosing e.g. Parkinson’s disease. This relies both in the variability between operators and the fact that much quantification is made in two dimensions, while the acquired images are in fact in 3-D. Thus, The 3-D segmentation method used in chapter 5 has been somewhat modified and complemented, and then applied on the quantification problem at hand. The algorithm for automatic 3-D quantification works by first dividing the SPECT-brain image into two parts and quantifying each part individually. This is followed by an initiation of the 3-D Morphon segmentation process. The segmented basal ganglia are then further analysed and quantified with methods comparable to the manual 2-D quantification commonly used clinically. To be able to do this, a method called weighted principal component analysis (wPCA) is introduced. 6.1 3-D Morphon segmentation Compared to the segmentation process of the heart in chapter 5, specifically section 5.3, very little pre-processing is necessary in the case of DaTSCAN SPECT images. In myocardial perfusion SPECT images, the image signal from the left ventricle of the heart constitutes a small part of the total image signal. This is in contrast to DaTSCAN SPECT images of the brain, where the basal ganglia (the region of interest) stand out in a much clearer way. This is illustrated in Figure 6.1. Consequently, the initiation of the 3-D segmentation can be greatly simplified compared to the pre-processing in chapter 5; e.g. the two 2-D segmentations from section 5.2.2. 38 Chapter 6. Dopamine Transporter Quantification Figure 6.1: Two iso-plots of a myocardial perfusion SPECT image (left) and a DaTSCAN SPECT image (right). The left ventricle is marked with an arrow and the basal ganglia are the red bean-shaped objects. 6.1.1 Locating the basal ganglia As mentioned above, the brain image is first divided into two halves, each containing at least one whole basal ganglia. The division is simply done by examining the intensity profile through the axis going through both of the basal ganglia and dividing the volume at the minimum between the two maxima, as illustrated in Figure 6.2. This makes it pos4 x 10 4.5 4 Intensiity 3.5 3 2.5 2 1.5 1 5 10 15 20 25 Position 30 35 40 Figure 6.2: The intensity profile of the brain (left), with marked local maxima and local minimum, taken along the x-axis, shown to the right. sible to divide the brain in approximately the two brain halves, each image containing one basal ganglia. Further more, since the basal ganglia in almost all cases have a significantly higher signal than the rest of the brain, locating the basal ganglia in each side is generally not a very difficult task. Choosing the point of maximum intensity as the starting point for 6.1 3-D Morphon segmentation 39 further segmentation is often good enough, however, to increase the robustness of the algorithm, the brain is first multiplied with a weight function, which makes intensity levels closer to the centre of the brain (where the basal ganglia are located) more important. After this, the point of maximum intensity is selected as the initiation point for the 3-D segmentation of each basal ganglia. 6.1.2 Segmentation With a point inside the basal ganglia, the model for the 3-D Morphon segmentation can be initiated. The model here is simply a healthy basal ganglia, which is mirrored when used in the other side of the brain. As explained in section 2.3.2, the basal ganglia are degenerated from the same place if a patient suffers from Parkinson’s disease. This fact can be used as an advantage in the segmentation process. If it is assumed that the relatively unaffected part of the basal ganglia is still high in image signal, the corresponding part of the model can be initiated at the highest intensity point in the image. This is illustrated in 2-D in Figure 6.3, while it is in practice performed in three dimensions. a b Degenerated basal ganglia Model Figure 6.3: a) The model (white) and a degenerated basal ganglia (gray) with the fixed initiation point of the model (square) and the maximum intensity point of the image (circle). b) The model and image after the initiation point of the model has been initiated at the maximum intensity point in the image. With the model initiated at a spot relatively close to the object that is to be segmented, the 3-D Morphon segmentation process can be performed. As with the case of the segmentation of chapter 5, 5.3, the registration process is performed sequentially in multiple resolutions to help the model to fit on a more global scale at first. One question that one might ask is that if the basal ganglia have degenerated, how can the model fit to something that is not there anymore? As a matter of fact, degenerated basal ganglia 40 Chapter 6. Dopamine Transporter Quantification tend to leave a trace, where there used to be dopamine transmitters before degeneration (see Figure 6.4). Since the Morphon is phase based, this trace is as good a structure to fit to as a healthy basal ganglia. Moreover, the model transformation is made relatively rigid to keep the model from deforming too freely in cases where little or none signal is left in some parts of the basal ganglia. Figure 6.4: The faint signal (red) that is left where the basal ganglia has degenerated still works as a structure to register on. After the registration process has completed, the model is thresholded to a small extent in order to remove possible noise or interpolation artifacts, introduced during the registration. The model has now very likely been deformed into a shape that fits well into the area of the brain where the basal ganglia are situated, even if the dopamine transporters have been degenerated. The result of two segmentation processes is presented in Figure 6.5, where the slice of maximum signal intensity of the images has been selected for displaying reasons. 6.2 Quantification After the area of interest, containing whole or parts of basal ganglia, has been successfully segmented the process of quantifying the segmented data remains. This has traditionally been done by medical staff, as described in section 2.3.2, from two-dimensional slices of 3-D volumetric scintigraphic images. However, the method used here will rely on the whole three-dimensional data that has been acquired from the segmentation process. Nonetheless, it will be influenced by the traditional methods in order to be able to compare the results with previous examinations. Quantification is presently performed by selecting multiple regions inside the ROI (the basal ganglia). These regions are then compared by calculating quotes of various kinds. This method has been compared to a manual segmentation method where the region of the basal ganglia has been divided into two parts; one front and one rear part, as can be seen from the contour in Figure 6.5. 6.2 Quantification 41 Figure 6.5: Two examples after the 3-D segmentation process. For displaying reasons, the segmented area is illustrated by a contour on 2-D slices of the 3-D volumetric images. Additionally, the segmented areas have been divided into two parts by a dividing line, in order to extract corresponding parameters. Consequently, the need for finding the long axis of the basal ganglia was needed. In order to achieve this, tools from the statistical domain were used. 6.2.1 Weighted principal component analysis Principal component analysis (PCA) can effectively be used in a dataset to find the direction where the data is varying the most. PCA can be derived in many different ways, depending on the context, however, one property of PCA is that it finds high variance in data. This suits the problem at hand well, as the direction of high variance of voxels is very likely the main axis of the basal ganglia. As maximum variance is desired, finding the local maxima of the variance can be used to derive PCA. If the empirical mean of the dataset is assumed to be zero (without loss of generality), the variance in direction ŵ can be expressed as 2 σŵ = E[xT ŵ] = E[(ŵT x)(xT ŵ)] = ŵT E[xxT ]ŵ = ŵT Cŵ = wT Cw , wT w (6.1) where E denotes the expectation value operator, x a data vector and C the co-variance matrix of x. By differentiating the variance we get 2 ∂σŵ 2 = K(Cw − σŵ w) = 0, ∂w (6.2) 42 Chapter 6. Dopamine Transporter Quantification where K '= 0. Moving around some of the terms and disposing K yields 2 Cw = σŵ w, (6.3) which is identified as an eigenvalue equation: Ce = λe. (6.4) The eigenvectors will, consequently, indicate the direction of highest variance, next highest variance and lowest variance respectively, with all vectors being orthogonal. However, in its original version, PCA on images works with the positions of the pixels (or voxels) in the image only. As low intensity noise will then be as important as the high intensity parts in the centre of the basal ganglia, the direction of variance will much likely not correspond to the long axis of the basal ganglia. To make the procedure more robust, the co-ordinates of the data (voxels) in the image are first weighted with the intensity level at the corresponding position. This can be expressed mathematically if x is the data vector with observations (pixels or voxels) ordered as columns, and the rows representing the different variables (in this case, the co-ordinates (x, y) or (x, y, z)). The weighted data, xw , for row, k, is then expressed as x(k)w = x(k)W, ∀k (6.5) where W is a diagonal weight matrix with the intensity values of the image in the diagonal. The result of this method is illustrated in Figure 6.6. Figure 6.6: Principal component analysis (left) compared to intensity weighted principal component analysis (right) with test data where a brighter color indicates higher intensity values. The solid line illustrates the eigenvector with the corresponding highest eigenvalue, i.e. the direction of highest variance or highest weighted variance. This will give the means to approximate the long axis of the basal ganglia in order to find the front and back of the organ, as illustrated by the dividing line in Figure 6.5. The front and back part of the basal ganglia is here defined as dividing the ganglia at a certain point along the long axis. If the segmentation was successful, this would approximate dividing the ganglia with a plane, having the long axis vector as the normal vector. 6.3 Summary 6.3 43 Summary The quantification of DaTSCAN-images can be performed through first dividing the brain into two halves. Each part will then be target for a single 3-D Morphon segmentation, which leads to the localisation of the basal ganglia. By finding the long axis of the two ganglia, they can then be divided into parts, and several fractions and values can be extracted. 7 Results In this chapter, the results from the automatic segmentation and alignment of the myocardial perfusion images and the quantification of DaTSCAN SPECT-images will be presented in two separate parts. Regarding the current implementation of the methods, it can be noted that they both take around 15 seconds per image to perform their respective task. 7.1 Segmentation and alignment of 3-D transaxial myocardial perfusion images The segmentation and alignment algorithm can be divided and tested in two parts; the segmentation of the left ventricle, and the angling of the left ventricle after segmentation. The segmentation is obviously a necessary step for the alignment to work properly, but can nonetheless be interesting as a separate segmentation method. 7.1.1 Segmentation In order to test the success of the segmentation algorithm implemented in this thesis, a large number of randomly selected myocardial perfusion images has been used. The original images have all been acquired immediately after image reconstruction in the γcamera workstation; often called transversal or transaxial images. No attention has been paid to different reconstruction algorithms, as they are estimated to have little effect on the final result. The material consists of images from both male and female patients, varying in age. Moreover, as only patients showing symptoms of a heart disease are examined at the hospital where the images have been acquired, the images are not representative to the perfusion of an average person, but often indicates some kind of heart disorder. 46 Chapter 7. Results 100 images have been used to test the algorithm. Since automatic evaluation can be difficult for segmentation algorithms, all the images have been visually evaluated after the segmentation. The importance of the segmentation in this context is to crop the large transversal image volumes into a small image volume containing essentially only the left ventricle. No effort has been made to remove noise and/or other organs that may be situated close to the heart, as they can be of help to medical staff when examining the images. The segmentation was evaluated to have been completely successful in 100 of the 100 cases, that is in 100 percent. Some examples from the 100 tested images can be seen in figure Figure 7.1. Another factor that may be of interest when evaluating the segmentation process is how well the 3-D model deformed into the target image. Examples of this are shown in Figure 7.2, where the deformed model, corresponding to the images in Figure 7.1, are displayed. Note that the above images have not yet been rotated, but only target for segmentation. 7.1.2 Alignment After the 100 images above had been segmented, some of these were rotated with corresponding estimated angles. Two angles was used to rotate the heart and thus the rotation around the axis of the heart was neglected as it has lower priority compared to the main, global, rotation. Manual rotation of the same images was also performed by a technologist on 60 of the 100 images. These manual operations were made in the ordinary clinical environment that is used when manually adjusting the images after image reconstruction. The manual alignment was therefore carried out completely independently of the algorithm. Angles estimated from an application at the workstation were also included to give further data to compare to. This software, however, works on already manually segmented images. The estimated angles for each of the involved parts (the algorithm used in this thesis, the manual estimation and the additional semi-automatic estimation) are presented in Figure 7.3 and 7.4. The mean difference for the automatic method was approximately 6 and 7 degrees for the two estimated angles. However, there were peaks of differences of up to 30 degrees. Additionally, in Figure 7.5 there are some examples of more and less successful rotations made by the automatic algorithm, displayed in the same way as above. 7.2 Automatic dopamine transporter quantification As there are few developed commercial applications performing automatic 3-D quantification of DaTSCAN-images, the results of this part of the thesis consist much in considering the correlation between the automatic method introduced here with manual 7.2 Automatic dopamine transporter quantification 47 Figure 7.1: Results from the automatic segmentation displayed as appropriate slices along all three axes in each image. Note the great variation between the different hearts. 48 Chapter 7. Results Figure 7.2: The deformed models corresponding to the images in Figure 7.1, displayed in the same slices. 7.2 Automatic dopamine transporter quantification 49 *! )! (! '! &! %! $! #! "! !+ ! "! #! $! %! &! ,-./01.23 415-16 ,-./!015+72889:9539 ;902!1-./01.23 ;902!1-./!015+72889:9539 + '! Figure 7.3: The first of the two angles in degrees, named HLA, estimated with different methods. The dotted and dashed horisontal lines indicate the mean difference for the automatic and semi-automatic methods respectively. 50 Chapter 7. Results "!! *! )! (! '! &! %! $! #! "! !+ ! "! #! $! %! &! ,-./01.23 415-16 ,-./!015+72889:9539 ;902!1-./01.23 ;902!1-./!015+72889:9539 + '! Figure 7.4: The second of the two angles in degrees, named VLA, estimated with different methods. The dotted and dashed horisontal lines indicate the mean difference for the automatic and semi-automatic methods respectively. 7.2 Automatic dopamine transporter quantification Figure 7.5: Slices through volumes after rotation has been performed. 51 52 Chapter 7. Results 2-D quantification methods. As in the previous section, the results from the automatic quantification can be divided into a segmentation part and a quantification part. The material that the method was tested on was made up of 70 images, taken directly after image reconstruction in the γ-camera. 7.2.1 Segmentation The segmentation process was here, as in the previous results, evaluated manually for each image and failed in one case of the 70 images. This was due to the fact that the uptake in the basal ganglia of one side of the examined brain was lower than in other parts of the brain, resulting in that the model of the segmentation process was initiated too far from the basal ganglia. The segmentation did, however, succeed for the other side of the brain. This gives a rate of success of approximately 99 percent. Images of successful segmentations are presented in Figure 7.6. Figure 7.6: Illustrating the results from the segmentation process, where the contour line around the basal ganglia indicates the segmented area. 7.2.2 Quantification As have been mentioned, there are, at the time of writing, few algorithms that perform automatic 3-D quantification of DaTSCAN-images, and the quality of the result can 7.2 Automatic dopamine transporter quantification 53 therefore be difficult to define. Nevertheless, even though the technique presented here operates in three dimensions, it should, if performing well, correlate with manual two dimensional approaches. Automatic quantification has therefore been performed on the same images as the segmentation process, and a set of different values have been calculated, which are often used in clinical quantification of this kind of images. The quantification values are defined by different fractions between whole or parts of the basal ganglia signal and the background signal in the brain, as well as fractions between the left and right basal ganglia, and the front and back parts (as defined in the last paragraph of section 6.2.1) of each ganglia. These values are explained and clarified further in Figure 7.7. With these areas, a number of different fractions, fi , can be defined A1 A2 B1 C B2 Figure 7.7: The different fractions between different parts of the basal ganglia and the background signal are defined by the areas above. as f1 = f5 = A1 +A2 −C 2 −C , f2 = B1 +B , C C f1 A2 B2 , f6 = B1 , f7 = f2 , A1 f3 = A2C−C , f8 = ff34 f4 = B2 −C C (7.1) where C is the mean signal of the whole brain, excluding the basal ganglia. The different fractions are illustrated in Figure 7.8, 7.9, 7.10 and 7.11. 54 Chapter 7. Results 5 5 4 4 3 3 2 2 1 1 10 20 30 40 50 10 Correlation:0.89803 20 30 40 50 Correlation:0.91175 4 4 3 3 2 2 1 1 1 2 3 4 5 1 2 3 4 5 Figure 7.8: The fractions f1 and f2 with the values of manual (green) and automatic (blue) quantification as well as the relative difference (red) along with scatter plots for both sides. 7.2 Automatic dopamine transporter quantification 5 5 4 4 3 3 2 2 1 1 10 20 30 40 50 55 10 Correlation:0.91397 20 30 40 50 Correlation:0.9189 4 4 3 3 2 2 1 1 1 2 3 4 5 1 2 3 4 5 Figure 7.9: The fractions f3 and f4 with the values of manual (green) and automatic (blue) quantification as well as the relative difference (red) along with scatter plots for both sides. 56 Chapter 7. Results 1.2 1 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 10 20 30 40 50 10 Correlation:0.79792 20 30 40 50 Correlation:0.84629 1.1 1 1 0.9 0.9 0.8 0.8 0.7 0.6 0.7 0.5 0.6 0.8 1 1.2 0.6 0.8 1 1.2 Figure 7.10: The fractions f5 and f6 with the values of manual (green) and automatic (blue) quantification as well as the relative difference (red) along with scatter plots for both sides. The manual values available were rounded to one digit, which explains the discretization of the horizontal axis. 7.2 Automatic dopamine transporter quantification 57 %!!&!! %!! &! &! &!! ! ! !&!! !&! ! !&!! !&! !%!! !"!! !%!! !"!! ! !%&! ! "! #! $! !%!! !%&! ! ! "! "! #! #! $! $! !%!! ()**+,-./)01!2345"5 '())*+,-.(/0!12&222 '())*+,-.(/0!12&222 &! '! '! ! ! ! ! !&! !&!!'! !'! !%!! !%!! !&!! !&!! !&! ! &! !%!! !%!! !&! !"!! ! !&!! "! # ()**+,-./)01!2345 &! !%!! ! !&! Figure 7.11: The fractions f7 and f8 with the values of manual (green) and automatic (blue) quantification as well as the relative difference (red) along with scatter plots for both sides. !%!! !"!! !&!! 8 Discussion In this chapter, some general comments will be made to the results in chapter 7. Furthermore, possible future improvements to the presented methods that, due to the time limit of this project, were not implemented, will be proposed. 8.1 Segmentation and alignment of 3-D transaxial myocardial perfusion images From the results it is quite obvious that the automatic segmentation scheme presented in this thesis is near to flawless when applied to myocardial perfusion SPECT-images. The relatively large dataset along with the great variation among these kind of medical images, gives great credibility to this local phase based registration scheme for segmenting the left ventricle of the heart. The initial 2-D segmentation is probably essential in that it removes other organs that can resemble the left ventricle to quite some extent from time to time. Additionally, the 3-D segmentation fine-tunes the model to the target image, and if desired, an even tighter cropping could probably be performed than the one illustrated in Figure 7.1. As noted though, the surrounding organs of the left ventricle can be helpful for medical staff when diagnosing the images. Performing the registration with different models have not been performed to any substantial extent in this thesis. However, from the results it is obvious that the choice of model can not be crucial when it comes to segmentation; backed up by the great variance among different hearts. However, in some cases, where the target heart has been overly large, the 2-D segmentation can cut away some parts of the heart due to restraints in rigidity. While this does not generally have any impact on the final result after the 3-D segmentation has been performed, it does increase the possibility of a bad angle estimation. The results from the alignment can, compared to that of the segmentation, be directly 60 Chapter 8. Discussion compared to other data, such as the manual angle estimations. As the angling is a more complex process, the automatically estimated angles do vary some with the manual measurement and as could be seen, the semi-automatic method have a lower mean difference than the fully automatic method used in this thesis. It should be noted though, that the difference between the manual and the semi-automatic methods sometimes reaches a value of zero. This can be explained due to the fact that the semi-automatic method is built in to the workstation where the operator performs the manual estimations. The operator is first presented with angles from the semi-automatic application, and could possibly deem the presented angles as sufficient; therefore not changing them further manually. Moreover, as the deformation of the model to the target images seems very well performed, the flaw of the angle estimation might be founded in the way that the difference in angles is described and defined. Not uncommonly, the left ventricle of the examined image is somewhat curved, in which case a line description for describing the orientation of the object could be insufficient. Tests with two lines as describing the angle difference has been performed, but without any obvious improvement. Since the deformation field of the 3-D registration is known and probably a good description of some kind of difference between the model and target image, future implementations of angle estimation can be easily done. Moreover, performing the registration with a different kind of model might prove itself useful when it comes to the angle estimation since the difference between the target image and the model could correlate better with the difference in angle for another model. Furthermore, the absolute angle of the left ventricle may not be important in an absolute, single estimation, but is probably more important when comparing different images from the same patient. One solution to this could then be to register the left ventricle in one examination to the same ventricle in another examination. Since the two images will probably be more alike compared to a general model, the angle difference estimation between the hearts of the different examinations could be easier determined. It is, however, difficult to determine how much the rotation of a single heart can vary from a "perfect" rotation and still be sufficient for a doctor to base a diagnose on. Generally though, a difference of more than 10 degrees often results in a poor rotated image. Furthermore, a perfect rotation is hard to define, as different operators will rotate the same heart differently. Therefore, to gain a full understanding on how successful the algorithm of this thesis is in rotating the images, a study involving more human operators is desirable. It is also difficult to compare this method to already proposed methods, since information about image type and quality is not available in enough detail for such studies. 8.2 Automatic dopamine transporter quantification 8.2 61 Automatic dopamine transporter quantification The automatic quantification of DaTSCAN-images showed itself to be quite successful when it comes to correlation to manual 2-D quantification. There is very high correlation in some cases of the different fractions, however, a relevant question to ask is if the correlation should be higher. Probably not, since the two methods differ very much. The automatic method uses volume quantification, while the manual quantification is performed on a number, or sometimes only one, two dimensional slices of the volume. The segmentation process was successful in most cases, and could probably be even more so if a more sophisticated method for initiating the registration model was developed. A pre-registration of the whole brain could primarily be performed, which would give a better estimation of where the basal ganglia should, or more important should not, be located. For very low uptake, the registration model could sometimes float away, in lack of structure to register on. This behaviour could be removed to some extent if one of the two basal ganglia have a higher uptake. By first registering on the side with high uptake, a rough approximation of the other basal ganglia could be generated. By then increasing the regularisation kernel (increasing the rigidity of the model), and mirroring the result from the first registration, the registration of the basal ganglia with low uptake could probably be helped; taking into account that the two basal ganglia of the same brain do not differ much from each other. Coinciding with suggestions of the earlier section, other registration models should be evaluated to investigate if that could yield a better result. However, as the uptake of the basal ganglia is due to a physiological process, this is unlikely. If CT and/or MRI images of the same brain are available, the registration could be performed on these images (with much higher resolution) and later mapped onto the SPECT-images of the dopamine activity in the basal ganglia. 9 Conclusions In this thesis, it has been showed that a phase based registration scheme can be very successful when performing fully automatic segmentation of myocardial perfusion SPECTimages. Such a method has been implemented and when performed in three dimensions, this segmentation can be used to estimate the angle of the left ventricle. To reduce variability between different operators, such a method can further more be used to take one step closer to a fully automatic examination of myocardial perfusion images. Additionally, a method for automatically quantifying DaTSCAN-images in three dimensions was presented with promising results. Manual quantification can be difficult and tedious and is often performed on slices instead of whole volume data. This method can therefore increase the quality of examinations and vastly decrease the time that it takes to quantify each image. As the research on automatic algorithms for dopamine transporter quantification is currently quite sparse, the hope that this method will give medical staff future tools for increasing examination quality is likely well founded. Bibliography [1] G. Germano, P.B. Kavanagh, Hsiao-Te Su, M. Mazzanti, H. Kiat, R. Hachamovitch, K.F. Van Train, J.S. Areeda, and D.S. Berman. Automatic reorientation of three-dimensional, transaxial myocardial perfusion spect images. The Journal of Nuclear Medicine, 1995. [2] G. Germano, P.B. Kavanagh, J. Chen, P. Waechter, Hsiao-Te Su, H. Kiat, and D.S. Berman. Operator-less processing of myocardial perfusion spect studies. The Journal of Nuclear Medicine, 1995. [3] R.J. Morton, M.J. Guy, R. Clauss, P.J. Hinton, C.A. Marshall, and E.A. Clarke. Comparison of different methods of datscan quantification. Nuclear medicine communications, pages 1139–1146, 2005. [4] P.A. Tipler and R.A. Llewellyn. Modern Physics. W. H. Freeman and Company, New York, USA, fourth edition, 2004. [5] A.C Perkins. Nuclear Medicine in Pharmaceutical Research, chapter 2. CRC Press, London, UK, fourth edition, 1999. URL http: //site.ebrary.com.lt.ltag.bibl.liu.se/lib/linkoping/ Doc?id=10054842&ppg=5. [6] A. Del Guerra. Ionizing Radiation Detectors for Medical Imaging. World Scientific Publishing Company, Incorporated, Singapore, third edition, 2004. URL http://site.ebrary.com.lt.ltag.bibl.liu.se/ lib/linkoping/Doc?id=10082183&ppg=5. [7] O. Chiewitz and G. de Heversy. Radioactive indicators in the study of phosphorus metabolism in rats. Nature, 1935. [8] E. Lindgren. Versuche mit radioaktiven isotopen bei leukämibehandlung. Acta Radiologica, 1944. [9] H.W. Strauss, K. Harrison, and J.K. Langee. Thallium-201 for myocardial imaging. relation of thallium-201 to regional myocardial perfusion. Circulation, 1975. [10] B. Bodforss. Radioisotope scanning of the brain. (32), 1965. [11] P.V. Harper, G. Andros, and K. Lathrop. Technetium-99 as a biological tracer. The Journal of Nuclear Medicine, 1962. 66 Chapter 9. Conclusions [12] S.A. Larsson. Gamma camera emission tomography. development and properties of a multi-sectional emission computed tomography system. 1980, Acta Radiologica. [13] C.G. Wilson, Y.P. Zhu, and M. Frier. Nuclear Medicine in Pharmaceutical Research, chapter 8. CRC Press, London, UK, fourth edition, 1999. URL http://site.ebrary.com.lt.ltag.bibl.liu.se/ lib/linkoping/Doc?id=10054842&ppg=5. [14] GE Healthcare. Datscan.com, January 2008. URL http://www.datscan. com. [15] H.W. Strauss and D.D. Miller. Society of Nuclear Medicine Procedure Guideline for Myocardial Perfusion Imaging. Society of Nuclear Medicine, 3.0 edition, June 2002. [16] K. Tatsch, S. Asenbaum, P. Bartenstein, A. Catafau, C. Halldin, L.S. Pilowsky, and A. Pupi. European Association of Nuclear Medicine Procedure Guidelines For Brain Neurotransmission SPET using 123 I-labelled Dopamine Transporter Ligands. European Association of Nuclear Medicine, October 2001. [17] G.H. Granlund and H. Knutsson. Signal Processing for Computer Vision. Kluwer Academic Publishers, 1995. ISBN 0-7923-9530-1. [18] B. Svensson, J. Pettersson, and H. Knutsson. Bildregistrering: Geometrisk anpassning av bilder, May 2007. URL http://www.imt.liu.se/edu/ courses/TBMI45/pdfs/registration.pdf. [19] H. Knutsson and M. Andersson. Morphons: Paint on priors and elastic canvas for segmentation and registration. In Proceedings of the Scandinavian Conference on Image Analysis (SCIA), Joensuu, June 2005. [20] J. Pettersson. Automatic generation of patient specific models for hip surgery simulation. Lic. Thesis LiU-Tek-Lic-2006:24, Linköping University, Sweden, April 2006. Thesis No. 1243, ISBN 91-85523-95-X. [21] B. Rodrìguez-Vila, J. Pettersson, M. Borga, F. Garcìa-Vicente, E.J. Gómez, and H. Knutsson. 3d deformable registration for monitoring radiotherapy treatment in prostate cancer. In Proceedings of the 15th Scandinavian conference on image analysis (SCIA’07), Aalborg, Denmark, June 2007. [22] J. Pettersson, K.L. Palmerius, H. Knutsson, O. Wahlström, B. Tillander, and M. Borga. Simulation of patient specific cervical hip fracture surgery with a volume haptic interface. IEEE Transactions on Biomedical Engineering, 2007. 67 [23] A. Parraga, A. Susin, J. Pettersson, B. Macq, and M. De Craene. Quality assessment of non-rigid registration methods for atlas-based segmentation in headneck radiotherapy. In Proceedings of IEEE International Conference on Acoustics, Speech, & Signal Processing, Honolulu, Hawaii, USA, April 2007. [24] H. Knutsson, C-F. Westin, and G.H. Granlund. Local multiscale frequency and bandwidth estimation. In Proceedings of the IEEE International Conference on Image Processing, pages 36–40, Austin, Texas, November 1994. IEEE. (Cited in Science: Vol. 269, 29 Sept. 1995). [25] H. Knutsson, M. Andersson, and J. Wiklund. Advanced filter design. In Proceedings of the 11th Scandinavian Conference on Image Analysis, Greenland, June 1999. SCIA. [26] M. Andersson and H. Knutsson. Controllable 3-D filters for low level computer vision. In Proceedings of the 8th Scandinavian Conference on Image Analysis, Tromsø, May 1993. SCIA. URL http://www.imt.liu.se/mi/ Publications/Papers/scia93_ak.pdf. [27] H. Knutsson and C-F. Westin. Normalized convolution: A technique for filtering incomplete and uncertain data. In Proceedings of the 8th Scandinavian Conference on Image Analysis, Tromsö, Norway, May 1993. SCIA, NOBIM, Norwegian Society for Image Processing and Pattern Recognition. Report LiTH–ISY–I–1528. Linköpings tekniska högskola Institutionen för medicinsk teknik Rapportnr: LiTH-IMT/MI30-AEX--08/465--SE Datum: 2008-04-04 Svensk titel Segmentering och uppvinkling av tredimensionella, transaxiella myokardiska perfusionsbilder och automatisk dopaminreceptorkvantifiering Engelsk titel Segmentation and Alignment of 3-D Transaxial Myocardial Perfusion Images and Automatic Dopamin Transporter Quantification Författare Leo Bergnéhr Uppdragsgivare: EXINI Diagnostics Rapporttyp: Examensarbete Rapportspråk: Engelska Sammanfattning Abstract In this thesis, a novel method for automatically segmenting the left ventricle of the heart in SPECT-images is presented. The segmentation is based on an intensity-invariant localphase based approach, thus removing the difficulty of the commonly varying intensity in myocardial perfusion images. Additionally, the method is used to estimate the angle of the left ventricle of the heart. Furthermore, the method is slightly adjusted, and a new approach on automatically quantifying dopamine transporters in the basal ganglia using the DaTSCAN™ radiotracer is proposed. The results for both applications are promising. The segmentation for myocardial perfusion images succeeded in 100 of 100 cases with a mean difference to manually estimated angles of around 8 degrees. The automatic quantification algorithm showed good correlation with manual quantification, with a correlation coefficient of up to 0.95 for 70 images. Nyckelord Keyword Segmentation, Morphon, SPECT, Myocardial, DAT Bibliotekets anteckningar: