Download Document 8935429

(1) Radical Equations.notebook
Solving Radical Equations
A "radical" equation is an equation in which the variable is hiding inside
a radical symbol (in the radicand). is a radical equation
is NOT a radical equation
To solve radical equations:
1. Isolate the radical (or one of the radicals) to one side of the equal sign.
2. If the radical is a square root, square each side of the
equation. (If the radical is not a square root, raise each side to a power
equal to the index of the root.)
3. Solve the resulting equation.
4. Check your answer(s) to avoid extraneous roots.
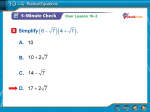
Examples: 1.
square both sides
(
(2
x ­ 1 = 4
x = 5
{5}
2
(1) Radical Equations.notebook
Check:
2.
√2x ­ 1 = ­3
2x ­ 1 = 9
2x = 10
x = 5
isolate radical
√2(5) ­ 1 + 5 = 2
√10 ­ 1 + 5 = 2 √9 + 5 = 2
3+5=2
8=2 X
x = 5
extraneous
3. 5√2x + 3 -5 = 40
Check:
5√2x + 3 = 45 add 5
√2x + 3 = 9 divide by 5
2x + 3 = 81square both sides
2x = 78
x = 39
{39}
4.
(
(
2
(
(
5√2(39) + 3 - 5 = 40
5√78 + 3 - 5 = 40
5√81 - 5 = 40
5(9) - 5 = 40
45 - 5 = 40
40 = 40
2
square both sides
x2 ­ 2x + 1 = 5x ­ 9
x2 ­ 7x + 10 = 0
(x ­ 5)(x ­ 2) = 0
x = 5 x = 2
REMEMBER:
A binomial squared: FOIL
Quadratic: set = 0 and factor
Check:
5 ­ 1 = √5(5) - 9
4 = √25 - 9
4 = √16
4=4
{2,5}
2 ­ 1 = √5(2) - 9
1 = √10 - 9
1 = √1
1=1
(1) Radical Equations.notebook
5.
5x + 3 = 3x + 7
2x + 3 = 7
2x = 4
x = 2
radical on both sides:
square both sides
Check:
{2}
√5(2) + 3 = √3(2) +7
√10 + 3 = √6 + 7
√13 = √13
6.
Solve and check:
the radical has a coefficient
square the coefficient when
squaring both sides
{2,6}
(1) Radical Equations.notebook
7.
2 ∛x + 9 = 3
(∛x
2 (
3
3
+ 9 = 3
since this equation has a cube root,
raise each side the the third power
x2 + 9 = 27
x2 = 18
x = ±√18
x = √9 √2
x = ±3√2
A check should be done!!