Download 

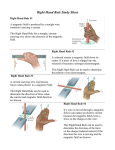
Physics 2020
Spring 2009
Stephan LeBohec
DATA SHEET - EXAM 4
SEAT #
Constants & mathematics:
1
9
2
−2
k=
=8.99×10 N⋅m ⋅C
4  0
0=4 ×10−7 T⋅m⋅A−1
cos 2  f t 
≈−2  f sin 2  f t 
t
Magnetic force and field:
 ∣=∣q∣⋅∣v∣⋅∣ 
Magnetic force on a charge: ∣F
B∣sin 
Magnetic field produced by an infinitely long wire:
 I
∣
B r ∣= 0
2 r
Electromagnetic induction:
Magnetic flux: = A⋅∣
B∣cos 
Mutual inductance: M =
Self inductance: L=
Transformers:
S
IP

I
VS NS IP
=
=
V P NP IS
−19
e=1.602×10 C
Q Proton =e & Q Electron=−e
c=
1
=299,792,458 m⋅s−1≈3×10 8 m⋅s−1
 0 0
sin 2 f t 
≈2  f cos 2  f t 
t
 ∣=I⋅L∣ 
Magnetic force on a current: ∣F
B∣sin 
Magnetic field inside a solenoid:
∣
B∣=0 n I
Faraday's law: V =−

t
Mutual induction: V =−M
Self induction: V =−L
I
t
I
t
Work, force & displacement relation
 ∣⋅ x⋅cos 
 W =∣F
Electromagnetic waves:
=c⋅T =c / f
Doppler effect: f o= f s
1±v o /c
≈ f s 1±v rel /c 
1∓v s /c
Reflection of light:
Law of reflection: R =I
Mirrors equation:
1 1
1
= 
f dI dO
Malus law: I T =I I cos 2 
Spherical mirror: f =
Magnification: M =
R
2
hO
d
=− I
hI
dO
Physics 2020
Spring 2009
Stephan LeBohec
Name:_____________________________________
TA (circle one): Adam
A)
1
EXAM 4
Isaac
Michael
Student ID #:___________________________
Sarah
[36 points, 3 points per question] For each statement, circle all the options you find appropriate.
You do not need to show your work.
1) A straight current carrying wire is placed in a uniform magnetic field. The magnetic field does not cause the
wire to move. What is the angle between the magnetic field and the direction of the current in the wire?
0°
45°
90°
2) A charged particle has a velocity making an
RECTILINEAR
CIRCULAR
80
°
angle with a uniform magnetic field. The trajectory is
HELICOIDAL
3) At time t =0 , an electron has a speed v parallel to a wire transporting a current in the same direction as
the velocity of the electron. The magnetic force acting on the electron is directed
TOWARD THE WIRE
ALONG THE WIRE
AWAY FROM THE WIRE
4) A conductive solid rod moves through a uniform magnetic field. Taking into account electromagnetic effects,
the rod
SLOWS DOWN
HAS A CONSTANT SPEED
ACCELERATES
5) Two frictionless rails on an incline are connected by a resistor. A uniform magnetic field is pointing upward.
A conductive rod in contact with both rails is free to slide along the rails. After a long time, the rod
STOPS
HAS A CONSTANT SPEED
KEEPS ACCELERATING
6) A conductive ring is inside a solenoid. When a clockwise current is turned on in the solenoid, the induced
current in the ring is
CLOCK WISE
ZERO
COUNTER CLOCK WISE
°
7) Unpolarized light is sent through two polarizers that are aligned with 90 between their transmission axes.
At which angle should the transmission axis of a third polarizer be when it is placed between the two
polarizers so that some light leaves the system of polarizers.
0°
45°
90°
180°
8) In a glass maze, I see the wrist watch of my friend going clockwise. The number of mirrors through which I see
her/his image is
EVEN
ODD
ZERO
9) A concave mirror can only produces real images.
TRUE
FALSE
10) A convex mirror can only produces virtual images.
TRUE
FALSE
11) Light emitted at the center of curvature of a concave mirror is reflected back to
THE FOCUS
THE CENTER OFCURVATURE
INFINITY
12) A laser beam arrives on a flat mirror. In order to change the direction of the reflected beam by an angle
the mirror must be rotated by
/2

2
 ,
Physics 2020
Spring 2009
Stephan LeBohec
Name:_____________________________________
TA (circle one): Michael
B)
2
EXAM 4
Sarah
Adam
Student ID #:___________________________
Isaac
A straight copper wire of cross section area A=9.0×10−8 m 2
and length L=20cm carries a current I 1=9.0A . It is
horizontal and levitating above an infinitely long wire also carrying
a current I 2=18A as shown on the figure. (copper density
=9,000 kg⋅m−3 and g=10 m⋅s−2 ).
KB
1) [4 points] On the figure, clearly indicate the direction of the
current in the top wire.
Using the second right hand rule first to figure the direction of the magnetic field and then using the first right hand rule
to figure the direction of the force, one finds the current must flow to the left.
2) [12 points] What is the distance between the two wires?
The magnetic force has to be put in equation with the gravitational force
F =I 1⋅L⋅B= A⋅L⋅⋅g with the magnetic
0⋅L⋅I 1⋅I 2
 ⋅I ⋅I
0 I 2
= 0 1 2 and, numerically, we have
field B=
so, solving for h , we get: h=
2 A⋅L⋅⋅g 2 A⋅⋅g
2 h
−7
−1
4 ×10 T⋅m⋅A ×9 A×18 A
h=
=4×10−3 m=4 mm
−8 −2
3
−3
−2
2×9×10 m ×9×10 kg⋅m ×10 m⋅s
C)
A 2cm tall object is placed
curvature.
1.0m away from a concave spherical mirror with a 0.40m radius of
1) [3 points] Is the image formed real or virtual?
The object is at a large distance from the mirror larger than the focal length (half of curvature radius) so the image is
real.
2) [3 points] Is the image formed inverted or not?
The image is inverted.
3) [8 points] What is the height of the image?
R
=0.2 m and the distance of the object is d o=1 m . Using the mirror equation,
2
1 1 −1
1 1 −1
d i= −  =
−  =0.25 m . Then with h o=2 cm , the image is
f do
0.2 1
di
0.25 m
hi =h o =2 cm×
=0.5 cm tall.
do
1.0 m
The focal length is f =
Physics 2020
Spring 2009
Stephan LeBohec
Name:_____________________________________
TA (circle one): Michael
D
3
EXAM 4
Sarah
Adam
Student ID #:___________________________
Isaac
A rectangular circuit with a resistance R=20  , a width a=0.10 m
and a height b=0.20 m moves at a constant speed ∣v∣=10 m⋅s −1 from
region 1 with a magnetic field B1 to region 2 with a magnetic field B2 as
indicated on the figure ( ∣B1∣=∣B2∣=0.5 T ).
I
1) [4 points] On the figure, clearly indicate the direction of the current
induced in the circuit as the circuit is entering region 2.
Using Lenz's law and the second right hand rule, one finds the current flows counterclock-wise.
2) [8 points] Calculate the current in the circuit while it is entering region 2.

V 1  1 
= ∣ B1∣∣B2∣ b⋅∣
v∣ .
and the current is I = =
R R t R
t
Numerically I =0.5T0.5T×0.2m ×10 m⋅s−1 /20 =0.1 A .
The induced electromotive force is V =−
3) [8 points] What is the total amount of energy dissipated in the resistor while it was entering region 2?
The power dissipated is P=R⋅I 2 and it goes on for a duration  t =a /∣v∣ so the total energy dissipated in the
resistor is  W R= R⋅I 2⋅a /∣v∣=20 ×0.1 A2×0.1 m/10 m⋅s−1=2×10−3 J =2mJ
4) [7 points] What is the magnitude of the force the operator must apply to maintain the constant speed of the
circuit while it is entering region 2?
The total magnetic for on the circuit has a magnitude
F =0.1A×0.2 m×0.5T 0.5 T =0.02 N
F =I⋅b⋅∣B1∣I⋅b⋅∣B2∣=I⋅b ∣B1∣∣B2∣ , so , numerically,
5) [7 points] Using your response to the previous question, calculate the total amount of work required by the
operator to bring the circuit inside region 2 at constant speed.
How does it compare with your answer to question 3)? Comment.
The work done by the operator is  W Op= F⋅a=0.02 N ×0.1 m=0.002 J =2 mJ which is equal to the total amount
of energy dissipated in the resistor obtained in question 3). All the work done by the operator is converted in electric
energy dissipated in the resistor.