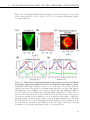
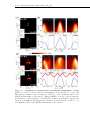
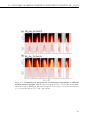
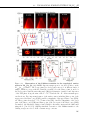
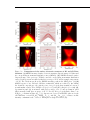
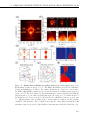
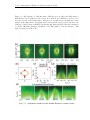
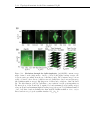
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Discoveries of New Topological STates of Matter Beyond Topological Insulators
Jahn–Teller effect wikipedia , lookup
Superconductivity wikipedia , lookup
Pseudo Jahn–Teller effect wikipedia , lookup
Self-assembled monolayer wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Density of states wikipedia , lookup
High-temperature superconductivity wikipedia , lookup
Geometrical frustration wikipedia , lookup
Dirac equation wikipedia , lookup
Ultrahydrophobicity wikipedia , lookup
Energy applications of nanotechnology wikipedia , lookup
Surface tension wikipedia , lookup
Tunable metamaterial wikipedia , lookup
Sessile drop technique wikipedia , lookup
Semiconductor wikipedia , lookup
Nanochemistry wikipedia , lookup
Discoveries of New Topological States of Matter Beyond Topological Insulators Su-Yang Xu A Dissertation Presented to the Faculty of Princeton University in Candidacy for the Degree of Doctor of Philosophy Recommended for Acceptance by the Department of Physics Advisor: M. Zahid Hasan January 2015 c Copyright by Su-Yang Xu, 2014. All Rights Reserved Abstract The discoveries of new forms of matter have been so definitive that they are used to name periods in the history of mankind, such as Stone Age, Bronze Age, and Iron Age. Although all matter is composed of component particles, particles can organize in various ways leading to different phases of matter. Finding all possible distinct phases that matter can form and understanding the physics behind each of them are fundamentally important goals in physics research and often lead to new technologies, benefiting our society. A topological phase is an unusual type of crystalline solid, characterized by a nontrivial topological number. This number is a global quantity, which depends on the crystal’s bulk electronic wavefunctions. In 2007, the 3D Z2 topological insulator (TI) phase was discovered in bismuth-based materials, marking the first realization of a topological phase in bulk crystals. A 3D TI features spin-polarized Dirac electronic states on its surface, which enjoys a robust protection against disorder. This discovery tremendously accelerated the field and led to a surge of interest in searching for new topological phases of matter. In this thesis, we present the experimental discovery of several new topological phases and phenomena beyond the Z2 TI, including the topological quantum phase transition in BiTl(S1−δ Seδ )2 , the topological crystalline insulator phase in Pb1−x Snx Te(Se), the topological Dirac semimetal phase in Cd3 As2 and Na3 Bi (featuring Fermi arc surface states), evidence for the topological Kondo insulator state in SmB6 , and the demonstration of superconductivity and magnetism in the surface states of the prototypic TI Bi2 Se3 . Each of these new states exhibits topological surface states with unique protected properties. They may be useful in developing future technologies such as fault-tolerant topological quantum computers and low-power spintronic devices, which will revolutionize our electronic and energy industries. The new topological states of matter presented here are currently being studied by many groups worldwide. With our discoveries, the “topological world” has begun to unveil itself. We believe that this is only the tip of the iceberg. Our ongoing work suggests that there are many more with yet more exciting properties awaiting discovery. iv Acknowledgements First and foremost, I would like to thank my advisor Prof. M. Zahid Hasan for his mentorship and support. He has been a constant source of encouragement and advice throughout my graduate studies. I will always remember his words: “The idea is to keep trying. Everyone will face failure. But if we keep trying, on average we will do fine.” Every time I ran into difficulties with my experiments or when fighting in the reviewers to get a paper published, these words encouraged me. Indeed, now I understand that there is no sure path to success, and the key is to “keep trying”. I also tremendously benefited from his ability to understand and explain the essences of physics without bringing many formulations, and his insights into condensed matter physics, especially when it came to looking for the next exciting topics in our field. This is one of the main driving forces to maintaining our group of front line in the fierce competition. Moreover, I am grateful for the freedom he gave me and also every other member in our group to pursue individual interests in our research work. He allowed us to come up with our own research projects, design our own experiments and consult experts in relevant areas such as ARPES technique, material growth and condensed matter theory. I sincerely thank Zahid for every single aspect of my graduate research. I am also indebted to my colleagues and friends in my group. I wish to thank David Hsieh, Dong Qian, and Matthew Xia for introducing me into the group and helping me settle down. Andrew Wray taught me how to use ARPES and was extremely generous as a teacher when I started to work with ARPES on topological insulators. Madhab Neupane, Chang Liu and Nasser Alidoust have been wonderful teammates in experiments, and Madhab and Chang have also been great friends in my personal life. I thank Ilya Belopolski for his infinite curiosity when it came to new physics and for always being unsatisfied with the answers that I provided to his questions. This drove me crazy but lead to many new and exciting ideas. I thank Guang for being vi not only a wonderful labmate, but also such a reliable friend. I thank him for his generous help when I got into trouble. During my Ph.D. studies, I was very lucky to have the unique opportunity to work at ARPES beamlines at synchrotron radiation laboratories all over the world. At these facilities, I learned a lot from many wonderful local scientists and staff. I thank Alexei Fedorov, Sung-kwan Mo, Jonathan Denlinger and Zahid Hussain at the ALS in Berkeley. I thank Makoto Hashimoto and Donghui Lu at the SSRL in Stanford. I thank Hugo Dil, Fabian Meier, Bartosz Slomski, Gabriel Landolt and Vladimir Strocov at the SLS in Switzerland. I thank Mats Leandersson, Thiagarajan Balasubramanian, Johan Adell and Craig Polley at MAX-lab in Sweden. I thank Jaime Sánchez-Barriga and Oliver Rader at Bessy II in Germany. I thank Yushiyuki Ohtsubo, Bertran François and Amina Taleb-Ibrahimi at Soleil in France. I thank Koji Miyamoto and Prof. Taichi Okuda-sensei at the Hisor in Hiroshima University in Japan. I thank Ishida Yukiyaki, Takeshi Kondo and Prof. Shik Shin-sensei at the ISSP at the University of Tokyo in Japan. None of this work would be possible without our sample growth and first-principles band structure calculation collaborators. I was truly lucky to work with a number of sample growth groups, and their hard work produced so many high quality samples. These samples were breakthroughs in solid state chemistry and physics. I thank Prof. Bob Cava and his world-renowned team in Princeton Chemistry for single crystal samples. I thank Anthony Richardella and Prof. Nitin Samarth in Penn state for the MBE film samples. I also thank Raman Sankar and Prof. Fangcheng Chou in National Taiwan University and Prof. Shuang Jia’s group in Peking University for single crystal samples. I thank Hsin Lin at National University of Singapore, Tay-Rong Chang and Horng-Tay Jeng at National Tsing Hua University, Cheng-Yi Huang and Wei-Feng Tsai at National Sun Yat-Sen University, and Prof. Arun Bansil at Northeastern University for their collaboration on first-principle calculations. They were always ready to help and sent calculation results on short notices. The timely response from our sample growth and theoretical calculation collaborators was crucially important in our competitive research. I have also been very fortunate to be able to learn from world-renowned scientists at Princeton Physics. I thank Chen Fang for all the discussions we had in his office, at lunch or dinner, while we were walking from the parking lot to the department or at so many random places and random times where we suddenly had some inspiration. Chen almost single-handedly taught me the physics of topological phases beyond Z2 topological insulators. The discussions with him led to many fruitful ideas and new results. I thank Prof. Phuan Ong for agreeing to be second reader on my thesis and for his kind advice. And I thank Prof. Jason Petta and members of his group from whom I learned a great deal during my experimental project. Only people who have experienced the “synchrotron life” would understand the meaning of “constant night shifts”. I cannot imagine myself going through all the physical and mental hard times without my friends. I thank my Princeton friends Jingke Xu, Bo Yang, Jun Xiong, Ke Wang, Zhizhen Zhao, and many others. I also thank my friends back in China. Especially I want to thank Hei (Liang Zhang) for being an honest, generous, reliable friend, for bearing my complaints, for comforting my pains, and for sharing my happiness. I thank my sister Chujun. Wherever she is and however the world changes, I wish her happiness in her life. I thank Cindy for her wonderful cooking during “the SF time”. I thank Jingjing and Tian for their accompany and education. I thank my angel girl momo for her warm care, for her positive thinking and encouragement, and for always sticking with me to share my thoughts and feelings. Finally but most importantly, I am extremely grateful to my family, my grandparents Ruizhi and Ruilan, my mom Xiaobei, my dad Yuping, my aunt Hong, and all family members for all their selfless love and care. Family is my forever source of viii happiness. Contents Abstract . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii Acknowledgements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vi 1 Introduction 1 1.1 The band insulator state and the band inversion . . . . . . . . . . . . 1 1.2 Previously discovered topological phases. . . . . . . . . . . . . . . . . 5 1.2.1 The integer quantum Hall state and the Chern insulator state 5 1.2.2 The 2D Z2 topological insulator - the quantum spin Hall insulator 7 1.2.3 The 3D Z2 topological insulator . . . . . . . . . . . . . . . . . 11 1.3 Theoretical formulations . . . . . . . . . . . . . . . . . . . . . . . . . 21 1.3.1 The Chern number . . . . . . . . . . . . . . . . . . . . . . . . 22 1.3.2 The Z2 topological invariant in two-dimensions . . . . . . . . 22 1.3.3 The Z2 topological invariants in three-dimensions . . . . . . . 23 1.4 Inspiration for discovering new topological phases . . . . . . . . . . . 24 1.4.1 Band inversions and spin-orbit interactions . . . . . . . . . . . 24 1.4.2 Constructing new topological phases . . . . . . . . . . . . . . 27 2 Experimental techniques 31 2.1 Spin-integrated Angle-resolved photoemission spectroscopy . . . . . . 31 2.2 Spin-Resolved Angle-resolved photoemission spectroscopy . . . . . . . 34 2.2.1 Mott polarimetry . . . . . . . . . . . . . . . . . . . . . . . . . x 36 CONTENTS 2.2.2 VLEED . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 2.3 Sample preparation for ARPES . . . . . . . . . . . . . . . . . . . . . 42 2.3.1 Single crystal bulk samples . . . . . . . . . . . . . . . . . . . . 42 2.3.2 MBE film samples . . . . . . . . . . . . . . . . . . . . . . . . 43 2.4 Probing the topological number in 3D bulk materials . . . . . . . . . 45 2.4.1 Separation of insulating bulk from metallic surface states using incident photon energy modulated ARPES . . . . . . . . . . . 2.4.2 45 Surface Dirac crossing, surface-bulk connectivity, and spin-momentum locking . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Topological Quantum Phase Transition in BiTl(S1−δ Seδ )2 47 52 3.1 Evolution of the electronic groudstate across a topological quantum phase transition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 3.2 Topological quantum phase transition in BiTl(S1−δ Seδ )2 . . . . . . . . 56 3.2.1 Identifying a suitable topological material system . . . . . . . 56 3.2.2 Topological quantum phase transition in BiTl(S1−δ Seδ )2 . . . . 58 3.2.3 Spin-orbit coupling vs. lattice constant . . . . . . . . . . . . . 64 3.2.4 3D Dirac semimetal state at the critical point . . . . . . . . . 66 3.3 Topological-critical-point and the “preformed” surface states . . . . . 68 3.4 Topological phase transition and “preformed” critical behavior in (Bi1−δ Inδ )2 Se3 82 4 Topological Crystalline Insulator Phase in Pb1−δ Snδ Te(Se) 84 4.1 Key theoretical concepts for a topological crystalline insulator state . 85 4.2 Discovery of mirror symmetry protected TCI state in Pb1−δ Snδ Te . . 89 4.2.1 Band inversions and mirror symmetries in Pb1−δ Snδ Te . . . . 89 4.2.2 Topological surface states in Pb0.6 Sn0.4 Te . . . . . . . . . . . . 91 4.2.3 Mirror Chern number and mirror symmetry protection . . . . 98 4.3 Topological surface states in Pbδ Sn1−δ Se . . . . . . . . . . . . . . . . 103 CONTENTS 4.3.1 Lifshitz transition and saddle point singularities . . . . . . . . 103 4.3.2 Temperature-driven topological phase transition . . . . . . . . 108 4.3.3 Topological phase diagram in Pb1−δ Snδ Se . . . . . . . . . . . . 111 5 Topological Dirac semimetal state in Cd3 As2 and Na3 Bi 114 5.1 Theoretical concepts for a topological Dirac semimetal . . . . . . . . 116 5.2 3D Dirac semimetal state in high mobility Cd3 As2 . . . . . . . . . . . 121 5.3 Fermi arc surface states in topological Dirac semimetal Na3 Bi . . . . 132 5.3.1 Choice of the surface termination to observe FASS . . . . . . . 132 5.3.2 Observation of Fermi arc surface states in Na3 Bi . . . . . . . . 135 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi . . . . . . 141 5.4 Topological semimetals: Dirac, Weyl, and nodal-line . . . . . . . . . . 150 6 Topological states in 4f Kondo systems SmB6 and YbB6 156 6.1 Observation of surface states in topological Kondo insulator candidate SmB6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157 6.2 Topological surface states in YbB6 . . . . . . . . . . . . . . . . . . . 166 7 A route to 2D topological superconductivity 7.1 Hedgehog spin texture in a magnetic topological insulator 174 . . . . . . 175 7.2 Helical Cooper pairing in topological insulator/superconductor heterostructures Appendices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189 232 xii Chapter 1 Introduction In this chapter, we give an introduction about how a topological phase can arise from a conventional material via the band inversion process. We then briefly review the research works that discovered the first topological phases (the quantum Hall states, and the 2D and 3D Z2 topological insulator states). We try to avoid bringing in many theoretical formulations or experimental details but explain in an intuitive way. After all, there have already been a number of reviews and books that systematically describe the detailed theoretical formations or the experimental details. The spirit here is to highlight the physical picture. In the third section, we provide the theoretical formulations for various topological phases. In the last section of this chapter, we elaborate how these previous works inspire us to search and discover new topological phases of matter. 1.1 The band insulator state and the band inversion The insulating state is one of the elemental groundstates for solids [1–18]. According to band theory, an insulator is described by a set of completely filled electronic bands 1 1.1 THE BAND INSULATOR STATE AND THE BAND INVERSION (known as the valence bands) that are separated from a completely empty set of bands (the valence bands) by an energy gap. An insulator is electronically inert because it takes a finite energy to dislodge an electron. Let us take a representative example an atomic insulator, such as a solid argon. Argon is a noble gas element characterized by a “full shell” atomic structure 3s2 3p6 . As argon atoms crystalize into a solid at low temperatures, the filled 3p6 orbital forms the lowest valence band, whereas the empty 4s orbital forms the lowest conduction band, respectively. These two bands are found to be separated by a large band-gap (∼ 12 eV), and therefore solid argon is a nearly ideal conventional band insulator. Similarly, sodium chloride (NaCl) is a well-known ionic salt. The one electron in the Na 3s1 orbital is lost to the Cl 3p7 orbital, making both Na+ and Cl− ions full shell. And in this case, the filled Cl− 3p orbital and the empty Na+ 3s orbital form the lowest conduction and valence bands. Although insulators can arise from various chemical bonding origins, all these well known conventional band insulators belong to the same topologically trivial phase as the vacuum. This can be conceptually visualized by the following: 1) Take any conventional insulator, e.g. NaCl, and adiabatically change its Hamiltonian to an atomic insulator (solid argon). This process can be viewed as merely changing the energy gap value at each k point without closing the energy gap. 2) Furthermore, with the atomic insulator solid argon, one could imagine increasing its lattice constant (the distance between the nearest two argon atoms) to infinity, which results in a number of unbound argon atoms (the atomic limit, or loosely speaking, the vacuum). Following this conceptual picture, a very interesting question is ”Are all the insulating states topologically equivalent to the vacuum (the atomic limit)?” The answer is no. And those, which are topologically nonequivalent to the vacuum, are the fascinating topological phases of matter. How do we construct a topologically nontrivial phase? The above conceptual picture inspires us to define a “band inversion”. A band inversion is a phenomenon in 2 Figure 1.1: The band insulator state and the band inversion . (a) The crystal structure of a solid argon lattice. (b) The energy levels of a solid argon in the atomic limit where the lattice constant goes to infinity resulting in a number of unbound argon atoms. (c) As the lattice constant goes to the experimental value, the Ar3p and Ar4s orbitals bceome Bloch bands where they gain energy dispersion as a function of the Bloch momentum k. (d) First-principles calculation of the electronic band structure of a solid argon, where the Ar3p valence band, Ar4s conduction band, and the normal band-gap are seen. (e-h) The same as Panels (a-d) but for a topologically nontrivial band insulator Bi2 Se3 . In this case, the relative energy positions of the conduction and valence bands are reversed with respect to their atomic limit (indicated by the blue and red color code in Panels (f,g). This results in a topologically nontrivial state in Bi2 Se3 . In Panel (h), a single Dirac cone surface state (red line) enclosing the Γ̄ within the bulk energy gap is seen. 1.1 THE BAND INSULATOR STATE AND THE BAND INVERSION the electronic structure where the relative energy positions between the conduction and valence bands in a solid are reversed with respect to those of in its atomic limit. Therefore, within band theory, any topologically nontrivial state should have a finite number of band inversions, because the ones that do not can be adiabatically tuned into its atomic limit without closing the band-gap. Now we can understand both a conventional band insulator and a topologically nontrivial insulator under the same band inversion picture: Let us take an insulator and increase the lattice constant to infinity. This will result in a number of unbound atoms or ions. We compare the energy levels for all the filled and unfilled orbitals, and label the last filled orbital as “V” and the first unfilled orbital as “C”, since these two will form the conduction and valence bands in the actual compound. Now we gradually change the lattice constant from infinity to the experimental value, each atomic level will form a Bloch band and gain dispersion as a function of Bloch momentum k. For a conventional band insulator, the energy of the valence band “V” will always remain lower than that of the conduction band “C” at all k points throughout the Brillouin zone (BZ). Therefore, a conventional band insulator is topologically trivial. In contrast, for a topological insulator, the energy of “V” becomes higher than that of “C” at some k points. In this case, in order to restore the relative energy order between “V” and “C” as in the atomic limit, one has to close the bulk band-gap, which involves a quantum phase transition that demonstrates the topological inequality between a topological insulator and the vacuum. We note that band inversion is a necessary but not a sufficient condition for topological phases. After all, a topological phase is defined by a topological number - a global quantity calculated using the electronic wavefunction throughout the BZ. Thus even if a system has nonzero band inversions, one still needs to evaluate the system’s topological number to confirm its topological nontriviality. Although band inversion cannot rigorously define any topological phase, we found that it is in fact very suggestive in terms of identifying real compounds for 4 new topological states and understanding the topological nature in various topological materials, which are the main goals of the experiments in this thesis. For example in numerical band structure calculations, which serves as a useful guide for experiments, it is usually much easier to identify the band inversion in a material (by computing the bulk band structure at different lattice constant) than calculating the actual topological number (e.g. the Chern number involves an integral of the bulk electronic wavefunction throughout the BZ, which is usually impractical to compute). Similarly, experimentally driving a band inversion (by applying pressure, varying temperature or chemical substitution) can drive a conventional material into a topological state or transform an understood topological phase to an unknown and more exotic one by going through a topological quantum phase transition. Therefore, it is in this context that we highlight the importance of band inversion here. 1.2 1.2.1 Previously discovered topological phases. The integer quantum Hall state and the Chern insulator state The experimental discovery of the 2D integer quantum Hall (IQH) state [19] in 1980 marks the first realization of a topological phase of matter. The IQH effect is a quantum version of the Hall effect, which is achieved by applying strong magnetic field in two-dimensional electron systems at low temperatures. In band theory, the quantization of the electrons’ circular orbits leads to quantized Landau levels. The IQH state is an insulator in the bulk because the Fermi level is located in the middle of two Landau levels. On the other hand, the edges of the IQH state feature chiral 1D metallic states, leading to remarkable quantized charge transport phenomena (σxy = ne2 /h) [Fig. 1.2(a)]. It turns out that the key difference between an IQH state and a 2D conventional band insulator is a matter of topology [20–22]. The quantized 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. Figure 1.2: The interface between a quantum Hall state and an insulator has chiral edge mode. (a) The skipping cyclotron orbits. (b) The electronic structure of a semi-infinite edge described in a Chern insulator with a Chern number of n = +1. A single edge state connects the valence band to the conduction band. number n in the transverse magneto-conductivity σxy = ne2 /h is a topological number (the Chern number) that characterizes the nontrivial topology of the IQH state. Two years after the discovery of the IQH effect, the fractional quantum Hall (FQH) effect was observed [23]. The fractional quantum Hall effect (FQHE) is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantized plateaus at fractional values of e2 /h. Unlike the IQH effect, the FQH effect relies fundamentally on electron-electron interactions and therefore cannot be understood in the frame of band theory. It is interesting to note that the FQH effect is not only the second topological state realized in experiments, but also it is believed to have topological order [24]. We will discuss the difference between the topological order and the symmetry-protected topological state later in this section. Let us get back to the IQH state. Since the generators of translations do not commute with one another in a magnetic field, electronic states cannot be labeled with momentum k. Can we construct a quantum Hall like state with a nonzero Chern number but without an external magnetic field so that the system can be understood by the Bloch band theory? The answer is the Chern insulator. The first theoretical model example is the Haldane model [25], where a magnetic field that is zero on the average, but has all of the spatial symmetries of the honeycomb lattice, is 6 1.2.2 The 2D Z2 topological insulator - the quantum spin Hall insulator applied to graphene. And Haldane showed that although the average magnetic field is zero, it opens up a gap at the Dirac nodes of graphene, and furthermore this gapped state is not an ordinary insulator, but rather has a quantized Hall conductivity (a nonzero Chern number). More recently, the Chern insulator state is also theoretically predicted in the magnetically doped thin film of a 3D Z2 topological insulator [9], where no external magnetic field is required and the time-reversal symmetry breaking is provided by the magnetization of the sample itself. We note that such type of Chern insulator is also referred as a quantum anomalous Hall insulator, and it was recently experimentally realized in Cr-doped (Bi1−x Sbx )2 Te3 thin films [9]. One important consequence of the Chern insulator is that now we can understand it in a band theory picture again. As shown in Fig. 1.2(b), a Chern insulator can be understood as a single edge state that connects the valence band to the conduction band. 1.2.2 The 2D Z2 topological insulator - the quantum spin Hall insulator Although a Chern insulator does not require external magnetic field, its internal magnetization still breaks time-reversal symmetry. Can we construct a topological phase that respects time-reversal symmetry? This is particularly motivated by the fact that there are many more time-reversal invariant materials than the time-reversal breaking ones in nature. Such motivation leads to the theoretical prediction of the third type of topological insulator - the quantum spin Hall (QSH) insulator [26, 27]. In a QSH insulator, the bulk is insulating and features a pair of counter-propagating edgestates, which are related by time-reversal symmetry. And the whole system, unlike a Chern insulator, respects time-reversal symmetry. We provide a physical picture to build a quantum spin Hall insulator from two Chern insulators: Let us take a Chern insulator with a Chern number of n = +1, which is achieved by an out-ofplane magnetization +M [Fig. 1.3(a,b)]. Under time-reversal operation T , quantities 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. Figure 1.3: A quantum spin Hall insulator can be constructed by two Chern insulators that are related by the time-reversal symmetry. (a) A Chern insulator with a Chern number of n = +1 has a chiral edge mode as a result of an out-of-plane magnetization. (b) The bottom edge projection of the electronic structure the n = +1 Chern insulator. (c,d,) Same as Panels (a,b) but with a time-reversal operation onto the system. (e,f,) A quantum spin Hall state can be obtained by combining the above-two Chern insulator states. The resulting electronic structure on the edges is described by two couterpropagating edge modes that cross each other at k = 0 (or k = π). The crossing is protected by the time-reversal symmetry as a result of the Kramers theorem. 8 1.2.2 The 2D Z2 topological insulator - the quantum spin Hall insulator including momentum k, angular momentum (including spin σ), magnitization M will change sign. The resulting system after time-reversal transformation is shown in Fig. 1.3(c,d), where a Chern insulator with a Chern number of n = −1 is obtained. Now if one imagines combining these two Chern insulators into a single system, the total magnetization goes to zero, and the system is invariant under time-reversal operation. On the edges of this new system, there are two edge states that are counter-propagating. We draw the electronic structure that is projected to the bottom edge. Since the two Chern insulators are symmetric over time-reversal operation, in the combined system, the two edge modes must “meet” each other at k = 0. In general, as two states cross, they will hybridize and open up a gap. However, in this case, these two edge states that have opposite quantum numbers (Left moving: +k and ↑; Right moving: −k and ↓;) are directly linked by the time-reversal operation because they cross each other at k = 0, a time-reversal invariant momentum (TRIM) (also referred as a Kramers point) [Fig. 1.3(e,f)]. A Kramers point kKramers is defined ~ − kKramers , where G ~ is any reciprocal lattice vector. The Kramers as kKramers = G theorem states that the electronic states have to remain doubly degenerate at the Kramers points in a time-reversal invariant system. And therefore the edge state crossing at k = 0 is protected by the time-reversal symmetry, giving rise to the quantum spin Hall phase. From the above pictures, it is evident that the quantum spin Hall phase is topologically distinct from the vacuum. This is because it is not possible to remove the metallic edge states from the band-gap as long as the edge band-crossing remains intact. The topological nontriviality indicates that there exist a finite number of bulk band inversions at the Kramers points of the BZ. In a real QSH system, no magnetization is present unlike in our conceptual picture. Thus one has to identify a physical interaction that can lead to an inverted band-gap in a time-reversal invariant condition. It turns out that the spin-orbit interaction in heavy elements plays such a critical role. On the other hand, since spin-orbit interaction 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. mixes the spin and orbital degrees of freedom, the physical spin is not a quantum number. Thus it is more correct to think of the “spin” in the quantum spin Hall state in strongly spin-orbit coupled systems as the pseudo-spin rather than the real spin. In 2005, theoretical advances realized that the quantum spin Hall phase is indeed topologically nontrivial [26]. In fact, it is characterized by a new topological number, the Z2 invariant (ν) [14, 26, 29]. The Z2 invariant can only take two values, 0 or 1, where ν = 0 (1) is topologically trivial (nontrivial). In 2007, the QSH phase was experimentally demonstrated in the (Hg,Cd)Te quantum wells using charge transport by measuring a longitudinal conductance of about 2e2 /h (two copies of quantum Hall currents) at mK temperatures [28]. However, no spin polarization was measured in this experiment thus spin momentum locking, which is essential for the Z2 topological physics, was not experimentally observed [28]. It is important to note that the 2D topological (IQH, FQH, and QSH) insulators have only been realized at buried interfaces of ultraclean semiconductor heterostructures at very low temperatures to date. Furthermore, their metallic edge states can only be probed by the charge transport method. These facts hinder the systematic studies of many of their important properties, such as their electronic structure, spin polarization texture, tunneling properties, optical properties, as well as their responses under heterostructuring or interfacing with broken symmetry states. For example, the two counter-propagating edge modes in a QSH insulator are predicted to feature a 1D (usually Dirac) band crossing in energy and momentum space. And edge mode moving along the +k direction is expected to carry the opposite spin polarization as compared to that of one moving in the −k direction. However, neither the Dirac band crossing nor the spin-momentum locking of the edge modes in a QSH insulator are experimentally observed, due to the lack of experimental probe that can measure these key properties for a 1D edge mode at a buried interface at mK temperatures. 10 1.2.3 The 3D Z2 topological insulator 1.2.3 The 3D Z2 topological insulator In 2007, it was theoretically realized that the Z2 topological number in a QSH insulator can be generalized to three-dimensions, thus realizing the first three-dimensional topological phase of matter [14–18]. This is again a critical breakthrough in experimental and material physics because there are more 3D bulk materials than 2D films in nature and the preparation of bulk materials is usually easier. How do we construct a 3D Z2 TI? The most straightforward approach is to simply stack a number of uncoupled 2D quantum spin Hall states to form a 3D bulk. It turns out that such simple stacking of the 2D QSH states does lead to a type of 3D Z2 TI, which is the so called 3D weak TI. A weak TI is not the most topologically protected Z2 nontrivial states in bulk materials. But let us start from a weak TI. As shown in Fig. 1.4, let us assume that we start from a 2D QSH state that has an inverted band-gap at the Γ point. The blue and green colors in Fig. 1.4(a) show the orbital nature of the bulk bands near the Γ point, where a band inversion is evident. Now let us have N copies of such QSH state and stack them along the out-of-plane ẑ direction. This will form a bulk material. And in momentum space, it means that the 2D BZ will gain periodicity in the kz direction and becomes a cube representing the 3D BZ [Fig. 1.4(b)]. In the 3D BZ, the Kramers points can be sorted by their origins from the 2D BZ before stacking. For example, both the Γ and the Z points in the 3D BZ results from the Γ point in the 2D BZ. We assume that the physical coupling between these 2D QSH slices are extremely weak (e.g. in real materials, imagine they are coupled by a very weak van der Waals interaction). This means that the energy dispersion along the kz direction is sufficiently weak, so that it does not change the orbital nature of the conduction and valence bands by going from the Γ(3D) point to the Z point. Therefore, the one band inversion in the 2D Γ point in the QSH slice becomes two band inversions at both the Γ and the Z points in the 3D BZ after stacking (here only the band inversions at the Kramers points are counted). 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. Figure 1.4: A 3D weak topological insulator can be obtained by stacking N copies of identical 2D quantum spin Hall states along the out-of-plane direction. (a) A 2D quantum spin Hall state where there is a band inversion at the 2D BZ center Γ point. (b) stacking N copies of such quantum spin Hall slices along the out-of-plane direction form a bulk material. In momentum space, it means that the 2D BZ will gain periodicity in the kz direction and becomes a cube representing the 3D BZ. The time-reversal invariant momenta in the 3D BZ are noted. (c) Before turning on the inter-slice coupling, different QSH slices are completely identical and idenpendent (e.g. Cut2 and Cut3). This also means that there is no energy dispersion along the out-of-plane Γ − Z direction (Cut1) (d) A finite (but weak) inter-slice coupling means that the states in the QSH system gain energy dispersion along the out-of-plane kz direction. The inter-slice coupling is weak enough, so that it does not change the orbital nature of the conduction and valence bands by going from the Γ(3D) point to the Z point (Cut1). Therefore, there are two band inversions at both the Γ and the Z points in the 3D BZ (Cuts 2 and 3). 12 1.2.3 The 3D Z2 topological insulator Figure 1.5: The surface of a weak TI shows even number of protected surface states or no surface states depending on the surface termination. (a) A bulk BZ of the weak TI. The green slices are chosen for detailed studies. (b) The edge projected electronic structure for the green slices shown in Panel (a). Without any inter-slice coupling, these slices are identical and independent. The surface states for the kx − kz surface projection is a straight line. (c) A bulk BZ showing the two band inversions at the Γ and the Z points. (d) After turning on the inter-slice coupling, the edge states can hybridize and open out gaps, except at the Γ and the Z points due to the protection of the time-reversal symmetry. Therefore, the surface state Fermi surface is described by two dots at the Γ and the Z points. 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. What about the edge states of each QSH slice? Let us look at a few representative QSH slices at different kz values as shown by the green 2D slices in Fig. 1.5(a). As seen in Fig. 1.5(b), before we turn on the coupling between these slices, each slice is a QSH that features two counterpropagating edge modes at its edge. We fix the chemical potential at the crossing point of the edge modes and investigate the kx − kz plane where all the QSH edges are stacked to form a surface. Thus all the 1D edge states from the QSH slices are stacked and become a 2D surface state. The surface state Fermi surface is a straight line that goes from Z − Γ − Z. Now we turn on the inter-slice coupling (hybridization). As we have mentioned above, in general if two edge states cross, they will open up an energy gap. However, at and only at the Γ and the Z points, the edge state crossings are preserved because these two points are the Kramers’ points. Consequently, the surface state Fermi surface of the kx − kz plane becomes two dots at the Γ and the Z points. And if the EF is shifted slightly away from the crossings, then the two Fermi dots will evolve into two circles that enclose the Γ and the Z points, respectively. Therefore, the surface states at the kx −kz plane are described by two surface states that enclose the Γ and the Z points, respectively. In contrast, at the top kx − ky surface, no protected surface state is expected. This is because both Γ and Z points project onto the Γ̄ point of the top kx − ky surface. The two surface states that originate from the band inversions at Γ and Z points can hybridize and open up a gap. Therefore, it can be seen that a weak TI features protected 2D surface states only at certain crystalline surface terminations. In fact, from the topology point of view, the 3D weak TI state is essentially equivalent to a number of independent 2D quantum spin Hall slices, because there involves no band inversion by decomposing a weak TI into uncoupled 2D QSH slices. Can we construct a 3D Z2 TI state that cannot be adiabatically reduced into a bunch of stacked QSH states? Also, from the surface state point of view, a 3D weak TI only has protected surface states at certain surface terminations. Is there a 3D Z2 TI 14 1.2.3 The 3D Z2 topological insulator state that shows protected surface states at all surfaces irrespective of the choice of the termination? The answers for both questions lead to the 3D strong TI phase. Let us again start by stacking QSH slices (Fig. 1.6). It is obvious that a weak inter-slice coupling only leads to the weak TI phase. Now we examine the strong coupling scenario. We know that at the 2D Γ point the conduction and valence bands are inverted with respect to the atomic limit. Without interlayer coupling, it means that there exist two band inversions at both the Γ and the Z points of the 3D BZ. Now we turn on the inter-slice coupling. And in this case, the inter-slice coupling is strong enough and affects the electronic structure in a way so that the band inversion at the Z point is in fact removed [Cut1 in Fig. 1.6(d)]. As shown in the Cuts 2 and 3 in Fig. 1.6(d), while at the Γ point (Cut2) the conduction and valence bands are still inverted with respect to the atomic limit, at the Z point (Cut3) these two bands restore the relative energy positions as in the atomic limit (no band inversion). Therefore, in this case, there is only one band inversion at the Γ point throughout the 3D BZ. This is an example of a 3D strong TI state. It is important to note that the 3D strong TI state is topologically distinct from both the weak TI and the conventional band insulator (the atomic limit) states. This is because (1) it is not possible to reduce the strong TI to uncoupled 2D QSH slices without going through a band inversion at the Z point. Therefore a strong TI is topologically inequivalent to a weak TI. (2) it is also not possible to change a strong TI to a conventional band insulator without going through a band inversion at the Γ point. We now investigate the possible existence of protected surface states in the strong TI state (Fig. 1.7). We note that there is only one band inversion at the Γ point for the strong TI state, and that at any surface termination the Γ point projects onto the surface BZ center Γ̄ point. Therefore, one expects a single surface state enclosing the surface BZ center Γ̄ point at any surface termination. We also note that the case presented here in Figs. 1.6 and 1.7 is only one of the possible ways to generate a strong 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. Figure 1.6: A 3D strong topological insulator can be obtained by coupling N copies of 2D quantum spin Hall states along the out-of-plane direction in a nontrivial way. (a) A 2D quantum spin Hall state where there is a band inversion at the 2D BZ center Γ point. (b) The 3D BZ. The time-reversal invariant momenta in the 3D BZ are noted. (c) Before turning on the inter-slice coupling, there is no energy dispersion along the out-of-plane Γ − Z direction (Cut1). (d) A strong inter-slice coupling can drive a band inversion along the out-of-plane Γ − Z direction (Cut1). In this case, while at the Γ point (Cut2) the conduction and valence bands are still inverted with respect to the atomic limit, at the Z point (Cut3) these two bands restore the atomic limit (no band inversion). Therefore, there is only one band inversion at the Γ point of the 3D BZ. 16 1.2.3 The 3D Z2 topological insulator TI. In general, a strong TI should always possess an odd number of band inversions at the Kramers’ points in a 3D BZ, but the exact number of band inversions (1, 3, 5, or other odd numbers) depends on the exact form of the inter-slice coupling as well as the properties of the 2D QSH state to start with (e.g. one can also imagine to have a QSH state with a band inversion at the 2D BZ corner M point not the Γ point). However, regardless of these details, a strong TI will always have an odd number of band inversions in the bulk and feature an odd number of surface states enclosing the Kramers points irrespective of the surface termination. It is also important to note that the surface state of 3D TIs are usually referred as “Dirac cone” surface states in many research works. “Dirac cone” means that the surface states cross at the Kramers point with a linear dispersion. This is, however, not always true. In fact, the Kramers theorem only requires the surface states to remain doubly degenerate at a Kramers point, or, in other words, the surface states have to cross each other at the Kramers point. But it does not require a specific fashion of the crossing in terms of the energy dispersion of the surface states. It is actually also possible to have surface states with cubic or even higher order crossings in principle. But a cubic or high order crossing means that the linear term is somehow forbidden due to the presence of certain additional symmetry. This is quite hard and it has not been experimentally achieved yet. Therefore, “Dirac” surface state is usually used to describe the metallic boundary mode of 3D strong or weak TIs. The above physical pictures can be mathematically formulated, which results in the Z2 topological numbers for a 3D bulk system [14–16,29]. In 2007, it was theoretically realized that in three-dimensions, there exist four Z2 topological invariants that define the topological property of a 3D bulk material, namely (ν0 ; ν1 ν2 ν3 ), where ν0 is the strong topological invariant, and ν1 − ν3 are the weak topological invariants, respectively [14]. If all four invariants are zero, then the system is a conventional band insulator. If the strong invariant ν0 = 0 but one or more than one of the weak 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. Figure 1.7: The surface of a strong TI features an odd number of protected surface states at all surfaces irrespective of the surface termination. (a) A bulk BZ of the strong TI. The green slices are chosen for detailed studies. (b) The edge projected electronic structure for the green slices shown in Panel (a). Without any inter-slice coupling, these slices are identical and independent. The surface states for the kx − kz surface projection is a straight line. (c) A bulk BZ showing the one band inversion at the Γ point. (d) After turning on the inter-slice coupling, in the case of a strong TI, only the band inversion at the Γ point remains whereas the band inversion at the Z point is removed. Furthermore, for k−space region near the Γ point where the conduction and valence bands are inverted, the edge states can hybridize and open out gaps, except at the Γ point itself due to the protection of the time-reversal symmetry. Therefore, the surface state Fermi surface is described by one dots at the Γ point. 18 1.2.3 The 3D Z2 topological insulator invariants is nonzero (ν1 + ν2 + ν3 6= 0), then the system is a weak TI. Finally, if the strong topological invariant is nonzero (ν0 = 1), the system is a 3D strong Z2 topological insulator. Experimentally, in 2007, the 3D strong TI phase was experimentally identified in the Bi1−x Sbx semiconducting alloy system, marking the first realization of a topologically nontrivial phase of matter in 3D bulk materials [30, 31]. Shortly after Bi1−x Sbx , another class of strong TI - the Bi2 Se3 class - was experimentally discovered [32–36]. The Bi2 Se3 class was found to feature a single Dirac cone surface state due to a single bulk band inversion at the Γ point (same as the example given in Figs. 1.6 and 1.7) and therefore it serves as the prototype 3D TI, which has been the most widely researched topological insulator even to date. More importantly, it turns out that the experimental discovery of the 3D topological insulator phase in 2007 opened a new experimental era in fundamental topological physics [30–128]. In contrast to its 2D analogs, (1) a 3D topological insulator can be realized at room temperatures without magnetic fields. Their metallic surface states exist at bare surfaces rather than only at buried interfaces. (2) The electronic and spin groundstate of the topological surface states can be systematically studied by spin- and angle-resolved photoemission spectroscopy (spin-ARPES), which provides a unique and powerful method for probing the topological number in three-dimensional topological phases. (3) Due to the accessible conditions (room temperature, no magnetic field, bare surface), it is also possible to study the tunneling [88–95], electrical transport [96–107], optical [108–115], and many other key properties of the topological surface states. (4) The 3D topological insulator materials can be doped or interfaced to realize superconductivity or magnetism [53–61]. (5) Since its discovery in 2007, there have been more than a hundred compounds identified as 3D Z2 topological insulators. These conditions not only make the 3D Z2 TI state a topic of huge research interest worldwide, but also lay the experimental foundation for discover- 1.2 PREVIOUSLY DISCOVERED TOPOLOGICAL PHASES. ing new topological phases of matter [37–45, 47–52], which is the main theme of this thesis. We note that time-reversal symmetry is required for a Z2 topological insulator phase. This can be visualized in the surface state point of view. If time-reversal symmetry is broken, the surface state degeneracy at the Kramers point can be lifted. And in that case, the distinction between a Z2 topological insulator and a conventional band insulator no longer exists. In the topological theory, a state that is topologically nontrivial only if a symmetry is respected is called a symmetry protected topological (SPT) state. A Z2 TI is a SPT state [129]. On the other hand, a state whose topological nontriviality does not rely on any additional symmetry is defined as a state that features topological order [24]. In general, the realization of a topological order inherently requires strong electron-electron interaction, which is beyond band theory [24]. Strong interaction leads to fractionalized non-electron-like quasi-particle boundary excitations, which is believed to be one of the key properties for a system with a topological order. A fractional quantum Hall (FQH) state, whose edges feature gapless excitations with fractional charges, is an example of a state with a nontrivial topological order. This is in contrast to the Z2 TI phase (a SPT state) where the metallic surface states are electron quasi-particles. In theory, it is believed that the boundary modes in a state with topological order can be robust against any local perturbation, whereas the gapless boundary modes in a SPT state are robust against local perturbations that do not break the corresponding symmetry. It is in this sense that a state with topological order is more robust than a SPT state. However, let us also view this issue based on experimental and material facts. Due to the requirement of very strong electron-electron interaction, topological order is more difficult to realize and its existence is rarer in real solid-state materials as compared to a SPT state. As a matter of fact, the FQH state is the only state with topological order that has been experimental realized so far. Other theoretical proposals, such as 20 a fractionalized Chern insulator [130], or a fractionalized topological insulator [131], etc., remain elusive due to the difficulty of identifying a real system that has the necessary material parameters. Moreover, the experimental study of a topological phase relies on measuring its gapless boundary states. In a topologically ordered state, the boundary modes are fractionalized non-electron like quasi-particles. Although in the case of FQH, their existence can be demonstrated by charge transport. But it is in general extremely challenging to systematically study the energy dispersion, angular momentum (spin polarization), and other key properties of fractionalized non-eletronlike quasiparticles. On the other hand, these difficulties do not exist in a SPT state such as a Z2 TI state in Bi2 Se3 . Furthermore, the requirement of a symmetry in a SPT state is usually a “given” in a solid state system. For example, in a solidstate crystal, the translational symmetry or sometimes also space group symmetries (mirror, Cn ) is a given. Furthermore, time-reversal symmetry is also a very common property that exists in most non-magnetic materials. In fact, in experiments, it is quite often that one has to make considerable effort to break a certain symmetry (e.g. to apply strong magnetic field to break time-reversal symmetry for a FQH state) in order to realize certain topological order. Therefore, by these (experimental or material) considerations, the realization, the systematic study and the utilization of SPT states are of importance and interest. In this thesis, we focus on the experimental discoveries of new symmetry-protected topological states (mostly weakly interacting systems within the band theory) beyond a Z2 TI. 1.3 Theoretical formulations In this section, we provide the theoretical formulations for the Chern number and the Z2 invariants. 1.3 THEORETICAL FORMULATIONS 1.3.1 The Chern number In the IQH effect, the quantized Hall conductivity can be written as σxy = ne2 /h, where n is an integer. Thouless, Kohmoto, Nightingale and den Niks (TKNN) found that the integer n in the transverse magneto- conductance σxy is precisely the Chern number - a topological number calculated using the electronic wavefunction over the entire Brillouin zone. Specifically, the Chern number in the IQH state in a periodic potential is written as [21]: 1 n= 2π Z BZ [∇k × A(kx , ky )]z d2 k (1.1) with A = −i < u(k)|∇|u(k) > (1.2) One important consequence is that because A(k) is odd under time-reversal, σxy must vanish if the 2D system respects time-reversal symmetry. This is consistent with what we show in the previous section that both the IQH and the Chern insulator states break time-reversal symmetry. 1.3.2 The Z2 topological invariant in two-dimensions There are several mathematical formulations of the Z2 invariant ν, including a Pfaffian construction, as a topological obstruction, as a type of pumping, or in terms of homotopy of Hamiltonian spaces [7]. We take the Pfaffian approach developed by Fu, Kane and Mele [14]. We define a unitary matrix: ωmn (k) =< um (k)|Θ|un (−k) > (1.3) where |um > is the occupied wavefunction, Θ is the time-reversal operator. Since Θ is anti-unitary and Θ2 = −1, thus ω T (k) = −ω(−k). There are four special points 22 1.3.3 The Z2 topological invariants in three-dimensions Λa in the bulk 2D BZ, where k and −k coincide. In the square 2D BZ as shown in Fig. 1.4(a), these four points are the Kramers points, namely 1 Γ, 2 X, and 1 M. At these four points, ω(Λ) is antisymmetric. The determinant of an antisymmetric matrix is the square of its pfaffian (P f ), which allows us to define p δa = P f [ω(Λa)]/ Det[ω(Λa )] = ±1 (1.4) Provided the Bloch wavefunction |um(k) > is chosen continuously throughout the Brillouin zone (which is always possible), the branch of the square root can be specified globally, and the Z2 invariant is ν (−1) = 4 Y δa (1.5) a=1 If the crystal has inversion symmetry, there exists a shortcut to obtain ν [29]. At the Kramers points Λa the Bloch states um (Λa ) are also the eigenstates of the parity operator with the eigenvalue ξm (Λa ) = ±1. The Z2 invariant then simply follows from with δa = Y ξm (Λa ) (1.6) m where the product is over the Kramers pairs of occupied bands. This has proven quite useful for identifying Z2 topological insulators from numerical band structure calculations. 1.3.3 The Z2 topological invariants in three-dimensions In three dimensions there are eight Kramers points, which are expressed in terms of primitive reciprocal lattice vectors as Λa = (n1 b1 + n2 b2 + n3 b3 )/2, with n = 0, 1. This leads to four independent Z2 topological invariants to define the Z2 topological 1.4 INSPIRATION FOR DISCOVERING NEW TOPOLOGICAL PHASES properties of a 3D band insulator, namely [ν0 ; ν1 ν2 ν3 ], where ν0 is the strong invariant and (ν1 , ν2 , ν3 ) are the weak invariants. The strong invariant can be calculated by the pfaffian over all eight Kramers points (−1)ν0 = 8 Y δa (1.7) a=1 where again we have δa = P f [ω(Λa)]/ p Det[ω(Λa)] = ±1. Besides the strong invariant, it has been shown in theory that one can define another 3 independent weak invariants (ν1 , ν2 , ν3 ) as (−1) νi =1,2,3 = 8 Y δa . (1.8) ni =1;nj 6=i=0,1 Again, the conclusion from the above topological theory is that if all four invariants are zero (ν0 = ν1 = ν2 = ν3 = 0), then the system is a conventional band insulator; if ν0 = 1, then the system is a strong (Z2 ) topological insulator; if ν0 = 1 but at least one of the weak invariants is nonzero, then the system is a weak (Z2 ) topological insulator. 1.4 Inspiration for discovering new topological phases Now that we have gone through all previous topological phases, we discuss the inspirations that are brought by these previous works for discovering new topological matter. 1.4.1 Band inversions and spin-orbit interactions First of all, it is evident that the band inversion is a key (a critical necessary condition) that gives rise to the topological insulator state. More specifically, by band inversion, we mean two phenomena in the bulk electronic structure: (1) At certain k points, the 24 1.4.1 Band inversions and spin-orbit interactions relative energy positions between the conduction and the valence bands are reversed with respect to those of in the atomic limit. (2) An insulating gap is opened once the conduction and valence bands are inverted. How do we realize a band inversion with these two phenomena in real materials? Is there any clue or hint regarding how to search for materials with band inversions? Let us again start from a very simple case, which is NaCl (an ionic insulator). We write it as Na+ Cl− to highlight the distinct ionic states of sodium and chlorine in this insulator. As shown in Fig. 1.8, the lowest valence and conduction bands near the Fermi level are the Cl− 3p and the Na+ 3s orbitals, respectively. As the system goes from the atomic limit [Fig. 1.8(a)] to the actual lattice constant [Fig. 1.8(b)], these bands gain energy dispersion as a function of Bloch momentum k. In the case of Na+ Cl− , the relative energy positions between the conduction and valence bands remain the same as the atomic limit at all k points throughout the BZ. Thus a large full band-gap is formed. The physical meaning of the band-gap can be understood in the picture that it costs a finite amount of energy (∼ the band-gap) to excite an electron from the valence band to the conduction band, or more loosely speaking, to give the electron that is transferred to Cl− back to the Na+ [Fig. 1.8(c)]. Such a process is highly energetically unfavorable because the system gains much energy as Na atom transfers its 3s1 electron to the Cl atom to form Na+ Cl− . Now let us imagine another compound A+ B− , where we label the lowest valence and conduction bands as B− and A+ , respectively as shown in Fig. 1.8(d). Now as we tune the lattice constant to the actual value, the valence and conduction bands gain energy dispersion in a way so that these two bands actually cross at certain Kramers point, as shown in Fig. 1.8(e). Now in this scenario, at the k−space vicinity to the Kramers point where band-crossing occurs, the system actually gains energy to give the electron that is transferred to the B atom back to the A atom. Furthermore, it is important to note that as the conduction and valence bands cross, they become 1.4 INSPIRATION FOR DISCOVERING NEW TOPOLOGICAL PHASES Figure 1.8: Band Inversions and the spin-orbit interaction. (a-c) In the case of sodium chloride Na+ Cl− , the system does not have any band inversion. The fact that there is a large band-gap between the Cl− 3p and the Na+ 3s bands is consistent with that it is energetically costly to give the electron that is taken by the Cl− back to the Na+ . (d-f ) In a material A+ B− , the valence and conduction bands gain energy dispersion in a way so that these two bands actually cross at certain Kramers point. Further consideration of the spin-orbit interaction opens a full insulating gap. SnTe is a real material example for this case. (g-i) In this case, without spin-orbit coupling, there is no band crossing, and the spin-orbit interaction is responsible for both inverting the conduction and valence bands and for opening up the full insulating gap. We note that Bi2 Se3 belongs to this case. 26 1.4.2 Constructing new topological phases degenerate at certain k points in the BZ [see Fig. 1.8(e)]. Thus there does not exist a full insulating gap as required by the Z2 topological insulator state. However, as we further consider the effect of the spin-orbit interaction, it causes the bands that cross to hybridize and open up a full band-gap. In terms of real materials, SnTe is a famous example of this kind [132], where a band inversion between the Sn5p and Te5p orbitals is found even without the including the spin-orbit interaction at each L point of its BZ. And the spin-orbit interaction is responsible for opening up a full band-gap. There is another slightly different case, as shown in Figs. 1.8(g-i), where without spin-orbit coupling, there is no band crossing, and the spin-orbit interaction is responsible for both inverting the conduction and valence bands and for opening up the full insulating gap. We note that Bi2 Se3 belongs to this case [33]. From the above physical picture, it is quite clear that we need to work with materials with heavy (high Z) elements for a strong spin-orbit coupling, which is necessary to open up a full band-gap. Furthermore, it can be seen that we cannot have A+ B− materials like NaCl, where Na strongly prefers to loose an electron and Cl strongly prefers to take an electron. In this case, it is hard to imagine that one could get a band crossing at certain k− points because a band crossing creates a local k− space regime, where it is energetically favorable to return the electron taken by the B− back to the A+ . This means that we should look for materials that are composed of heavy “semimetal” elements. Therefore, bismuth (Bi) is a good candidate because it can form both a positive ion as Bi3+ or Bi5+ , and a negative ion as Bi3− , whose energies are not significantly different. In fact, Bi2 Se3 (Bi3+ ) and Na3 Bi (Bi3− ) are two good examples for the above argument in searching for materials with band inversions. 1.4.2 Constructing new topological phases How do we construct new topological phases? From the discussions in the previous sections, we know that the band inversion is a necessary but not a sufficient condition 1.4 INSPIRATION FOR DISCOVERING NEW TOPOLOGICAL PHASES to realize a topological state. In the case of the Z2 TI state, the argument is that the bulk band inversions occur at the Kramers points of the BZ. Therefore, a surface (edge) state band crossing can be protected by the Kramers theorem. (1) Inspired by this logic, can we find other types of symmetries that can also protect a surface (edge) state band crossing (a doubly degeneracy of the surface bands)? If a symmetry can protect a surface state band crossing at certain momentum space locations in the surface BZ, then we just need to construct a material that has a number of bulk band inversions that locate at these special momentum space locations. In a solid state crystal system, the most common symmetries besides the time-reversal symmetry are the various space group symmetries. In Chapter 4, we will systematically discuss such possibilities, leading to our experimental identification (one of the three concurrent ARPES works) of the first topological crystalline insulator (TCI) phase in the Pb1−x Snx Te(Se) system. (2) In general, in a 3D bulk crystal, if two bands cross each other as shown in Fig. 1.8(e), spin-orbit interaction can cause hybridization between the two bands that cross and open a full energy gap. As two 3D bulk bands cross, they become degenerate at multiple k points in the BZ. Thus a full energy gap means spin-orbit interaction lifts up the degeneracy at all k points where they cross. This is actually quite intuitive because without consideration of extra symmetries, there is no reason a certain k point is more special than other k points where the two bands are degenerate. Therefore, if spin-orbit interaction breaks the degeneracy, it should do that at all bulk band crossing k points. However, this inspires us to ask a question whether we can identify additional symmetries that can protect the bulk band crossings at certain k points even with the consideration of the spin-orbit coupling? If that scenario can be realized, then an important consequence is that the system becomes a semimetal, where the conduction and valence bands have finite overlap and there does not exist a full band-gap 28 1.4.2 Constructing new topological phases irrespective of the choice of the chemical potential. Then an interesting question is whether the system can still be topological if the bulk band gap closes (meaning that there is no full energy gap)? If so, how do we define its topological number and what would the surface state be like? In Chapter 5, we will deal with these intriguing questions, which lead to our experimental realization of the topological Dirac semimetal phase in Cd3 As2 and Na3 Bi. (3) In the case of Bi2 Se3 as shown in Figs. 1.8(g-i), the inverted band gap is solely opened due to the spin-orbit coupling. The effect of electron-electron correlation is negligible. Thus the low energy physics within the inverted band-gap is described by the single-particle picture. Can we find a material where the electron-electron interaction plays a non-negligible role in opening up the inverted bulk band-gap? In Chapter 6, we present our experimental studies on a well-known f -electron system SmB6 . In SmB6 , a narrow (∼ 15 meV) band-gap opens at low temperatures (. 30 K) due to the coherent hybridization between the conduction d electrons and the localized f electrons near the the Fermi level. We show experimental evidence consistent with the existence of topological surface states within the Kondo gap, supporting the existence of a topological Kondo insulator phase in SmB6 . (4) None of the known TI materials (represented by Bi2 Se3 ) are naturally superconductors or magnets. It is of interest to study the interplay between a topological state and a broken-symmetry (superconducting or ferromagnetic) state. In Chapter 7, we present systematic studies of the electronic and spin groundstate of the prototype TI Bi2 Se3 as it is doped into or in proximity to a symmetry-broken (superconducting or magnetic) state. We identify the key experimental signatures in our experiments that are considered as the keys to realizing a topological superconductor or a Chern insulator. (5) Finallly, all the states mentioned above are new (symmetry-protected) topological phases beyond a Z2 TI, which means that they cannot be smoothly deformed 1.4 INSPIRATION FOR DISCOVERING NEW TOPOLOGICAL PHASES into each other without going through a band inversion (a topological quantum phase transition). Can we experimentally realize a band inversion and a topological quantum phase transition? This will bring valuable insights in understanding the way how two states with distinct topological numbers can be turned into each other. In Chapter 3, we present our our experimental realization of a topological quantum phase transition in the BiTl(S1−δ Seδ )2 system, which demonstrates the one of the most basic topological quantum phase transitions - a topological transition between a conventional band insulator and a Z2 topological insulator. 30 Chapter 2 Experimental techniques In this chapter, we introduce the basic principles of the experimental technique used in this thesis (the spin-resolved angle-resolved photoemission spectroscopy) and the review how such technique is used to reveal the 3D Z2 topological insulator state in Bi1−x Sbx and Bi2 Se3 bulk materials. 2.1 Spin-integrated Angle-resolved photoemission spectroscopy Angle-resolved photoemission spectroscopy (ARPES) is a direct experimental technique to observe the distribution of the electrons (more precisely, the density of singleparticle electronic excitations) in the reciprocal space of solids [133, 134]. ARPES is one of the most direct methods of studying the electronic structure of the surface of solids. The photoelectric effect was first observed by Hertz. When photons of energy hν, strike a sample surface, electrons absorb the energy and escape into the vacuum with certain kinetic energies. A good approximation of the photoemission process can be described by the three-step model, as shown in Fig. 2.1: • An electron is first excited by the photon inside the bulk. 31 2.1 SPIN-INTEGRATED ANGLE-RESOLVED PHOTOEMISSION SPECTROSCOPY Figure 2.1: sample. The three-step model used to describe the photoemission process inside the • The excited electron then travels to the sample surface. • The electron escapes from the sample into the vacuum. After a photoelectron comes out of the sample, it is being collected by an electron analyzer, as a function of its kinetic energy as well as the surface emission angles θ and φ (Fig. 2.2). The excited photoelectron then follows the kinematics below which describes the momentum p~ = ~~k 1p 2mEkin sin θ cos θ ~ 1p ky = 2mEkin sin θ sin θ ~ 1p 2mEkin cos θ kz = ~ kx = (2.1) (2.2) (2.3) The conservation of energy gives: Ekin = hν − φ − |EB | (2.4) 32 Figure 2.2: (a) The Scienta analyzer setup used to measure emitted photoelectrons from the sample surface. The two hemispheres probe the electrons to produce a 2D image of energy (E) vs. momentum (k) in one measurements. (b) The geometry of the detector relative to the sample surface. The momentum of the electron inside the sample can be extracted from the measured values of Ekin , θ, φ. 2.2 SPIN-RESOLVED ANGLE-RESOLVED PHOTOEMISSION SPECTROSCOPY where φ is the work function of the sample and EB is the binding energy of the electrons. Due to the existence of a surface potential experienced by the escaping electron, the component of the momentum perpendicular to the sample surface is not conserved. To capture the effect of the surface potential, we assume that the energy of the “real” final state (free from the influence of the surface potential) Ef has an energy offset of V0 with respect to the kinetic energy measured by the analyzer Ekin , namely Ef = Ekin + V0 (2.5) where V0 is usually referred as the inner potential. Since the in-plane momentum is conserved, thus we know that ~kk = Moreover, we know that ~2 k k 2 2m + ~2 k ⊥ 2 2m √ 2mEkin sin θ. = Ef . Therefore, from these relationships, we get: k⊥ = 1p 2m(Ekin cos2 θ + V0 ) ~ (2.6) where V0 is usually referred as the inner potential. The value of V0 can be determined experimentally by measuring the periodicity of the energy dispersion along the out-of-plane momentum k⊥ direction at the normal emission angle. However, for samples where the dispersion perpendicular to the sample surface is small, such a measurement can be difficult. 2.2 Spin-Resolved Angle-resolved photoemission spectroscopy The Spin-Resolved Angle-resolved photoemission spectroscopy not only measures the energy E and the Bloch momentum k but also the spin polarization of an electronic 34 2.2.1 Mott polarimetry state. In this section, we review two currently used techniques for spin-resolved photoemission experiments. To perform spin-resolved electron studies, an electron spectrometer has to be combined with a suitable spin polarimeter. To determine the spin of an ensemble of electrons, one needs to utilize a spin-dependent scattering process. The traditional one is the Mott polarimetry. Such a technique arises from spinorbit interaction of heavy elements (such as gold) that are used as the detector target where a spin polarized electron beam is injected, causing spin-dependent scattering. However, since the spin-orbit interaction is usually a small effect compared to the Coulomb interaction between electrons, the spin dependence for most scattering targets and a wide range of parameters is small. The relative influence of the electron spin on the scattering cross section only becomes significant under conditions, where the mean scattering cross section is small. Thus in general, the efficiency of the Mott polarimetry method is not so high. For example, measuring the spin polarization of the surface state of TI Bi2 Se3 at a fixed energy E along a fixed momentum space direction cut takes about 6 - 8 hours to gain good statistics using the Mott polarimetry with synchrotron radiation light source. A newer technology, the very low energy electron diffraction (VLEED) spin detector was recently applied. A VLEED uses a magnetic scattering target. In electron diffraction on ferromagnets, the intensities of diffracted beams in general depend on the spin polarization of the primary electron beam relative to the sample magnetization. If the incident electron beam has a very low energy (usually < 10 eV), then the efficiency of measuring spin polarization is dramatically improved as compared to a Mott polarimetry. 2.2 SPIN-RESOLVED ANGLE-RESOLVED PHOTOEMISSION SPECTROSCOPY Figure 2.3: Mott polarimetry. Schematic of a Mott scattering geometry. Incident electrons (red dot) with a polarization P~ on a high Z nucleus (yellow dot) are backscattered to the left and right with a probability that is dependent on P~ . The figure is adapted from Ref. [136]. 2.2.1 Mott polarimetry The interaction Hamiltonian between a photon and spin 1 2 electron can be described by the Dirac equation: Hint = 1 e~ e~ 2 ~ + ie~ E ~ · p~ − e~ ~σ · (E ~ × p~) (2.7) + eΦ − (~p − A) ~σ · (▽ × A) 2 2 2m c 2mc 4m c 4m2 c2 ~ is the photon vector potential, Φ is the scalar where ~p is the electron momentum, A ~ is the electric field and ~σ is the electron spin. However by using linearly potential, E polarized photons in the UV to soft x-ray regime, it has been shown ( [135]) that the spin dependent terms are greatly suppressed, and the photon electron interaction e ~ A · p~, Hamiltonian can be well approximated by the Schrodinger model Hint = − mc which conserves spin. Provided the photoemission process is spin-conserving, the spin of the initial state of an electron in a solid can be determined by measuring its spin after it has been photoemitted. Mott electron polarimetry ( [135]) is a method of separating electrons of different spin from such a photoemitted beam based on the use of spin-orbit (Mott) 36 2.2.1 Mott polarimetry scattering of electrons from nuclei. The physical principle of Mott scattering can be understood from the classical picture of a moving electron scattering off of a stationary bare nucleus of charge Ze. At low incident energies, the electron interacts with the nucleus predominantly via its charge, and scattering is described by the Rutherford cross section σR (θ), where the scattering angle θ is typically small. At high incident energies and in cases where Z ~ of the nucleus can result is large, the velocity ~v of the electron in the electric field E ~ in its rest frame given by: in a considerable magnetic field B ~ = − 1 ~v × E ~ B c (2.8) ~ = (Ze/r 3 )~r, can be written as which, using E ~ = Ze ~r × ~v = Ze L ~ B cr 3 mcr 3 (2.9) ~ = m~r × ~v is the electron orbital angular momentum. The interaction of where L ~ creates a spin-orbit (L ~ · S) ~ term in the this magnetic field with the electron spin S scattering potential and introduces a spin dependent correction to the Rutherford cross section: σ(θ) = σR (θ)[1 + S(θ)P~ · n̂] (2.10) where S(θ) is the asymmetry or Sherman function, P~ is the polarization ~2 (< Sx > , < Sy >, < Sz >), and n̂ is the unit normal to the scattering plane defined by n̂ = ~ki × ~kf |~ki × ~kf | (2.11) Where ~ki and ~kf are the initial and final wave vectors of the electron respectively. The direction n̂ depends on whether scattering to the left or right is being considered. 2.2 SPIN-RESOLVED ANGLE-RESOLVED PHOTOEMISSION SPECTROSCOPY Figure 2.4: Spin-resolved ARPES (Mott polarimetry) experimental setup. (a) Schematic of the spin-resolved ARPES spectrometer COPHEE. Photoelectrons are energy and momentum analyzed using a hemispherical electrostatic analyzer and are alternately deflected at a frequency of 1 Hz into two orthogonally mounted Mott polarimeters. The dual polarimeter system is shown rotated by 90◦ for clarity. (b) The relationship between the sample and Mott coordinate systems. When θ and φ are both zero, the sample coordinates can be transformed into the Mott coordinates via a 45◦ rotation about their common z axis. The Mott axes marked red denote the spin components that the polarimeter is sensitive to. The figure is adapted from Ref. [136]. This spin-orbit scattering relation allows for the measurement of the component of spin polarization perpendicular to the scattering plane in the following way. Consider a beam of N incident electrons with N↑ of them polarized along +z and N↓ of them along -z, which leads to a net polarization Pz = (N↑ − N↓ )/(N↑ + N↓ ). When the scattering of this beam from a nucleus takes place in the xy plane, there results a left-right scattering asymmetry Az (θ) defined as: Az (θ) = NL − NR NL + NR (2.12) where NL and NR are the number of electrons scattered to the left and right respectively through an angle θ. Substituting the relations NL ∝N↑ [1+S(θ)]+N↓ ][1− S(θ)] and NR ∝N↑ [1 − S(θ)] + N↓ ][1 + S(θ)] derived from Equation 5 to Equation 7 38 2.2.2 VLEED yields: Pz = Az (θ) S(θ) (2.13) which shows that given the Sherman function, measurement of Az (θ) yields Pz . In a single Mott polarimeter, it is therefore possible to measure two orthogonal spin components of an electron beam by arranging four detectors in two orthogonal scattering planes in front of a target. 2.2.2 VLEED The concept of VLEED spin detector is based on a simple and intuitive phenomenon, which is that as electrons are injected to a ferromagnetically ordered material, the intensities of diffracted beams in general depend on the spin polarization of the primary electron beam relative to the sample magnetization. Obviously, the efficiency of such detector depends on the ratio of electrons that are being reflected with respect to other processes. In a simplified kinematic picture, the intensity modulation can be described in terms of constructive or destructive interference of reflections from different lattice planes. As the energy of the primary beam is lowered, the radius of the Ewald sphere decreases until it is smaller than the smallest reciprocal lattice vector. In this situation there are no higher-order diffracted beams, and only the specularly reflected beam can be observed. This leads to an increase of the intensity of the specular beam in LEED at very low energies VLEED, which sets one of the foundation for using VLEED as an efficient spin detector. So far in the above-paragraph, the discussion only contains the issue how to enhance the the simple reflection of an electron beam, but it has not covered the spin sensitivity. Let us consider a VLEED process on a ferromagnet, such as an iron (Fe) crystal. In a ferromagnetic material the spin degeneracy of the electronic states is lifted by the exchange interaction, such that, e.g., a critical point in the band 2.2 SPIN-RESOLVED ANGLE-RESOLVED PHOTOEMISSION SPECTROSCOPY structure occurs at lower energy for the majority states than for the minority states. Therefore, the features in the energy dependence of the absorption and reflection probability occur at different energies for majority and minority states. This may be used to realize a spin-dependent scattering for electron spin analysis. Of the three elemental 3d ferromagnets, Fe has the largest exchange splitting of about 2.5 eV. Therefore Fe is a good candidate for this type of spin polarimeter. Figure 2.5: Spin-resolved ARPES (VLEED) experimental setup. Left: Schematic layout of hemispherical energy analyzer with VLEED spin polarimeter. A normal hemispherical electron analyzer (HA 50 are operated by the HAC 300 unit) is first used to detect the energy and the momentum of the electronic states. The spin polarimeter requires three additional voltage supplies EP , lens, and Vsc . The long dashed line shows light incidence, the short dashed line shows an electron trajectory. Channeltron 1 (labeled ch. 1) is for acquiring non spin-resolved data when the scattering target is removed. Channeltron 2 is for counting the electrons scattered back under 10◦ from the magnetized Fe surface. Right: Spin-dependent specular electron scattering off a Fe(100) film at about 10◦ incidence angle. (a) Number of scattered electrons; filled symbols are for parallel magnetization of scattering target and photoemission source, empty symbols for antiparallel magnetization; (b) asymmetry; and (c) figure of merit. The figure is adapted from Ref. [137]. Fig. 2.5 (left panel) shows schematically the layout of the Fe VLEED spin detector. The spectrometer is a commercial hemispherical analyser (HA 50, 50 mm mean radius, with power supply HAC 300 by VSW). Behind the exit slit of the analyzer, the 40 2.2.2 VLEED channeltron was replaced by a three-element electron lens, which transfers the energyanalyzed electrons to a drift chamber. The scattering target is located on the optical axis in the drift chamber. The drift chamber is equipped with coils for magnetizing the Fe target. The coils are made of self-supporting 1 mm Cu wire with four turns of 20 − 25 mm diameter. During data acquisition they are kept at the same potential as the scattering chamber and the target. The right panels of Fig. 2.5 demonstrate the ability of such Fe VLEED detector for measuring spin polarization. Polarized electrons were excited from a magnetized Fe sample by 90 eV photons. Such polarized electrons are injected to the VLEED detector with the magnetization of the Fe target set for one direction. The counts for the scattering at different binding energies are recorded by the empty triangles in the top right panel of Fig. 2.5. Now we flip the magnetization of the Fe target in the VLEED detector, and perform the same measurements, where the counts are recorded by the solid triangles in the top right panel of Fig. 2.5. It can be seen that a clear asymmetry between these two scattering geometries is observed, which demonstrates that the scattering of a polarized electron beam is quite sensitive to the magnetization direction of the VLEED target. Thus the spin polarization of the incidnet electrons can be measured based on this principle. In reality, although Fe (001)/Ag(100) surface has a very high spin dectection efficiency as a VLEED detector, one complication is that the efficiency is strongly dependent on the quality of the Fe (001) surface [137]. And furthermore, the Fe (001)/Ag(100) surface quality is found to degrade quite fast even within a day [137]. Thus one has to re-prepare the surface once per 12 hours which is inconvenient. In reality, the preoxidized Fe(001)-p(1 × 1)-O targets are often used because they are found to be stable for a much longer time than a clean Fe surface, presumably for weeks. For example, the VLEED spin-resolved ARPES endstation at the Hiroshima Synchrotron Radiation Center (Hisor) in Hiroshima University in Japan uses the 2.3 SAMPLE PREPARATION FOR ARPES preoxidized Fe(001)-p(1 × 1)-O targets as the spin detector [138]. 2.3 2.3.1 Sample preparation for ARPES Single crystal bulk samples Figure 2.6: A schematic of the single crystal bulk sample geometry mounted inside the ARPES measurement chamber. The ceramic top post was used to cleave the sample surface in situ, to ensure a clean surface for measurements. For single crystal bulk samples, they are grown by our collaborators including Prof. R. J. Cava’s group in the Department of Chemistry in Princeton University, Prof. F. C. Chou’s group in the Center for Condensed Matter Sciences in National Taiwan University, Prof. Y. Chen’s group in the Physics Department in Purdue University, Prof. S. Jia’s group in the International Center for Quantum Materials, Peking University, Beijing 100871, China. In order to measure them in ARPES, one needs a very clean and flat surface because ARPES is a very surface-sensitive probe. To do so, the sample is then 42 2.3.2 MBE film samples mounted in a geometry as depicted by Fig. 2.6. The crystals are first cut into pieces of approximately 2 mm × 2 mm × 0.5 mm. A small piece is then mounted onto a copper post, using the commercial epoxy resin Torr seal. For other samples with poor electrical conductivity, silver epoxy is used instead to ensure good electrical contact with the sample holder. A ceramic top post is then attached onto the sample with another layer of epoxy. After the sample is mounted inside the ARPES measurement chamber, it is cooled and pumped down for a few hours. The sample was then cleaved insitu at pressures of less than 1 × 10−10 torr, by knocking down the ceramic top-post with a cleaver. The exposed surface was typically visually shiny, indicating a flat surface. 2.3.2 MBE film samples For MBE film samples, they are grown by our collaborators such as Prof. N. Sarmarth’s group in the Department of Physics in The Pennsylvania State University, and Prof. S. Oh’s group in the Department of Physics & Astronomy, The State University of New Jersey. For MBE samples, they are usually too thin (≤ 40 nm) to be cleaved. Let us take the example of thin Bi2 Se3 films grown on some substrates [e.g. GaAs(111)]. In order to protect the surface from oxidation, a thick Se capping layer is deposited on the Bi2 Se3 thin film immediately before taken out of the MBE growth chamber [see Fig. 2.7(a)]. Such a Se capped sample is then loaded into the ARPES chamber and pumped down to high vacuum. In order to reveal the clean Bi2 Se3 surface needed for photoemission measurements, the MBE-grown thin films are heated up inside the ARPES chamber to ∼ 250◦ C to blow off the Se capping layer on top of the Bi2 Se3 film. During the annealing, the pressure goes up and typically remains better than 1 × 10−9 torr. Fig. 2.7(b) demonstrates the decapping process by ARPES core level spectroscopies measurement. Only selenium core level is observed before the 2.3 SAMPLE PREPARATION FOR ARPES Figure 2.7: Demonstration of sample surface preparation (decapping) procedure for the Bi2 Se3 MBE thin films in ARPES measurements. (a) Sample layout of the MBE grown Bi2 Se3 films. (b) Core level spectroscopies on MBE thin film before and after the decapping procedure. (c) typical ARPES dispersion mapping and corresponding energy dispersion curves (EDCs) of Bi2 Se3 thin film along the M̄ − Γ̄ − M̄ momentum-space cut-direction. decapping process (blue curve), whereas both selenium and bismuth peaks are shown after the decapping (red curve). ARPES measurements are then performed on the clean thin film surface. Fig. 2.7(c) shows a typical ARPES measured dispersion mappings after decapping of a Bi2 Se3 thin film, where the sharp ARPES spectrum demonstrates our surface preparation procedure. 44 2.4 Probing the topological number in 3D bulk materials Since the topological number is defined by calculating a global quantity (an integral, a Pfaffian) of the bulk electronic wavefunction over the entire BZ, it is not feasible to measure its value in experiments based on this definition. Rather, the topological number and topological properties are usually probed by studying the boundary of a topological system. Such an approach takes advantage of a fundamental consequence of the topological classification of gapped band structures, which is the existence of gapless conducting states at interfaces where the topological invariant changes. For example, in the case of 2D IQH effect, the quantized transverse conductance provides a measure of the system’s topological number - the Chern number n. How do we probe the topological number in a 3D bulk material? This is particularly an important question to ask in three-dimensions since a 3D bulk topological material is believed to exhibit no quantized transport response. In this section, we use the example of the discovery of the 3D Z2 TI phase in Bi1−x Sbx and Bi2 Se3 classes of materials, to elaborate the way of measuring a 3D topological number by the spinand angle-resolved photoemission spectroscopy (spin-ARPES). For the sake of the simplicity of the presentation, we put the Bi2 Se3 class before Bi1−x Sbx although it was discovered later, because Bi2 Se3 has a simpler surface state that is more suitable for elaborating the methodology. 2.4.1 Separation of insulating bulk from metallic surface states using incident photon energy modulated ARPES In order to probe its topological number states in a 3D Z2 TI via studying its surface states using spin-ARPES, the first thing is to separate the surface states from the bulk bands, which both exist in the electronic structure near the Fermi level. This 2.4 PROBING THE TOPOLOGICAL NUMBER IN 3D BULK MATERIALS is achieved by measuring the electronic dispersion along the out-of-plane kz direction by varying the incident photon energy of the ARPES. We recall that the out-of-plane momentum value is obtained in ARPES by kz = p 1 2m(Ekin cos2 θ + V0 ). We know that Ekin = hν − φ − |EB |. At the Fermi level ~ (EB = 0) and the normal emission kk = θ = 0, we have kz = 1p 2m(hν − φ + V0 ) ~ (2.14) From the equation above, it can be immediately seen that the kz value of the electronic state at the Fermi level and the normal emission is a function of the incident photon energy value hν. Effectively, by varying the incident photon energy value, one can effectively probe the electronic states at different kz values. The topological surface state in 3D TIs is a type of 2D state that are localized on the surface. Therefore, it is expected to be strictly non-dispersive along the kz direction that is perpendicular to the sample surface normal. On the other hand, the bulk conduction/valence bands are (3D) bulk bands. Thus they are expected to show dispersion along all three momentum space directions including kz . Therefore, by measuring the dispersion along the kz direction, one can effectively isolate the topological surface states from the bulk bands. Fig. 2.8 shows an ARPES study on Bi2 Se3 as a function of the incident photon energy. As shown in Fig. 2.8(a). there are three major features in the measured electronic structure: (1) a parabolic intensity continuum at 0≤EB ≤ −0.15 eV; (2) an “X” shaped band that runs from 0 eV to -0.35 eV; (3) an “M” shaped band at higher binding energies (EB ≥ 0.4 eV). As photon energy value is changed, It can be seen that the “X” shaped band shows no change in its dispersion, whereas the a parabolic intensity continuum at the Fermi level and the an “M” shaped band are dispersive. The strong kz dispersion of the bulk valence band at binding energies higher than 46 2.4.2 Surface Dirac crossing, surface-bulk connectivity, and spin-momentum locking Figure 2.8: Topological Surface States and electronic band dispersion along the kz -direction in momentum space. (a) A schematic diagram of the full bulk threedimensional BZ of Bi2 Se3 and the two-dimensional BZ of the projected (111) surface. (b) Electronic dispersion (EB vs kk ) of Bi2 Se3 at different incident photon energies. (c) The energy distribution curves at the Γ̄ (kk = 0) at different photon energies, showing the strong kz dispersion of the bulk valence band at binding energies higher than −0.4 eV. The figure is adapted from Ref. [32]. −0.4 eV is better visualized in Fig. 2.8(c). Therefore, these incident photon energy measurements demonstrate that the “X” shaped Dirac band is a 2D surface state, whereas the other two features originate from the bulk (the bulk conduction and the valence bands). 2.4.2 Surface Dirac crossing, surface-bulk connectivity, and spin-momentum locking Now that we have identified the surface states in Bi2 Se3 , we experimentally show the following properties of the surface states to demonstrate the strong topological insulator state with ν0 = 1 in Bi2 Se3 : • The two branches (left-moving and right moving) of the surface states cross each other, forming a surface Dirac point [Figs. 2.9(c,d)]. • The Dirac surface states span across the bulk energy gap, and connect the bulk conduction and the bulk valence bands [Figs. 2.9(c,d)]. 2.4 PROBING THE TOPOLOGICAL NUMBER IN 3D BULK MATERIALS Figure 2.9: Detection of Z2 (symmetry protected) Topological number in Bi2 Se3 : spin-momentum locking of spin-helical Dirac electrons in Bi2 Se3 and Bi2 Te3 using spin-resolved ARPES. (a) ARPES intensity map at EF of the (111) surface of tuned Bi2−δ Caδ Se3 (see text) and (b) the (111) surface of Bi2 Te3 . Red arrows denote the direction of spin around the Fermi surface. (c) ARPES dispersion of tuned Bi2−δ Caδ Se3 and (d) Bi2 Te3 along the kx cut. The dotted red lines are guides to the eye. (e) Measured y component of spin-polarization along the Γ̄-M̄ direction at EB = −20 meV, which only cuts through the surface states. Inset shows a schematic of the cut direction. (f ) Measured x (red triangles) and z (black circles) components of spin polarization along the Γ̄-M̄ direction at EB = -20 meV. (g) Spin-resolved spectra obtained from the y component spin polarization data. (h) Fitted values of the spin polarization vector P. The figure is adapted from Ref. [34], except Panel (g) which is adapted from Ref. [32]. 48 2.4.2 Surface Dirac crossing, surface-bulk connectivity, and spin-momentum locking • The surface state Fermi surfaces enclose the Kramers points of the surface BZ [Figs. 2.9(a,b)]. • The surface state spin is locked with its momentum [Figs. 2.9(e,f)]. • There are an odd number of such spin-momentum locked surface state Fermi surfaces [Fig. 2.9(g)]. We note that the first two points guarantee that the surface state cannot be adiabatically removed from the bulk band-gap; the third and forth points reveal that the surface states (therefore the topological phase) are protected by the time-reversal symmetry; the last point shows that Bi2 Se3 is a strong not a weak TI. Similarly, we can use ARPES and spin-ARPES to probe the Z2 topological state in Bi0.91 Sb0.09 . • The two branches (left-moving and right moving) of the surface states cross each other, forming a surface Dirac point [Figs. 2.10(c,f)]. Now there are surface band crossings both at the Γ̄ and the M̄ Kramers points. • The Dirac surface states span across the bulk energy gap, and connect the bulk conduction and the bulk valence bands [Figs. 2.10(c,f)]. • The surface state Fermi surfaces enclose the Kramers points of the surface BZ [Fig. 2.10(d)]. • The surface state spin is locked with its momentum [Fig. 2.10(g)]. • There are an odd number of such spin-momentum locked surface state Fermi surfaces [Fig. 2.10(d)]. We put Bi0.91 Sb0.09 after Bi2 Se3 , even though the experiments on Bi0.91 Sb0.09 were earlier than Bi2 Se3 , because the topological surface states in Bi0.91 Sb0.09 is relatively more complicated. There are multiple (5) pieces of surface state Fermi surface 2.4 PROBING THE TOPOLOGICAL NUMBER IN 3D BULK MATERIALS Figure 2.10: Spin texture of the topological surface states in Bi0.91 Sb0.09 encodes its Z2 topological number of the bulk (2008). (a) Schematic sketches of the bulk Brillouin zone (BZ) and (111) surface BZ of the Bi1−x Sbx crystal series. (b) Schematic of Fermi surface pockets formed by the surface states (SS) of a topological insulator that carries a Berry’s phase. (c) Partner switching band structure topology. (d) Spin-integrated ARPES intensity map of the SS of Bi0.91 Sb0.09 at EF . Arrows point in the measured direction of the spin. (e) High-resolution ARPES intensity map of the SS at EF that enclose the M̄1 and M̄2 points. Corresponding band dispersion (second derivative images) are shown below. The left right asymmetry of the band dispersions are due to the slight offset of the alignment from the Γ̄-M̄1 (M̄2 ) direction. (f ) Surface band dispersion image along the Γ̄-M̄ direction showing five Fermi level crossings. (g) Spin-resolved momentum distribution curves presented at EB = −25 meV showing single spin degeneracy of bands at 1, 2 and 3. Spin up and down correspond to spin pointing along the +ŷ and -ŷ direction respectively. (h) Schematic of the spin-polarized surface FS observed in our experiments. This figure is adapted from Ref. [31]. 50 2.4.2 Surface Dirac crossing, surface-bulk connectivity, and spin-momentum locking [Fig. 2.10(d)]. The surface states connect the bulk conduction and valence bands in a more complicated path [Figs. 2.10(c,f)]. The dispersion of surface states are bent away from the surface band crossing. Therefore, the description of a Dirac crossing is only valid at a very small k−space in the close vicinity of the Kramers points. However, despite all these complicities, it can be seen that by measuring the electronic and spin groundstate of the surface electrons, the Z2 topological number (ν0 = 1) can be experimentally demonstrated in Bi0.91 Sb0.09 . The above methodology (using spin-ARPES to electronic and spin groundstate for the surface states of a bulk material) can be more generally applied to detect the other topological number in a bulk material, and therefore to discover new topological phases of matter. In general, there are two important logic steps: (1) To show that the surface states have band crossings and they connect across the bulk band-gap from the conduction to the valence bands. This basically demonstrates the topological nontriviality of the surface states, because such kind of surface states cannot be removed from the band gap unless one closes the bulk band-gap (requires a band inversion) or opens up a gap at the surface band crossing (requires breaking a symmetry). (2) To study the spin polarization texture as well as the Fermi surface of the surface states. This reveals the symmetry that protects the topological phase and its surface states are protected and also provides an experimental measure of the associated topological number. Chapter 3 Topological Quantum Phase Transition in BiTl(S1−δ Seδ )2 A topological material is a distinct phase of matter since it features a nonzero topological number in the bulk electronic structure groundstate that can only be removed by a topological quantum phase transition into a trivial phase. The topological number guarantees the existence of protected surface states, which serve as the experimental signature for the nontrivial topology. In this chapter, we present our experimental realization of a topological quantum phase transition (TQPT) from a conventional band insulator to a 3D Z2 topological insulator in the BiTl(S1−δ Seδ )2 system. We systematically study the evolution of surface and bulk electronic and spin groundstate across the topological phase transition. This study provides a general paradigm for understanding how various topological phases and their protected surface states arise from a conventional material in experiments, and is of value for searching for new and engineered topological states in real materials. Our study is further suggestive for realizing many fascinating physics such as higher dimensional Dirac fermions [120, 139], Weyl fermions under magnetization [119, 120, 139–141], supersymmetry SUSY state [128] and interacting topological states [142] predicted in the vicinity of the critical point 52 of a topological quantum phase transition. 3.1 Evolution of the electronic groudstate across a topological quantum phase transition As we have discussed above, if the system changes from a conventional band insulator to a 3D Z2 topological insulator, it must go through a band inversion process. The basic evolution of the bulk electronic structure across a topological quantum phase transition from a conventional band insulator to a 3D Z2 TI have been theoretically discussed in Ref. [120]. Here we state the conclusions in Ref. [120] without going into the details of the formulations. Figure 3.1: Phase transition in 3D between the conventional band insulator to the 3D Z2 TI phases for inversion-symmetric and inversion-asymmetric cases. In the inversion symmetric case, all bands are doubly degenerate. Since time-reversal symmetry is indispensable for a Z2 TI phase, thus here we restrict ourselves on time-reversal-symmetric systems. Besides time-reversal symmetry, another symmetry that plays an essential role is the space inversion symmetry. This THE ELECTRONIC GROUDSTATE ACROSS A TOPOLOGICAL QUANTUM PHASE TRANSITION Figure 3.2: Bulk band-gap across the topological phase transition in 3D between the conventional band insulator to the 3D Z2 TI phases for inversion-symmetric and inversionasymmetric cases. is because inversion symmetry can force the bulk bands to be doubly degenerate at all k-points throughout the BZ, whereas for systems without inversion symmetry, their bulk bands can be singly degenerate at all k-points except the Kramers point (doubly degeneracy forced by the Kramers theorem). We will discuss the band inversion process for inversion symmetric and asymmetric cases separately. Finally, we note that we do not consider any additional space group symmetries (such as mirror symmetries or rotational Cn symmetries). In the case of the presence of these additional symmetries, then the conclusion can be different again. For example, please refer to the topological Dirac semimetal phase discussed in Chapter 5. Suppose we start from a conventional band insulator in 3D, and there exists some tuning parameter δ (e.g. spin-orbit coupling, lattice constant, chemical composition, temperature, etc.) that can effectively change the bulk band-gap. For an inversion symmetric case, the conclusion is shown in Figs. 3.1, 3.2: (0) In an inversion symmetric crystal, all bulk bands must remain doubly degenerate at all kpoints. (1) As the system goes through the band inversion, its band-gap decreases to zero and then increases again. (2) There exists only a single value for the δ, where the band-gap is zero. This is the critical point of the band inversion and the topological phase transition. At this critical point, the bulk conduction and valence bands cross, and the bulk band structure can be described by a 3D massless Dirac cone. (3) The 54 bulk band crossing (the 3D Dirac point) must occur at a Kramers point. For an inversion asymmetric case, the conclusion is shown in Figs. 3.1, 3.2: (0) In an inversion asymmetric crystal, bulk bands (with consideration of the spin-orbit coupling) are usually singly degnerate except at the Kramers points. (1) As the system goes through the band inversion, its band-gap decreases to zero and then increases again. (2) There exists a range of δ values for the where the band-gap is zero. Thus the gapless phase is not a single point by a region along the δ axis. The gapless region is called the Weyl semimetal phase, because the low energy excitation from the bulk bands are described by the Weyl equation. This is called a Weyl semietal phase because one can actually identify a distinct topological number to it, and therefore it is a new topological phase of matter. (3) The bulk band crossings (the 3D Weyl points) will not occur at any Kramers points. The Weyl semimetal phase in inversion asymmetric systems are of great current interest, which remains experimentally elusive, and many groups are trying to realize it. On the other hand, in the following sections in this chapter, we only consider systems with inversion symmetry because it is directly relevant to our experiments (BiTl(S1−δ Seδ )2 has inversion symmetry). In the next section, we present the experimental work that demonstrates the general frame of the band inversion and the topological phase transition in BiTl(S1−δ Seδ )2 . Then in the following section, we focus on the vicinity of the critical point of the topological phase transition, and try to reveal the formation mechanism of the topological surface states (how protected surface states arise from a conventional material) by going through a topologicalcritical-point. 3.2 TOPOLOGICAL QUANTUM PHASE TRANSITION IN BITL(S1−δ SEδ )2 3.2 3.2.1 Topological quantum phase transition in BiTl(S1−δ Seδ )2 Identifying a suitable topological material system A 3D Z2 topological insulator is a distinct phase of matter that cannot be adiabatically deformed into a conventional band insulator in a time-reversal invariant condition without going through a topological quantum phase transition. Within band theory, the evolution of the bulk electronic groundstate across the topological phase transition is effectively described the band inversion process. Therefore, realizing and studying a band inversion and a topological quantum phase transition in real materials is of critical importance for understanding the 3D Z2 topological insulator phase, and in general how nontrivial topological phases arise from a conventional band insulator. In order to realize a band inversion and a topological quantum phase transition in experiments, there are two critical conditions: (1) one has to identify a real material system, where there exists a material parameter δ that can effectively tune the bulk band-gap and the topological nature of the system, and (2) there has to be an appropriate experimental probe, which can reveal the evolution of the electronic groundstate across the topological transition at all δ values. While point (2) is solved by the utilization of the spin-ARPES to measure the protected surface states and their spin texture in bulk topological materials, point (1) had remained experimentally unachieved for quite a long time. For example, Bi0.91 Sb0.09 is the first 3D topological insulator realized in experiments [30]. It has a single band inversion at the T point of the bulk BZ. However, Bi1−δ Sbδ is not suitable for realizing a topological phase transition for several reasons: (1) By going from Bi0.91 Sb0.09 to pure Sb (0.09 ≤ δ ≤ 1), the topological nature of the system is unchanged. There remains only one band inversion at the T point, and thus the system remains Z2 topologically nontrivial ν0 = 1. The only change is that the energy position of the H band shifts up, see Fig. 3.3. Thus while Bi0.91 Sb0.09 is an 56 3.2.1 Identifying a suitable topological material system Figure 3.3: (a) Bulk 3D Brillouin zone of Bi1−δ Sbδ showing the eight bulk Kramers points (T , Γ, 3 L, 3 X). (b) Schematic evolution of the near EF band structure from Bi to Sb. This figure is adapted from Ref. [136] insulator, pure Sb is a metal. (2) By going from Bi0.91 Sb0.09 to pure Bi (0.09 ≥ δ0), the topological nature is indeed changed, because it induces another three band inversions at the three L points of the bulk BZ [see Fig. 3.3(a)]. Thus Bi0.91 Sb0.09 is Z2 topologically nontrivial ν0 = 1, whereas pure Bi is Z2 topologically trivial ν0 = 0. However, the reality is much more complex. Since there do exist four band inversions at the 1T and 3L points in pure Bi, and furthermore these band inversions coincide with the mirror planes of the Bi crystal, therefore pure Bi does have surface states within its partial energy gap (energy gap at each k point) and these surface states can be protected by the mirror symmetries [117] (although pure Bi is Z2 topologically trivial). Moreover, pure Bi is also a metal lacking a global energy gap. Furthermore, the Bi0.91 Sb0.09 (ν0 = 1) is known to have multiple pieces of surface state Fermi surfaces (both at the Γ̄ and the M̄ points), but so is pure Bi (ν0 = 0). These facts suggest that the Bi1−δ Sbδ is quite complicated both in terms of its evolution of the topology and in terms of its surface state electronic structure as a function of δ. Thus it is difficult to demonstrate a prototypic topological phase transition in the Bi1−δ Sbδ system. Another important topological insulator material is Bi2 Se3 discovered in 2009 [32, 33]. It has a layered rhombohedral structure with the space group of R − 3m. In Ref. [33], Zhang et al. further predicted that Sb2 Se3 is topologically trivial. Thus it seems 3.2 TOPOLOGICAL QUANTUM PHASE TRANSITION IN BITL(S1−δ SEδ )2 like (Bi1−δ Sbδ )2 Se3 is a promising system for a topological phase transition. However, it is important to note that Sb2 Se3 in fact crystalizes in a very different crystal structure (an orthorhombic structure with the space group of P nma) [143]. Thus by going from Bi2 Se3 to Sb2 Se3 , the system will go through a structural transition, where the electronic structure is dramatically changed. Therefore, the (Bi1−δ Sbδ )2 Se3 system is also not ideal for the realization of a prototypic topological phase transition. 3.2.2 Topological quantum phase transition in BiTl(S1−δ Seδ )2 Figure 3.4: (a) Bulk 3D Brillouin zone of BiTl(S1−δ Seδ )2 showing the eight bulk Kramers points (T , Γ, 3 L, 3 X), and their (111) surface projections. (b) Fermi surface map over the entire first surface BZ of the (111) surface of BiTlSe2 (δ = 1). Only a single surface state Fermi surface at the Γ̄ point is observed. (c) ARPES dispersion maps of the single Dirac cone surface state at the Γ̄ point at three different incident photon energies. Our interest on the BiTl(S1−δ Seδ )2 system starts from its selenium end compound. BiTlSe2 (δ = 1) was identified as a 3D Z2 TI with a single Dirac cone surface state at the surface BZ center Γ̄ point [144–148], which is very similar to Bi2 Se3 . However, interestingly, we found that unlike in Bi2 Se3 where the crystal structure changes by going from Bi2 Se3 to Bi2 S3 or Sb2 Se3 , the BiTl(S1−δ Seδ )2 system remains the same crystal structure (Fig. 3.5) throughout the compositional range going from BiTl(S1 Se0 )2 to BiTl(S0 Se1 )2 . Thus by going from the sulfur end to the selenium end, the two major changes are the change of the lattice constant [Fig. 3.5(b)] and the strength of spin-orbit coupling (since Se is heavier than S). Both changes are adiabatic, leading 58 3.2.2 Topological quantum phase transition in BiTl(S1−δ Seδ )2 Figure 3.5: (a) The crystal structure of the BiTl(S1−δ Seδ )2 system. (b) In-plane lattice constant a and out-of-plane lattice constant c determined by x-ray diffraction measurements. The crystal structure remains the same, only the lattice constant value is found to change as a function of the composition δ. to an adiabatic evolution of the bulk electronic groundstate. These facts inspires us to systematically study the BiTl(S1−δ Seδ )2 system as a function of chemical composition in order to search for the experimental realization of a topological phase transition. Fig. 3.6(a) presents systematic photoemission measurements of surface and bulk electronic states that lie between a pair of time-reversal invariant points or Kramers points (Γ̄ and M̄ ) obtained for a series of compositions δ of the spin-orbit material BiTl(S1−δ Seδ )2 . As the selenium concentration is increased, the low-lying bands separated by a gap of energy 0.15 eV at δ = 0.0 are observed to approach each other and the gap decreases to less than 0.05 eV at δ = 0.4. The absence of surface states (SSs) within the bulk gap demonstrates that the compound is topologically trivial for composition range of δ = 0.0 to δ = 0.4. Starting from δ = 0.4, a linearly dispersive band connecting the bulk conduction and valence bands emerges which threads across 3.2 TOPOLOGICAL QUANTUM PHASE TRANSITION IN BITL(S1−δ SEδ )2 the bulk band gap. Moreover, the Dirac-like bands at δ = 0.6. The system enters a topologically non-trivial phase upon the occurrence of an electronic transition between δ = 0.4 and δ = 0.6. While the system approaches the transition from the conventional side (δ = 0.6), both energy dispersion and FS mapping (Fig. 3.6(a) for δ = 0.4) show that the spectral weight at the outer boundary of the bulk conduction band continuum which corresponds to the loci where the Dirac SSs would eventually develop becomes much more intense; however, that the surface remains gapped at δ = 0.4 suggests that the material is still on the trivial side. A critical signature of a topological transition is that the material turns into an indirect bulk band gap material. As δ varies from 0.0 to 1.0 [Fig. 3.6(c)], the dispersion of the valence band evolves from a “Λ”-shape to an “M”-shape with a “dip” at the Γ̄ point (k = 0); the δ = 0.0 compound features a direct band gap in its bulk, whereas the δ = 1.0 indicates a slightly indirect gap. These systematic studies demonstrate the existence of the bulk band inversion and the topological phase transition between a conventional band insulator and a Z2 topological insulator in the BiTl(S1−δ Seδ )2 system. This is the first experimental realization of a topological phase transition in a tunable band insulator system, where the evolution of the surface and bulk electronic groundstate can be systematically tuned and visualized [37]. In order to reveal the band inversion process responsible for the topological transition, we track the energy positions of the bulk conduction band minimum and the valence band maximum at various compositions. As shown in Fig. 3.7, an inversion + between the bulk conduction and valence bands (the Γ− 4 and Γ4 bands) is clearly vi- sualized. Using linear interpolation, we estimate the critical point of this topological phase transition to be at composition value δc = 0.5 ± 0.05. In the next section, we will systematically study the surface electronic and spin groundstate near the critical point with finer compositional steps. Nevertheless, the work presented in Figs. 3.6, 3.7 sets the foundation for the realization of the topological quantum phase transition in 60 3.2.2 Topological quantum phase transition in BiTl(S1−δ Seδ )2 BiTl(S1−δ Seδ )2 . 3.2 TOPOLOGICAL QUANTUM PHASE TRANSITION IN BITL(S1−δ SEδ )2 Figure 3.6: Topological quantum phase transition in BiTl(S1−δ Seδ )2 . (a) Highresolution ARPES dispersion maps along the Γ̄ − M̄ momentum space line, from a conventional band insulator (left panel) to a topological insulator (right panel). Band insulators and topological insulators are characterized by a different Z2 topological number ν0 = 0, and ν0 = 1, respectively. (b) ARPES Fermi surface maps at different compositional values. (c) Left and right panels: Energy-distribution curves for stoichiometric compositions δ = 0 and δ = 1, respectively. Center panels: ARPES spectra indicating the bulk band-gap and Dirac node for compositions δ = 0.2 to δ = 0.8. (c) Evolution of surface and bulk electronic ground state imaged over as a function of energy (vertical axis), spin (arrows), and in-plane momentum kx , ky (horizontal plane). Spin textures are indicated by yellow arrows above the Dirac node and green arrows below the Dirac node. Each arrow represents the net polarization direction on a k-space point on the corresponding Fermi surface. The figure is adapted from Ref. [37]. 62 3.2.2 Topological quantum phase transition in BiTl(S1−δ Seδ )2 Figure 3.7: Bulk band inversion process in BiTl(S1−δ Seδ )2 . A band inversion is revealed by tracking the ARPES measured energy positions of the conduction band minimum and valence band maximum at various composition δ values. The figure is adapted from Ref. [37]. 3.2 TOPOLOGICAL QUANTUM PHASE TRANSITION IN BITL(S1−δ SEδ )2 3.2.3 Spin-orbit coupling vs. lattice constant Figure 3.8: Comparing the role of spin-orbit coupling and lattice constant in the topological phase transition in BiTl(S1−δ Seδ )2 . (a) Bulk band structure calculation of BiTl(S0 Se1 )2 and BiTl(S1 Se0 )2 . Top row: Calculated Band structure will full SOC. Bottom row: Calculated Band structure with S or Se SOC setting to zero. Black (parity −) and red (parity +) represent orbital symmetries associated with the parity eigenvalue at the high symmetry points. (b) Lattice constant change as a function of composition. We try to determine what is the pivotal tuning parameter that drives the topological phase transition in BiTl(S1−δ Seδ )2 . As we have discussed above, as the composition δ is varied, the two major changes in the system are the spin-orbit coupling strength (since Se is heavier than S) and the lattice constant. Here we evaluate which one plays the decisive role in this topological transition. Fig. 3.8(a) shows the bulk band structure calculation with the parity eigenvalues ± of the lowest conduction and valence bands. Let us first focus on the top row of Fig. 3.8(a), which are calculations with full spin-orbit coupling strength. It can be seen from Fig. 3.8(a) that the Se end compound BiTl(S0 Se1 )2 (δ = 1) shows a parity inversion, consistent with a nontrivial TI phase, whereas the S end compound BiTl(S1 Se0 )2 (δ = 0) does not show parity inversion, consistent with a topologically trivial phase. Now, in the bottom 64 3.2.3 Spin-orbit coupling vs. lattice constant row of Fig. 3.8(a), we turn of the spin-orbit coupling in S and Se, only the spin-orbit coupling of the Bi and Tl atoms are considered. However, as seen in the bottom row of Fig. 3.8(a), the results remain the same. Therefore, these calculation results demonstrate that the increase of spin-orbit coupling from S to Se does not play a major role in the topological phase transition in BiTl(S1−δ Seδ )2 . The lattice constant change, on the other hand, is more decisive. 3.2 TOPOLOGICAL QUANTUM PHASE TRANSITION IN BITL(S1−δ SEδ )2 3.2.4 3D Dirac semimetal state at the critical point Figure 3.9: 3D Dirac semimetal state at the critical point of the topological phase transition in BiTl(S1−δ Seδ )2 . (a) Theoretically calculated band inversion and topological phase transition in the BiTl(S1−δ Seδ )2 system. Inset: a 3D Dirac semimetal state at the critical point of this phase transition is seen in calculated bulk band structure (b) ARPES results at the composition δ = 0.5, which corresponds to the critical point. We also note that a 3D Dirac semimetal state is realized at the critical point of the topological phase transition in BiTl(S1−δ Seδ )2 . This has been discussed in the first section of this chapter (see section 3.1). Since BiTl(S1−δ Seδ )2 has inversion symmetric, according to the discussion in section 3.1, the bulk band-gap goes to 0 at only one value of the tuning parameter δ, which corresponds to the critical point of this topological phase transition. At the critical point, the bulk band structure is exptected to be described by a 3D Dirac fermion state, where the band disperses 66 3.2.4 3D Dirac semimetal state at the critical point linearly along all three momentum space directions. This is indeed seen in our theoretical calculation shown in Fig. 3.9(a). Furthermore, our ARPES measurements of the critical composition δ = 0.5 also show a spectrum consistent with a 3D Dirac cone [Fig. 3.9(a)]. But as we will systematically discuss in the next section, the real situation is richer. While the bulk band structure is indeed described by a 3D Dirac cone, the surface electronic ground state show exotic “preformed” behavior (see next section). 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES 3.3 Topological-critical-point and the “preformed” surface states After establishing the topological phase transition and band inversion in the BiTl(S1−δ Seδ )2 , in this section we systematically study the electronic and spin groundstate of the BiTl(S1−δ Seδ )2 near the critical point of the topological transition. Studying the topological-critical-point of a topological phase transition is of fundamental importance for the following reasons: Understanding the physics of distinct phases of matter is one of the most important goals in physics in general. For a new phase of matter, a powerful route toward such understanding is to study the way it arises from an understood state by investigating the nature of a phase transition. Studying the phase transition critical point not only deepens our understanding of the new phase, but also sometimes even produces surprising new phenomena. A well-known example is the study of the superconducting phase transition between the high-Tc d−wave cuprate superconductor and the normal state, which leads to the surprise of the pseudo-gap state with the concept of the “preformed” Cooper pairing. In our context, a topological insulator is a distinct phase of matter that cannot be adiabatically connected to a conventional material without going through a topological quantum (T → 0 K) phase transition (TQPT), which involves a change of the bulk topological invariant. Inspired by the discovery of 3D Z2 topological insulator state [2–9,11–13], many new topological phases of matter, such as a topological crystalline insulator [39–41], a topological Kondo insulator [49–52, 118], a topological Dirac/Weyl semimetal [43–45,119,120,139], etc, have just been predicted or realized. All these phases are predicted to feature protected surface states, which serve as the experimental signature for their nontrivial topology in the bulk, and they are in fact formed via TQPTs and need to be understood in real materials. Therefore, it is of general importance to study how protected surface state emerge from a trivial 68 material by crossing the topological-critical-point (TCP) of a TQPT. As an example, for a Z2 topological insulator, it is well established that the odd number of Dirac surface states and their spin-momentum locking are the signature that distinguishes it from a conventional insulator. However, an interesting and vital question that remains unanswered is how topological surface states emerge as a non-topological system approaches and crosses the TCP. One might imagine that there are neither surface states nor spin polarization in the conventional insulator (non-topological) regime. In this case, the gapless topological surface states and spin-momentum locking set in abruptly and concomitantly at the topological-criticalpoint. However, here in this section, we report observation of an exotic, unexpected , and yet intuitive phenomenon that there exists a form of novel precursor to the topological surface states in the non-topological regime, and the spin-locking is nonconcomitant. Thus they go through a “preformed” state. These preformed surface states are systematically enhanced and evolve into the actual topological surface states across the TCP. This is particularly interesting because it can be viewed as a novel “proximity effect” (in material compositional space) due to the adjacent topological insulator phase. Therefore, in order to understand the formation of protected surface states in a Z2 TI, and also to establish a general guideline for such formation in various topological phases, one needs to critically study the electronic and spin groundstate in the close vicinity of the TCP of a TQPT, with spin and momentm resolution, in a real topological material. Understanding the nature of a TCP is also of broad interest because recent theories have proposed a wide range of exciting quantum phenomena based on topological criticality. It has been proposed that the TCP of various TQPTs can not only realize new groundstates such as higher dimensional Dirac fermions [120,139], Weyl fermions under magnetization [120,139–141], supersymmetry SUSY state [128] and interacting topological states [142], but also show exotic transport and optical responses such 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES as chiral anomaly in magnetoresistence [149] or the light-induced Floquet topological insulator state [150]. Realization of these very recent theoretical proposals can truly open a new era in fundamental topological physics [128, 142]. In order to achieve them in real materials, it is also quite suggestive to study the electronic and spin groundstate in the vicinity of the TCP in some great detail. In this section, in order to illuminate the nature of a topological-critical-point, we systematically study the evolution of electronic and spin groundstate near the topological-critical-point with a step finer than 2% in the prototype TQPT BiTl(S1−δ Seδ )2 system. The BiTl(S1−δ Seδ )2 system is known to host one of the most basic TQPTs between a conventional band insulator and a 3D Z2 topological insulator (TI) [37,38,75], and is therefore an ideal platform for our goal. We present in-plane electronic structure (EB vs kk ) of the BiTl(S1−δ Seδ )2 system at varying compositions (δ). Fig. 3.10 shows that the two end compounds (δ = 0.0 and 1.0) are in clear contrast, namely, δ = 0.0 has no surface states and δ = 1.0 has surface states connecting the bulk conduction and valence bands, which clearly reveals the difference between the conventional semiconductor phase and the Z2 topological band insulator phase, in agreement with previous studies [37, 38]. The conventional semiconductor state is found to extend from δ = 0.0 to 0.4 [Fig. 3.10(a)], whereas the topological state is clearly observed from δ = 1.0 to 0.6 [Fig. 3.10(c)]. A small but observable bulk band-gap of about 30 meV is observed for δ = 0.45 in Fig. 3.10(e), indicating that the system continues to belong to the conventional semiconductor phase. Upon increasing δ to the region of 0.475 − 0.525, the bands are found to further approach each other, and the linear dispersion behavior of the bands is observed to persist at energies all the way across the node (the Dirac point). Thus based on the observed linear dispersion, the critical composition can be estimated to be δc = 0.5 ± 0.03. At δ = 0.60 [Fig. 3.10(c)], a clear bulk conduction band is observed inside the surface states’ upper Dirac cone. Moreover, the bulk conduction 70 and valence bands are separated by an observable bulk gap, which is traversed by the gapless topological surface states. Thus, our data show that the system belongs to the topological insulator regime for compositions of δ ≥ 0.60. As for the system lying very close to the bulk inversion at δ = 0.50 or 0.525, based on the in-plane dispersion data in Fig. 3.10(b) alone, the nature of the observed Dirac-like band cannot be conclusively determined, because it can be interpreted as two-dimensional topological surface states or three-dimensional bulk Dirac states [139] expected near the bulk band inversion. However, one of the two possibilities can be identified by measuring the dispersion along the out-of-plane kz direction, since the three-dimensional bulk Dirac states are expected to be highly dispersive [37, 43, 45] (the velocity along kz −1 direction of the 3D bulk Dirac band at δc is estimated to be ∼ 2.5 eV·Å [37]), whereas the 2D surface states are not expected to show observable dispersion along the kz direction. Thus, in order to better understand the nature of the bands at compositions near the TCP, we perform ARPES measurements as a function of incident photon energy values [Fig. 3.10(e),(f) to probe their out-of-plane kz dispersion. Upon varying the photon energy, one can effectively probe the electronic structure at different outof-plane momentum kz values in a three-dimensional Brillouin zone. Left panel of Fig. 3.10(f) shows the incident photon energy (kz ) measurements at δ = 0.525 by the Fermi surface mapping in kk vs kz momentum space. The straight Fermi lines that run parallel to the kz axis show nearly absence of observable kz dispersion. Similarly, incident photon energy measurements are also performed at compositions δ = 0.40 and 0.45, where a clear bulk band-gap is observed (ν0 = 0). Surprisingly, even for the gapped electronic structure at δ = 0.40, 0.45, our data show clear absence of kz dispersion. Therefore the observed bands cannot be interpreted as three-dimensional bulk Dirac bands expected near the bulk band inversion. In fact, Our systematic kz measurements [(Figs. 3.10(g),(h)]reveal that the electronic structure at δ = 0.40, 0.45 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES is largely dominated by the presence of gapped quasi-2D electronic states, which are found to roughly disperse along the outer boundary of the bulk continuum. Such anomalously strong quasi-2D states that dominate the low energy surface spectral weight suggest a possible preformed nature as a result of their proximity to the topological insulator regime. In order to study the spin properties of the observed anomalous quasi-2D states, we perform spin-resolved measurements on the system with compositions below and near the TCP. We present spin-resolved data taken on the composition of δ = 0.40 [Fig. 3.11(a)] and focus on the vicinity of the Fermi level (EB = −0.02 eV). The momentum distribution curves (MDCs) for the spectrum are shown in Fig. 3.11(b), where the highlighted curve is chosen for spin-resolved (SR) measurements. Fig. 3.11(d) shows the in-plane SR-MDC spectra as well as the measured in-plane spin polarization along the Γ̄-M̄ and Γ̄-K̄ momentum space cuts. Clear in-plane spin polarization is observed on the quasi-2D states from Fig. 3.11(d). Furthermore, the measured spin polarization in Fig. 3.11(d) shows that the spin texture is arranged in a way that spins have opposite directions on the opposite sides of the Fermi surface. In addition, the out-of-plane component of the spin polarization along the Γ̄-M̄ and Γ̄-K̄ cuts is shown in Fig. 3.11(e). No significant out-of-plane spin polarization [Fig. 3.11(e)] is observed within our experimental resolution. The spin texture configuration can be obtained from the spin-resolved measurements in Figs. 3.11(d),(e), as schematically shown by the arrows in Fig. 3.11(c). Surprisingly, our spin-resolved measurements reveal that these quasi-2D states are not only strongly spin-polarized, but their spin texture near the native Fermi level resembles the helical spin texture on the topological surface states as observed in Bi2 Se3 [34]. We present systematic spin-resolved studies to understand the way spin texture of the quasi-2D states evolves as a function of binding energy EB and composition δ. Figs. 3.12(a)-(d) show spin-resolved data at different binding energies for a sample 72 with δ = 0.40. The spin-momentum locking behavior is observed at all binding energies from near the Fermi level (EB = −0.02 eV) to an energy near the conduction band minimum (EB = −0.32 eV). While the magnitude of the spin polarization on the Fermi level is found to be around 0.3, the spin polarization magnitude is found to decrease to nearly zero while approaching small values of momenta near the Kramers’ point Γ̄ (the conduction band minimum). Furthermore, at energies cutting across the bulk valence band at EB = −0.57 eV, EB = −0.72 eV, the measured spin polarization profile is clearly reversed, where a right-handed profile is found for the quasi-2D states on the boundary. In addition, the magnitude of the spin polarization is found to be increased as the energy is tuned away from the bulk band-gap, which is consistent with the gapped nature of the quasi-2D states. The observed reduction of net spin polarization at small momenta and the absence of net spin polarization at the Γ̄ point are important for the gapped nature of quasi-2D states in δ = 0.4 samples. As for the gapless case with the system composition at δ = 0.50, the spin-resolved measurements [Figs. 3.12(e)-(h)] reveal the same helical-like spin texture configuration on the Fermi level, where the magnitude of the spin polarization is around 0.5 at the Fermi level in this composition. However, in contrast to the δ = 0.4 case, it does not show any obvious reduction in going to small values of momenta near the Kramers’ point Γ̄ (spin polarization ∼ 0.45 for EB = −0.32 eV), which is consistent with its gapless nature. The adequate energy-momentum resolution of our SR-ARPES instrument in order −1 to resolve opposite spins at small momenta, such as k ∼ 0.05 Å , is demonstrated by these SR measurements on δ = 0.50, which strongly supports that the observed strong spin polarization reduction at the δ = 0.40 case reveals an intrinsic property of the system relevant to the topological transition. Finally, we present the spin data taken on the composition far into the topologically trivial side (δ = 0.0). Our spinresolved measurements [Figs. 3.12(i)-(l)] show only very weak polarizations (∼0.05), which lie within the uncertainty levels of the measurements. The magnitude of the 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES spin polarization is too weak (comparable to the instrumental resolution) to obtain the spin texture configuration around the Fermi surface for samples with δ = 0.0. The observed weak polarization on δ = 0.0 suggests that the quasi-2D states are much suppressed in going away from the TCP (such as the δ = 0.0 samples). We model the semi-infinite system based on the 4×4 k·p model [151] and utilize the Green’s function method to obtain the spectral weight as well as the spin polarization near the surface region of the system as a function of bulk band-gap value in the model (see details in Supplementary Methods). Indeed, our calculation shows that, in the conventional semiconductor regime prior to the topological transition, the spectral weight near the surface [left two panels of Fig. 3.13] is dominated by a single quasi2D band along the edge of the bulk band continuum, consistent with our ARPES results. Moreover, the calculated spin polarization in the conventional semiconductor region [left two panels of Fig. 3.13(b)] is found to be locked with momentum, also consistent with our spin-resolved measurements. Furthermore, both the calculated spectral weight and the spin polarization is found to become increasingly stronger and predominate upon approaching the TCP from the conventional semiconductor regime. A reasonable qualitative agreement between our experimental results and the k · p model calculation is evident as seen in Fig. 3.13. The physical interpretation of the observed agreement is discussed in the next section. Although the observed quasi-2D states share important properties with actual topological surface states, the following observations from our data clearly show that they are still consistent with the non-topological bulk regime: (i) The experimentally observed quasi-2D states are gapped, and disperse roughly along the edge of the bulk continuum. Thus they do not connect or thread states across the bulk band-gap as in a Z2 topological insulator. (ii) It is also possible to choose an energy value within the bulk band-gap for samples lying in the conventional semiconductor regime (e.g. δ = 0.4), so that no surface state is traversed, consistent with the topological triviality 74 of the sample. These experimental facts guarantee that the observed quasi-2D states at δ . 0.5 are consistent with the conventional semiconductor phase of the system (ν0 = 0, trivial Z2 index). In order to better understand the spin texture of the quasi-2D states, we propose a phenomenological picture consistent with the basic topological physics for our observation (Fig. 3.14): The quasi-2D states can be viewed as a Rashba-like state, whose inner band is not observable because it is severely damped due to its strong overlap with the bulk bands in E − k. As the system is tuned approaching the TCP from the trivial side, the inner band completely loses its surface character, whereas the outer band is systematically enhanced in terms of its surface spectral weight and spin polarization, and evolve into the topological surface states (as clearly observed in our data). We emphasize that we use the term “Rashba-like” for the observed perform surface states because there are two singly degenerate bands as in a real Rashba 2DEG. However, the Rashba surface states are due to a combined effect of atomic spin-orbit coupling and the electrical field perpendicular to the surface, and follows the Rashba Hamiltonian, whereas it is not fully applicable for the observed preformed surface states. This issue needs further theoretical studies to illuminate the microscopic origin of the preformed surface states in theory. Regardless of this issue, our systematic data, which is the main theme of this experimental paper, show: (1) these preformed surface states show spin polarization texture that resembles a topological insulator; (2) their surface spectral weight and magnitude of spin polarization are enhanced as we approach the TCP; (3) they evolve into the topological surface states. These measurements with spin and mometum resolution clearly show that these preformed surface states are critically relevant to the bulk band inversion and TQPT in the bulk. In the Supplementary Figure 8, we show our observation of preformed surface states near the TCP of another prototypical TQPT system (Bi1−δ Inδ )2 Se3 [75]. Therefore, these systematic and careful measurements on multiple systems suggest 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES that the observed preformed surface state is unlikely a special case due to material details of the BiTl(S1−δ Seδ )2 system but an important proximity phenomenon that describes the TCP in the electronic and spin groundstates in many TQPT systems. Our observation of preformed surface states can also be applied to explain a number of recent experiments on some newly predicted topological matter, such as the topological Kondo insulator phase predicted in SmB6 [118]. In SmB6 , the Kondo hybridization gap is believed to become significant below 30 K and the low temperature resistivity anomaly occurs below 6 K [50]. However, ARPES experiments have observed quasi-2D low energy states without kz dispersion persisting up to temperatures ≥ 100 K [50, 51]. Therefore, our observation of preformed surface states is critically important for developing a systemic theory in the vicinity of the TCP of a TQPT. For example, a recent theoretical effort proposed that the preformed surface states are due to the reversal of bulk Dirac fermion chirality across the TQPT [152], which is consistent with our systematic experimental data. Irrespective of their theoretical origin, our observation presents an interesting and surprising critical topological phase transition phenomenon. Our systematic data in this paper and hints from other works [49–51] suggest that the preformed surface states we identified here is a universal feature about the topological-critical-point in various topological phases. This important phenomenon has been largely missed (no theoretical prediction) before. These results set an inspiring experimental methodological paradigm for understanding how protected surface states in various topological materials arise from a conventional material. 76 Figure 3.10: Observation of gapped quasi-two-dimensional states prior to the topological-critical-point (TCP) of the topological quantum phase transition (TQPT). (a)-(c) ARPES kk -EB maps of BiTl(S1−δ Seδ )2 obtained using incident photon energy of 16 eV. The nominal composition values (defined by the mixture weight ratio between the elements before the growth) are noted on the samples. For (a) conventional band insulator (CBI), a band-gap is clearly observed for δ = 0.0 to 0.4; For (b) Compositions near the TCP of the TQPT, δ = 0.45, 0.50, 0.525 and 0.55; And for (c) topological band insulator (TBI), the conduction and valence bands are observed to be well-separated with the surface states connecting the band-gap for δ = 0.6 to 1.0. (d) The energy levels of the first-principles calculated bulk conduction and valence bands of the two end compounds (δ = 0.0 and 1.0) are connected by straight lines to denote the evolution of the bulk bands. The compositions selected for detailed experimental studies are marked by red arrows. The + and − signs represent the odd and even parity eigenvalues of the lowest lying conduction and valence bands of BiTl(S1−δ Seδ )2 . (e) Incident photon energy dependence spectra for δ = 0.45. (f ) kz vs kk Fermi surface maps for δ = 0.525 and 0.4. The kz range shown for δ = 0.4 samples corresponds to the incident photon energy from 14 eV to 26 eV. 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES Figure 3.10: textbf(g),(h) ARPES dispersion maps at various incident photon energy values for the compositions of δ = 0.4 < δc and δ = 0.525 ≃ δc . Some panels of this figure can also be found in Ref. [69]. Figure 3.11: Observation of spin-momentum locking behavior on the native Fermi level of the gapped quasi-2D states in the conventional semiconductor regime. (a) ARPES kk -EB map of BiTl(S1−δ Seδ )2 for a δ = 0.40 sample. Dotted line shows the binding energy where the spin-resolved measurements (d, e) are performed. (b) Momentum distribution curves (MDCs) of the dispersion map in panel (a). Highlighted MDC is chosen for spin-resolved measurements. (c) Fermi surface mapping for δ = 0.40. The two spin-resolved measurements are along the Γ̄-M̄ and Γ̄-K̄ cuts, respectively. Yellow arrows represent the measured spin polarization vectors around the Fermi surface. (d) Upper panel (left/right): measured in-plane spin-resolved momentum distribution spectra along the Γ̄-M̄ /Γ̄-K̄ cut. Lower panel (left/right): measured in-plane net spin polarization along the Γ̄-M̄ /Γ̄-K̄ cut. (e) same as panel (d) but for the out-of-plane component of the spin polarization. Some panels of this figure can also be found in Ref. [69]. 78 Figure 3.12 3.3 TOPOLOGICAL-CRITICAL-POINT AND THE “PREFORMED” SURFACE STATES Figure 3.12: Evolution of the quasi-2D states’ spin polarization with binding energy and composition. (a),(e),(i), ARPES kk -EB maps with dotted lines indicating the energy levels of spin-resolved measurements. Compositions of the samples are marked on the top of each map. (b),(f ),(j), MDCs with highlighted curves chosen for spin-resolved measurements. (c),(g),(k), Spin-resolved momentum distribution spectra, and (d),(h),(l), the corresponding net spin polarization measurements. Some panels of this figure can also be found in Ref. [69]. Figure 3.13: Near-surface band structure and spin polarization of BiTl(S1−δ Seδ )2 . (a), (b) Calculated electronic spectral weight distribution ((a)) and spin polarization ((b)) near the surface region of the constructed system are shown by the color maps in panels ((a) and (b)), respectively. The dispersion of the bulk bands are shown by the white (black) dotted lines. Positive band-gap means that the system lies in the conventional semiconductor (insulator) ν0 = 0 regime, whereas negative band-gap value means that the system lies in the topological insulator ν0 = 1 regime. (c) ARPES measured electronic dispersion on various δ values across the TQPT. The + and − signs in panels ((a) and (c)) represent the odd and even parity eigenvalues of the lowest lying conduction and valence bands of BiTl(S1−δ Seδ )2 . The red ↑ and ↓ arrows schematically show the in-plane spin polarization near the sample surface before and after the bulk band inversion (the TCP). Some panels of this figure can also be found in Ref. [69]. 80 Figure 3.14: A band-like schematic showing the phenomenological picture we proposed in the main text. The blue and green shaded areas represent the bulk conduction bands (BCB) and the bulk valence bands (BVB), which go through a band inversion at the critical point. The red lines represent electronic states that are strongly localized on the surface due to their minimal overlap with the bulk band continuum. The inner band (dotted lines) become bulk-like. One might worry about their singly degenerate nature, which is inconsistent with the doubly degenerate nature of the bulk bands. However, it is important to consider that there is another copy of these bands that has the opposite spin texture one the opposite surface of the sample. OLOGICAL PHASE TRANSITION AND “PREFORMED” CRITICAL BEHAVIOR IN (BI1−δ INδ )2 SE3 3.4 Topological phase transition and “preformed” critical behavior in (Bi1−δ Inδ )2Se3 Figure 3.15: Topological phase transition and “preformed” surface states in (Bi1−δ Inδ )2 Se3 . (a) ARPES dispersion maps at various In composition δ values. The critical point of the topological phase transition is about δc ∼ 0.04. (b) Dispersion of the composition δ = 0.06 sample repeated. The δ = 0.06 sample is found to be in the conventional semiconductor (topologically trivial) phase. The blue dotted lines define the momenta chosen for spin-resolved ARPES measurements. (c) Spin-resolved ARPES intensity and net spin polarization for the two spin-resolved cuts. Some panels can also be found in Ref. [75]. We note that the topological phase transition from a conventional band insulator to a 3D Z2 TI can be realized in another material, namely (Bi1−δ Inδ )2 Se3 [75]. Here, again, the crystal structure remains the same throughout the whole range of the chemical composition δ. Fig. 3.15(a) shows the ARPES dispersion maps of the (Bi1−δ Inδ )2 Se3 system at various In composition δ values, where a topological phase 82 transition is clearly seen. The critical composition for this system is found to be about δ = 0.04 [75]. In Figs. 3.15(b),(c), we show a composition (δ = 0.06) that is in the trivial regime, where a small band-gap is found. Fig. 3.15(c) shows the spin-resolved ARPES data near the Fermi level of the δ = 0.06 sample. Clear spin polarization is observed. Furthermore, the spin polarization is found to reverse as one goes from one side of the Fermi surface (cut1) to the other (cut2). These data show the observation of preformed surface states in the (Bi1−δ Inδ )2 Se3 system. This finding strongly suggests that the preformed surface state is not a special case in the BiTl(S1−δ Seδ )2 system but an important proximity phenomenon that describes the TCP in the electronic and spin groundstates in many TQPT systems. In the following chapters, we will also discuss the topological phase transition in a topological crystalline insulator (TCI) phase in the Pb1−δ Snδ Te(Se) system and the associated phenomena in a topological Kondo insulator (TKI) candidate SmB6 . This Chapter gives a general experimental guideline for how topological state and its protected surface states can emerge from a conventional material by going through a topological quantum phase transition. Chapter 4 Topological Crystalline Insulator Phase in Pb1−δ Snδ Te(Se) A topological crystalline insulator is a new topological phase where space group symmetries replace the role of time-reversal symmetry in a Z2 (Kane-Mele) topological insulator. In this chapter, we present our experimental identification of a topological crystalline insulator state (TCI) in the Pb1−δ Snδ Te(Se) systems, marking the first realization of the topological crystalline insulator phase in real materials. In the first section, we briefly review the key theoretical concepts for a TCI state. Then we present the realization of a TCI state protected by the mirror symmetries in Pb1−δ Snδ Te. Particularly, our surface state spin texture data provide a direct experimental measurements of its topological number (the mirror Chern number nM ). Finally in the last section, we show systematic ARPES studies on the surface state electronic structure of a similar TCI compound Pb1−δ Snδ Se, where a saddle point surface electronic structure singularity is directly resolved. Our ARPES and spin-resolved ARPES measurements identified the topological crystalline insulator (TCI) phase protected by the mirror symmetries in the Pb1−δ Snδ Te, and further experimentally revealed its topological number, the mir84 ror Chern number, nM = −2. The observed topological surface states serve as a new type of 2D electronic gas, which is distinct from both a regular 2DEG and the surface states in a Z2 TI. The new crystalline surface states pave the way for many uniquely-new quantum phenomena, including surface spin filtering, strain-induced crystalline symmetry protected Chern currents [153–156]. As a result, these new topological surface states that we observed in Pb1−δ Snδ Te have attracted interest by many others and now studied by other experimental techniques (transport, STM, etc.) [42,95,152,157–169], Our experimental work marks the first realization of a TCI phase in realistic materials, and many other TCIs with yet more exotic properties await their discoveries. 4.1 Key theoretical concepts for a topological crystalline insulator state As we have elaborated before (see Chapter 1.4.2), to construct a new topological state beyond a Z2 topological insulator, there are three steps (1) identify a material with a finite number of band inversions between the bulk conduction and valence bands, (2) identify a symmetry that can protect a surface state band crossing at certain momentum space locations in the surface BZ, (3) identify the momentum space locations for the band inversions and the symmetry protection coincide, so a protected surface state with a surface band crossing is realized within the inverted band-gap. Thus the existence of band inversion (step 1) only provides a necessary but not sufficient condition for giving rise to a topological phase. Steps 2 and 3, on the other hand, determine the topological nature (the topological number) of a material system. Let us take the BiTl(S1−δ Seδ )2 discussed in the previous section as an example: by going from the sulfur end (δ = 0) to the selenium end (δ = 1), the bulk bands go KEY THEORETICAL CONCEPTS FOR A TOPOLOGICAL CRYSTALLINE INSULATOR STATE through a band inversion at the center of the BZ top (111) surface T point. At the (111) surface, the T point projects onto the surface BZ center Γ̄ point, which is a Kramers point protected by the time-reversal symmetry. Therefore, the inverted side (δ > 0.5) of the BiTl(S1−δ Seδ )2 is a Z2 topological insulator. Now a key question to ask is ”Can we identify other types of symmetries that can also protect a surface state band-crossing (e.g. a surface Dirac point) within an inverted band-gap?” That will certainly lead to a new topological state since the relevant symmetry is changed from time-reversal to others. Since we are working with solid state crystals, an obvious choice of symmetry is the space group symmetries of a crystalline system. The issue of what kind of crystalline space group symmetries can protect surface state band-crossing has been theoretically addressed by the following works [116, 117, 171]. Currently, theory has identified three-distinct crystalline symmetries that can protect topological surface states. However, we also note that no one has proven that the existing three are the only possible symmetries for realizing a TCI state. Rather, this is still an active on-going theoretical research. The three known symmetries to protect surface state band-crossings in a TCI state are: • Mirror symmetry M. This results in a Z classification, where the topological number is a mirror Chern number that can be any integer [117, 170]. • C4 rotational symmetry + time-reversal symmetry without spin-orbit coupling (spinless fermionic systems). This results in a Z2 classification, where the Z2 topological number can be 0 or 1 [116]. • Cnv symmetry + time-reversal breaking without spin-orbit coupling (spinless fermionic systems). This results in a Z classification, where the topological number can be any integer [171]. We briefly introduce the key theoretical concepts for the mirror symmetry type of TCI state, which will be the focus of our experimental work. Let us take an example, 86 Figure 4.1: (a) A bulk BZ with a mirror (yellow) plane. (b) The surface (blue and red solid lines) and bulk (grey shaded area) electronic structure alone the mirror plane. in which a crystal has a bulk BZ as shown in Fig. 4.1(a), where the ky = 0 plane (the yellow plane) is a mirror plane for the system. The fact that the kx − kz plane is a mirror plane means the system is invariant under the mirror reflection with respect to ky = 0, where M(ŷ) = P C2 (ŷ). This immediately implies that all the bulk electronic states in the plane ky = 0 can be labeled with a mirror eigenvalue ±i [170]. Now suppose that the bulk electronic structure within this 2D plane has a full energy gap, then it is possible to assign a Chern number for the occupied energy bands for each mirror eigenvalue: n±i −i = 2π Z ky =0 [∇k × < u±i (k)|∇|u±i (k) > (kx , kz )]z d2 k, (4.1) where the bulk electronic wavefunction |u±i (k) > is labeled by its mirror eigenvalue. The total Chern number of the occupied bands is n = n+i + n−i . In a time-reversal symmetric system, one has n = 0. However, one can define a mirror KEY THEORETICAL CONCEPTS FOR A TOPOLOGICAL CRYSTALLINE INSULATOR STATE Chern number as: nM = (n+i − n−i )/2 (4.2) Further theoretical analysis has shown that the mirror Chern number nM is a topological invariant under the condition that the mirror symmetry is preserved in the system [117, 170]. With these theoretical foundations, one could consider the band structure at ky = 0 as two sets of band structures labeled by their different mirror eigen values ±i. These two sets are related by the mirror symmetry operation M(ŷ). For each set, let’s say mirror eigenvalue of +i, the band structure has a well defined Chern number n+i . Thus we can conceptually view it has a Chern insulator, where at the 1D boundary there are |n+i | altogether chiral edge states. Since we assume time-reversal symmetry, we have n−i = −n+i . Therefore, for the sets of bands with mirror eigenvalue −i, there will be the same number (|n+i | = |n−i |) of chiral edge states but moving to the opposite direction since n−i = −n+i . These edge states should have the same mirror eigen value (+i or −i) as their corresponding bulk bands, which means the counterpropagating edge states must have the opposite mirror eigen values. Therefore, the edge band-crossing between two counterpropagating edge states at the mirror plane ky = 0 must be protected by the mirror symmetry. Because if one can add a term that will gap out the band-crossing (degeneracy) between these two counterpropagating edge states, that term must break the mirror symmetry. Any term that respects the mirror symmetry only shifts the crossing in energy within the mirror plane. Fig. 4.1(b) presents a case of n+i = 1 and n−i = −1. Thus one has one right-going (red) edge state derived from the mirror eigenvalue +i bulk bands and one left-going (blue) edge state derived from the mirror eigenvalue −i bulk bands. Their edge band-crossing is protected by the mirror symmetry with a mirror Chern number nm = +1. A similar argument applies to Fig. 4.1(c). We note that the mirror symmetry at ky = 0 only requires the edge band-crossing to be within the ky = 0 88 plane. In principle, perturbations that respect the mirror symmetry can shift the band-crossing along the energy axis and also only the momentum kx , as long as the band-crossing stays within the ky = 0 mirror symmetry plane and the bulk bandgap along the energy-axis. Thus the schematics in Figs. 4.1(b),(c), where the edge band-crossing is at the Γ̄ point kx = 0 is just a special case. 4.2 Discovery of mirror symmetry protected TCI state in Pb1−δ Snδ Te In this section, we present the realization of a TCI state protected by the mirror symmetries in Pb1−δ Snδ Te. Particularly, our surface state spin texture measurements provide a direct experimental measure for its topological number (the mirror Chern number nM ). 4.2.1 Band inversions and mirror symmetries in Pb1−δ Snδ Te The Pb1−δ Snδ Te pseudo-binary alloy system crystallizes in the sodium chloride crystal structure, (space group Fm3̄m (225)). In this structure, each of the two atom types (Pb/Sn, or Te) forms a separate face-centered cubic lattice, with the two lattices interpenetrating so as to form a three-dimensional checkerboard pattern. The first Brillouin zone (BZ) of the crystal structure is a truncated octahedron with six square faces and eight hexagonal faces. The band-gap of Pb1−δ Snδ Te is found to be a direct gap located at the L points in the BZ [172]. The L points are the centers of the eight hexagonal faces of the BZ. Due to the inversion symmetry of the crystal, each L point and its diametrically opposite partner on the BZ are completely equivalent. Thus there are four distinct L point momenta. It is well established that the band inversion transitions in the Pb1−δ Snδ Te take place at the four L points of the BZ [173–175]. As a result, an even number (four) of inversions exclude the system from being a 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE Figure 4.2: Band inversion transitions and mirror symmetries in Pb1−δ Snδ Te. (a) The lattice of the Pb1−δ Snδ Te system is based on the sodium chloride crystal structure. (b) The first Brillouin zone (BZ). The mirror planes are shown using green and light-brown colors. These mirror planes project onto the (001) crystal surface as the X̄ − Γ̄ − X̄ mirror lines (shown by red solid lines). (c) ARPES measured core level spectra (incident photon energy 75 eV) of two representative compositions, namely Pb0.8 Sn0.2 Te and Pb0.6 Sn0.4 Te. (d) The bulk band-gap of Pb1−δ Snδ Te alloy system undergoes a band inversion upon changing the Pb/Sn ratio at each L point in the bulk BZ [172–175]. (e), (f ) First-principles based calculation of band dispersion (e) and iso-energetic contour with energy set 0.02eV below the Dirac node energy (f ) of the inverted end compound SnTe. This figure is adapted from Ref. [40]. Kane-Mele Z2 topological insulator [2]. However, it is interesting to note that the momentum-space locations of the band inversions coincide with the momentum-space mirror plane within the BZ. These facts suggest that the inverted Pb1−δ Snδ Te may realize a distinct TCI state protected by mirror symmetry. Before we go into further details, it is worth noting that before Pb1−δ Snδ Te was discussed, many known Z2 TIs (such as Bi0.91 Sb0.09 , Bi2 Se3 ) also featured nonzero mirror Chern number [31]. This is in fact quite intuitive. Let us take Bi2 Se3 as an example. It has a single bulk band inversion at the BZ center Γ point. For a bulk 90 4.2.2 Topological surface states in Pb0.6 Sn0.4 Te BZ corresponding to a rhombohedral crystal structure, it has 3 distinct mirror planes along the (111) direction which goes through the Γ point. Therefore, Bi2 Se3 has a mirror Chern number of |nM | = 1 (the sign of the mirror Chern number needs further investigation based on the surface state spin texture). However, the key here is that there are four (an even number of) bulk band inversions in Pb1−δ Snδ Te, which exclude a nonzero Z2 topological number. Thus any nonzero mirror Chern number that might realize in Pb1−δ Snδ Te is not “masked” by a finite Z2 number unlike in Bi2 Se3 . This realizes a distinct TCI state without ambiguity. Let us try to evaluate the possible TCI state and the associated mirror Chern number in Pb1−δ Snδ Te before going into experimental data or theoretical calculations. As shown in Fig. 4.2(b), each mirror plane contains two distinct L points and thus two bulk band inversions per BZ. If we intuitively assume that each band inversion changes the mirror Chern number by 1, then we immediately get that |nM | = 2 for Pb1−δ Snδ Te. 4.2.2 Topological surface states in Pb0.6Sn0.4Te In order to identify the mirror-nontrivial TCI state, we perform systematic ARPES and spin-ARPES measurements to search for mirror symmetry protected surface states in inverted compositions of the Pb1−δ Snδ Te system. In order to capture the electronic structure both below and above the band inversion transition (theoretically predicted to be around δ ≃ 1/3 [173, 174]), we choose two representative compositions, namely δ = 0.2 and δ = 0.4 for detailed systematic studies. Fig. 4.2(c) shows the momentum-integrated core level photoemission spectra for both compositions. Photoemission peaks corresponding to tellurium 4d, tin 4d, and lead 5d orbitals are observed in Fig. 4.2(c). The energy splitting of the Pb orbital is observed to be larger than that of the Sn orbital, which is consistent with the stronger spin-orbit coupling of the heavier Pb nuclei. In addition, the spectral 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE intensity contribution of the Sn peaks in the δ = 0.4 sample (red) is found to be higher than that of in the δ = 0.2 sample (blue), which is also consistent with the larger Sn concentration in the δ = 0.4 samples. We performed systematic low energy electronic structure studies on these two representative compositions. Since the low energy physics of the system is dominated by the band inversion at X̄ points on the (001) surface, we present ARPES measurements with the momentum space window centered at the X̄ point, which is the midpoint of the surface BZ edge. Figs. 4.3(a),(b) show the ARPES Fermi surface and dispersion mappings of the Pb0.8 Sn0.2 Te sample (δ = 0.2). The system at δ = 0.2 is observed to be gapped: No band is observed to cross the Fermi level in the Fermi surface maps [Fig. 4.3(a)]. The dispersion measurements [Fig. 4.3(b)] reveal a single hole-like band below the Fermi level. This single hole-like band is observed to show strong dependence with respect to the incident photon energy [Fig. 4.4(a)], which reflects its three-dimensionally dispersive bulk valence band origin. As a qualitative guide to the ARPES measurements on δ = 0.2, we present first-principles based electronic structure calculation on the non-inverted end compound PbTe [Fig. 4.3(c)]. Our calculations confirm that PbTe is a conventional band insulator, whose electronic structure can be described as a single hole-like bulk valence band in the vicinity of each X̄ point, which is consistent with our ARPES results on Pb-rich Pb0.8 Sn0.2 Te. The three-dimensional nature of the calculated bulk valence band is revealed by its kz evolution in Fig. 4.3(c), which is in qualitative agreement with the incident photon energy dependence of our ARPES measurements shown in Fig. 4.3(b). Now we present comparative ARPES measurements under identical experimental conditions and setups on the Pb0.6 Sn0.4 Te (δ = 0.4) sample. In contrast to the conventional band insulator (insulating) behavior in the δ = 0.2 sample, the Fermi surface mapping [Fig. 4.3(d)] on the δ = 0.4 sample shows two unconnected metallic Fermi pockets (dots) on the opposite sides of the X̄ point. The dispersion measurements 92 4.2.2 Topological surface states in Pb0.6 Sn0.4 Te on the δ = 0.4 sample are shown in Fig. 4.3(e). The single hole-like bulk valence band, which is similar to the δ = 0.2 conventional band insulator composition, is also observed below the Fermi level. More importantly, a pair of metallic states crossing the Fermi level on the opposite sides of the X̄ point is observed along the Γ̄ − X̄ − Γ̄ mirror line momentum space direction. These states are found to show no observable dispersion upon varying the incident photon energy [Fig. 4.4(a)], reflecting its twodimensional character. On the other hand, the single hole-like band, similar to the one seen in δ = 0.2 samples, is observed to disperse strongly upon varying the incident photon energy, suggesting its three-dimensional character. At a set of different photon energy values (effectively probing different kz values), the bulk valence band intensity overlaps (intermixing) with different parts of the surface states in energy and momentum space: At a photon energy of 18 eV, the intermixing (intensity overlap) is strong, and the inner two branches of the surface states are masked by the bulk intensity. At photon energies of 10 eV and 24 eV, the surface states are found to be relatively better isolated. These ARPES measurements shown in Figs. 4.3(d),(e) suggest that the δ = 0.4 sample lies in the inverted composition regime and that the observed surface states are related to the band inversion transition in Pb1−δ Snδ Te system as predicted theoretically [117, 175]. As a qualitative guide, we present firstprinciples based electronic structure calculation on the inverted end compound SnTe [Fig. 4.3(f)]. The calculated electronic structure of SnTe is found to be a superposition of two kz nondispersive metallic surface states and a single hole-like kz dispersive bulk valence band in the vicinity of the X̄ point, which is in qualitative agreement with the ARPES results on Pb0.6 Sn0.4 Te. We now perform systematic measurements on the surface electronic structure of the Pb0.6 Sn0.4 Te. Fig. 4.5(b) shows the wide range iso-energetic contour mapping covering the first surface BZ. The surface states are observed to be present, and only present, along the mirror line (Γ̄ − X̄ − Γ̄) directions. No other states are found along 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE any other momentum directions on the Fermi level. In close vicinity to each X̄ point, a pair of surface states are observed along the mirror line direction. One lies inside the first surface BZ but the other is located outside. Therefore, in total, four surface states are observed within the first surface BZ, which is in agreement with the fact that there are four band inversions in the Pb1−δ Snδ Te system. The mapping zoomedin near the X̄ point [Fig. 4.5(c)] reveals two unconnected small pockets (dots). The momentum space distance from the center of each pocket to the X̄ point is about −1 0.09 Å . Dispersion measurements (EB vs k) are performed along three important momentum space cuts, namely cuts 1, 2, and 3 defined in Fig. 4.5(b), in order to further reveal the surface states electronic structure. Metallic surface states crossing the Fermi level are observed in both cuts 1 and 2, whereas cut 3 is found to be fully gapped. In cut 1 Fig. 4.5(d), which is the mirror line (Γ̄ − X̄ − Γ̄) direction, a pair of surface states are observed on the Fermi level. We also study the dispersion along cut 2 Fig. 4.5(d), which only cuts across the surface states inside the first surface BZ. Both the dispersion maps and the momentum distribution curves in cut 2 reveal that the surface states along cut 2 are nearly Dirac-like (linearly dispersive) close to the Fermi level. The surface states’ velocity is obtained to be 2.8±0.1 eV·Å (4.2 ± 0.2 ×105 m/s) along cut 2, and 1.1±0.3 eV·Å (1.7 ± 0.4 ×105 m/s) for the two outer branches along cut 1, respectively. We highlight the following results from our data relevant to the topological nature of the surface states: (1) there are in total 4 surface states within a surface BZ [Fig. 4.5(b)], (2) none of the surface states enclose a Kramers point [Fig. 4.5(b)], (3) all surface states locate alone the mirror symmetry (Γ̄ − X̄ − Γ̄ direction. The first two points show that these surface states do not arise from a Z2 topological number. Thus the Pb1−δ Snδ Te system is Z2 topological trivial. The three points are consistent with a mirror symmetry protected TCI state. 94 4.2.2 Topological surface states in Pb0.6 Sn0.4 Te Figure 4.3: Comparison of non-inverted and inverted compositions. (a),(b) ARPES low energy electronic structure measurements on Pb0.8 Sn0.2 Te (δ = 0.2). (c) First-principle calculated electronic structure of PbTe (δ = 0) as a qualitative guide to the ARPES measurements on Pb0.8 Sn0.2 Te. (d),(e) ARPES low energy electronic structure measurements on Pb0.6 Sn0.4 Te (δ = 0.4) under the identical experimental conditions and setups as in (a and b). (f ) First-principle calculated electronic structure of SnTe (δ = 1) as a qualitative guide to the ARPES measurements on Pb0.6 Sn0.4 Te. 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE Figure 4.4: Comparison of non-inverted and inverted compositions at different incident photon energies. ARPES dispersion maps and the corresponding momentumdistribution curves (MDCs) at different incident photon energies for both the non-inverted (δ = 0.2) and the inverted (δ = 0.4) compositions. 96 4.2.2 Topological surface states in Pb0.6 Sn0.4 Te Figure 4.5: Mirror protected surface states in Pb0.6 Sn0.4 Te. (a) First-principle calculated surface states of SnTe with energy set 0.02eV below the Dirac node energy are shown in red. (b) Left panel: ARPES iso-energetic contour mapping (EB = 0.02 eV) of Pb0.6 Sn0.4 Te covering the first surface Brillouin zone (BZ) using incident photon energy of 24 eV. Right panel: Spectral intensity distribution as a function of momentum along the horizontal mirror line (defined by ky = 0). (c) High resolution Fermi surface mapping (EB = 0.0 eV) in the vicinity of one of the X̄ points. (d)-(f ) Dispersion maps (EB vs k) and corresponding energy (momentum) distribution curves of the momentum space cuts 1, 2, and 3. The momentum space cut-directions of cuts 1, 2, and 3 are defined by the blue dotted lines in panel (c). The second derivative image (SDI) of the measured dispersion is additionally shown for (d). This figure is adapted from Ref. [40]. 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE 4.2.3 Mirror Chern number and mirror symmetry protection In order to experimentally probe the topological number in the Pb1−δ Snδ Te system, we measure the spin texture of the surface states as shown in Fig. 4.6. Our spinresolved measurements are performed along the mirror line (Γ̄ − X̄ − Γ̄) direction as shown in Fig. 4.6(a), since the electronic and spin structure along this direction is most critically relevant to the TCI phase [117]. Considering that the natural Fermi level of our δ = 0.4 samples is very close to the Dirac point (which is spin degenerate), the spin polarization of the surface states are measured at 60 meV below the Fermi level in order to gain proper contrast, namely SR-Cut 1 in Fig. 4.6(a). As shown in the net spin polarization measurement of SR-Cut 1 in Fig. 4.6(c), in total four spins pointing in the (±) in-plane tangential direction are revealed for the surface states along the mirror line direction. This is consistent with the observed two surface state cones (four branches in total) near an X̄ point along the mirror line direction. To compare and contrast the spin polarization behavior of the surface states (SR-Cut 1) with that of the bulk states, we perform spin-resolved measurement SR-Cut 2 at EB = 0.70 eV, where the bulk valence bands are prominently dominated. The surface states are well-defined at lower binding energies (approximately below 0.3 eV or so) where they emerge out of the bulk states and merge with the bulk band at high binding energies. Indeed, in contrast to SR-Cut1 reflecting the surface states’ spin polarization, no significant net spin polarization is observed for SR-Cut2. This is expected for the bulk valence bands of the inversion symmetric Pb1−δ Snδ Te system. Now we use the obtained electronic and spin structure of the surface states along the mirror line direction to obtain the topological number of the Pb1−δ Snδ Te system. As shown in Figs. 4.3-4.6, along each mirror line, there are two Dirac surface states within a surface BZ. Our spin polarization measurements in Fig. 4.6(c) further show that these surface states are singly degenerate. These facts demonstrate that the absolute value of the mirror Chern number is 2, |nM | = 2. The sign of the mirror 98 4.2.3 Mirror Chern number and mirror symmetry protection Chern number can be determined by the handedness (chirality) of the surface state spin texture as shown in Fig. 4.6(f). Specifically, at an energy below the surface Dirac point, if the Fermi surface spin texture is left-handed, then nM = 2; If Fermi surface spin texture is right-handed, then nM = −2. As shown in Fig. 4.6(c), our spin-resolved measurements show that the spin texture profile is right-handed at EB = 0.06 eV, which is below the surface Dirac point. Therefore, we conclude from our experimental data that the TCI state in the Pb1−δ Snδ Te system has a mirror Chern number (its topological number of nM = −2. We provide a conceptual picture to visualize the mirror symmetry protection for the surface states observed in the TCI Pb0.6 Sn0.4 Te system. As shown in Fig. 4.2(b), at the (001) surface, each X̄ point is in fact the projection of two distinct L points (therefore two band inversions). If we intuitively assume that each bulk band inversion gives rise to a surface Dirac cone whose Dirac band crossing is at each X̄ point, then two bulk band inversions will lead to two surface Dirac cones at each X̄ point, where the energies of the two Dirac points have an offset, as shown in Fig. 4.2(c). The surface state Fermi surface (without considering the hybridization between the two cones) is a circle [see first panel of Fig. 4.2(c)]. These two surface Dirac cones can hybridize. Without, any additional symmetry, hybridization will open up an energy gap everywhere on the circular-like surface band-crossing and therefore the system will be fully gapped (topologically trivial). However, if we consider a mirror plane along the Γ̄ − X̄ − Γ̄ direction, then the surface state band-crossing is protected along the mirror line and the resulting surface electronic structure is a “two Dirac cones along the Γ̄ − X̄ − Γ̄ mirror line direction” state, which is consistent with our experimental data. We present a comparison of the Pb0.6 Sn0.4 Te and a single Dirac cone Z2 topological insulator (TI) system. As shown in Fig. 4.2(a), for a Z2 TI, a single surface Dirac cone is observed enclosing the time-reversal invariant Kramers’ momenta Γ̄ in both ARPES and calculation results, demonstrating its Z2 topological insulator state and 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE the time-reversal symmetry protection of its single Dirac cone surface states. On the other hand, for the Pb0.6 Sn0.4 Te samples [Fig. 4.2(b)], none of the surface states is observed to enclose any of the Kramers points. On the other hand, all surface states locate along the mirror line directions. We note that one advantage of the Pb1−δ Snδ Te system is that it can be easily doped with manganese, thallium, or indium to achieve bulk magnetic or superconducting states [165–169]. The symmetry in the Pb1−δ Snδ Te system (its nonmagnetic character) can be broken by magnetic or superconducting doping into the bulk or the surface. In future experiments, it would be interesting to explore the modification of our observed surface states brought out by magnetic and superconducting correlations, in order to search for exotic magnetic and superconducting order on the surface. Such magnetic and superconducting orders on the surface states in Pb1−δ Snδ Te can be different from those recently observed in theZ2 topological insulators [57, 58] due to its very distinct topology of surface electronic structure. The novel magnetic and superconducting states to be realized with this novel topology are not strongly related to the question of gapless or gapped nature of the TCI phase. Therefore our observation of the spin-polarized surface states presented here provides the much desired platform for realizing unusual surface magnetic and superconducting states in future experiments. 100 4.2.3 Mirror Chern number and mirror symmetry protection Figure 4.6: Experimental measurement of the mirror Chern number. (a) ARPES dispersion map along the mirror line direction. The white dotted lines show the binding energies chosen for spin-resolved measurements SR-Cut 1 at EB = 0.06 eV and SR-Cut 2 EB = 0.70 eV respectively. Inset: Measured spin polarization are shown by the green and blue arrows on top of the ARPES iso-energetic contour at binding energy EB = 0.06 eV for SR-Cut1. (b),(c) Measured in-plane spin-resolved intensity (b) and in-plane spin polarization (c) of the surface states (SR-Cut 1) near the Fermi level at EB = 0.06 eV. (d),(e) Measured in-plane spin-resolved intensity (d) and in-plane spin polarization (e) of the bulk valence bands (SR-Cut 2) at high binding energy at EB = 0.70 eV. f, Surface spin texture configurations corresponding to mirror Chern number of nM = 2 and nM = −2. g, Theoretically expected spin polarization configuration of the surface states which corresponds to a mirror Chern number) nM = −2. 4.2 DISCOVERY OF MIRROR SYMMETRY PROTECTED TCI STATE IN PB1−δ SNδ TE Figure 4.7: Mirror symmetry protection and a comparison of Z2 (Kane-Mele) topological insulator and topological crystalline insulator (TCI) phases. (a) ARPES and calculation results of the surface states of a Z2 topological insulator GeBi2 Te4 , an analog to Bi2 Se3 [32]. b, ARPES measurements on the Pb0.6 Sn0.4 Te (x = 0.4) samples and band calculation results on the end compound SnTe. (c) A conceptual picture to visualize the mirror symmetry protection for the surface states observed in the TCI Pb0.6 Sn0.4 Te system. 102 4.3 Topological surface states in Pbδ Sn1−δ Se In this chapter, we systematically study the electronic structure of the topological surface states in TCI phase in Pbδ Sn1−δ Se. We present our observation of a range of novel electronic properties in these surface states, including Lifshitz transition, saddle point singularities, temperature-driven topological phase transition, etc. 4.3.1 Lifshitz transition and saddle point singularities Saddle point singularities in two-dimensional Dirac electron gas often results in electronic instabilities leading to exotic correlated quantum phenomena. A notable example is the extensive research efforts on the van Hove singularity in graphene, where d-wave superconductivity and unusual magnetism or Kondo effect have been predicted to take place [176–179]. Very recently, striking Hofstadter butterfly spectrum and fractional quantum Hall effect have been experimentally observed in twisted graphene system due to the saddle point singularity in its Dirac band structure, which further adds to the interest [180, 181]. Like graphene, the surface states of topological insulators (TIs) also possess the light-like Dirac dispersion. What is more interesting is that the Dirac surface states of TIs are spin-momentum locked, since they are a consequence of the bulk band inversions and the nontrivial topology of the bulk electronic band structure. As a result, saddle point singularities in topological surface states (a spin-helical two-dimensional Dirac electron gas) are even more exotic because they not only host correlated physics, but also allow one to explore the coexistence and the interplay between topological order and strong correlation. While none of the surface states in any known Z2 TI materials satisfy the conditions to realize a Lifshitz transition, the newly identified TCI surface states in the Pbδ Sn1−δ Se(Te) system in fact provide an ideal platform. As we have shown in the previous section, the (001) surface states in Pbδ Sn1−δ Se(Te) 4.3 TOPOLOGICAL SURFACE STATES IN PBδ SN1−δ SE can be described by a pair of surface Dirac cones in the vicinity of each X̄ point. We have also observed such type of surface states in the inverted composition (δ = 0.3) of the Pbδ Sn1−δ Se system, as shown in Fig. 4.8. Moreover, in Pb0.7 Sn0.3 Se, the samples are in fact n-type and thus the upper Dirac surface bands are also observed. Fig. 4.8(e) shows the ARPES dispersion map along the Γ̄ − X̄ − Γ̄ mirror line direction, where two Dirac surface states near an X̄ point is clearly visualized. The energy evolution of the surface state constant energy contour is shown in Fig. 4.8(c). Two Dirac points are observed sitting at the same energy EB = 70 meV [central penal of Fig. 4.8(c)] near the X̄ point along the Γ̄ − X̄ − Γ̄ momentum space cut-direction in the surface BZ. As the energy is tuned away from the Dirac points, the two Dirac points grow into two unconnected pockets, and eventually “meet” each other, where they are found to become two concentric contours both enclosing the X̄ point. Therefore a surface state Lifshitz transition is observed in our data since the constant energy contour is found to undergo a topological change. Thus there exist two Lifshitz transitions at EB = 40 meV and EB = 98 meV. These Lifshitz transitions are expected to lead to saddle point band structure singularities at the same energies. In order to demonstrate the singularity, we systematically study the electronic structure at the Lifshitz transition energy (EB = 40 meV), as shown in Fig. 4.9. The two square markers in Fig. 4.9(a) note the momentum space locations, where the two unconnected contours merge. Their energy and momentum space coordinates are experimentally identified to be −1 (EB , kx , ky ) = (40 meV, 0, ±0.02 Å ). To experimentally prove the saddle points in momentum-space band structure, we focus on the upper blue square in Fig. 4.9(a) and study the energy-momentum dispersion cuts along three important momentum space cut-directions, namely cuts 1,2, and 3. Cuts 1 and 2 [Figs. 4.9(c),(d)] are along the horizontal (kx ) and verticle (ky ) directions across the blue square. Interestingly, the blue square is found to be a local band structure minimum along cut1 shown in Fig. 4.9(c), whereas it is a local maximum along cut2 [Fig. 4.9(d)]. Observation of 104 4.3.1 Lifshitz transition and saddle point singularities local minimum and local maximum at the same momentum space location (the blue square) manifestly shows that it is a surface band structure saddle point. The observation of surface momentum-space saddle point immediately implies that there exist certain intermediate cut-directions (between cuts 1 and 2), where the surface band structure is completely flat in the vicinity of the blue square. Indeed, as shown in Fig. 4.9(e), for cut 3, we found that the surface states are nearly flat near the saddle point. The observed flat band structure (along cut 3) may give rise to the divergence of the surface density of states (DOS), leading to surface van Hove singularity. We first present the theoretically calculated momentum-integrated DOS of the TCI surface states. As shown in Fig. 4.8(b), two DOS peaks are found, which correspond to the van Hove singularities in the upper and lower parts of the Dirac cones, respectively. Additionally, three dips in the calculated DOS curve correspond to the two Dirac points, as well as the upper and lower Dirac points (UDP and LDP) [Fig. 4.8(a)]. In order to search for experimental evidence of van Hove singularities, we study the momentum-integrated ARPES intensity as shown in Fig. 4.8(e). Indeed, a pronounced peak is observed at the energy corresponding to the saddle point, namely EB = 40 meV, as labeled by “VH1” in Fig. 4.8(e). Additionally, we observe a significant dip of ARPES intensity at the binding energy of EB = 70 meV, which corresponds to the energy of the Dirac points. In order to better highlight other important features, we take the second derivative of the ARPES intensity [Fig. 4.8(f)], which allows all five features to be visualized. 4.3 TOPOLOGICAL SURFACE STATES IN PBδ SN1−δ SE Figure 4.8: Observation of the Lifshitz transition in the topological surface states in Pb0.7 Sn0.3 Se. (a) ARPES dispersion maps upon in situ Sn deposition on the Pb0.70 Sn0.30 Se surface. The dosage (time) for Sn deposition is noted. A different batch of sample, which is p−type with the chemical potential below the Dirac points, is used for the Sn deposition data shown in this panel. (b),(c) Schematics of surface band dispersion of the TCI phase along the mirror line Γ̄ − X̄ − Γ̄ and the M̄ − X̄ − M̄ momentum space cut-directions. Five important features of the surface states, including Dirac point of the upper part of the Dirac cones (UDP), van Hove singularity of the upper Dirac cones (VH1), two Dirac points along the Γ̄ − X̄ − Γ̄ mirror line (DP), van Hove singularity of the lower part of the Dirac cones (VH2) and Dirac point of the lower part of the Dirac cones (LDP) are marked. (c) Calculated density of state (DOS) for the surface states and the bulk bands using the k · p model [151]. (d) Experimental observation of the Lifshitz transition - the binding energies are noted on the constant energy contours. 106 4.3.1 Lifshitz transition and saddle point singularities Figure 4.8: (e) ARPES measured dispersion plots along Γ̄ − X̄ − Γ̄ and M̄ − X̄ − M̄. (f ) Momentum (kx and ky ) integrated ARPES intensity as a function of binding energy (left). 2nd derivative of the ARPES intensity with respect to binding energy is presented to further highlight the features. The upper Dirac point (UDP), upper van Hove singularity (VH1), Dirac point (DP), lower van Hove singularity (VH2) and lower Dirac point (LDP) are marked. This figure is adapted from Ref. [81]. Figure 4.9: Observation of the saddle point singularity. (a) ARPES constant energy contour map in the vicinity of an X̄ point in the surface (001) BZ at binding energy 40 meV, which corresponds to the surface Lifshitz transition and saddle point energy of the upper part of the Dirac cones. The blue and green squares denote the momentum space locations of the two surface saddle points. The blue dotted lines indicates the momentum space cut-directions for cuts1, 2, and 3, which are centered at the blue square. (b) Calculated surface state constant energy contour at the saddle point singularity energy (top) and a three-dimensional schematic of a saddle point (bottom). (c)-(e) ARPES dispersion maps (left) and their second derivative images along cuts 1, 2, and 3. The white and green arrow point the saddle points [blue and green squares in Panel (a)]. This figure is adapted from Ref. [81]. 4.3 TOPOLOGICAL SURFACE STATES IN PBδ SN1−δ SE 4.3.2 Temperature-driven topological phase transition Interestingly, we found that in the Pbδ Sn1−δ Se system, a topological phase transition from a TCI phase to a trivial phase can be realized not only by changing the chemical composition δ (as in BiTl(S1−δ Seδ )2 ), but also simply by varying the temperature T . Fig. 4.10 shows the ARPES measurements of the TCI surface states in Pb0.70 Sn0.30 Se at various tempeatures. At low temperature of T = 20 K, two Dirac cones are observed near the X̄ point along the Γ̄ − X̄ − Γ̄, which is evident in the nontrivial TCI phase. Interestingly, as the temperature is raised to 100K, the two Dirac points are found to move closer to each other. With further increase in the temperature, the two cones are observed to merge at temperature around 250 K at the X̄ point. Finally a gap at the Dirac point is opened for T > 250 K, which suggests that the system enters the topologically trivial phase. In order to understand the interesting thermal evolution of the surface state electronic structure, we perform first principle theoretical calculations at different lattice constant values [Fig. 4.10(b)]. A reasonably good agreement between the temperature dependent ARPES data and the lattice constant dependent calculation is found, where the essential features of the data, including the two Dirac cones approaching, merging and eventually opening up a gap, are all captured in the calculation. Thus our ARPES and calculation together suggest that the observed thermally driven topological phase transition is a result of thermal expansion of the lattice. This scenario is further supported by our x-ray diffraction measurements on the sample as a function of temperature. As shown in Fig. 4.10(c). We now compare the observation with the topological phase transition found in the Z2 TI system in BiTl(S1−δ Seδ )2 [37] shown in the previous chapter, in order to highlight interesting properties of the topological phase transition in Pb0.70 Sn0.30 Se. First, we observe that the momentum-space distance between the two Dirac points near each X̄ point in Pb0.70 Sn0.30 Se can be systematically engineered. We note that changing the surface Dirac point momentum space location is allowed in a mirror 108 4.3.2 Temperature-driven topological phase transition protected TCI system [117], as long as the Dirac points are on the mirror lines. This is, in contrast, not possible in BiTl(S1−δ Seδ )2 since it has only single Dirac cone at the surface BZ center (a time-reversal invariant Kramer’s point) as required by the timereversal protected TI phase. Second, at the topological phase transition critical point in Pb0.70 Sn0.30 Se, the two Dirac cones merge and also the bulk band-gap vanishes. Thus both the surface and the bulk possess Dirac dispersion, and the system can be viewed as a squared-version of graphene in three-dimension, potentially leading to exotic transport and tunneling behaviors awaiting to be explored [158]. Third, it is also interesting to note that similar temperature dependence study on BiTl(S0.4 Se0.6 ) does not show any dramatic temperature dependent effect. This is very likely due to the fact that Pb0.70 Sn0.30 Se is in the cubic crystal structure so there exists only one parameter a for the lattice constant. 4.3 TOPOLOGICAL SURFACE STATES IN PBδ SN1−δ SE Figure 4.10: Temperature-driven topological phase transition in Pb0.70 Sn0.30 Se. (a) Dispersion maps along the mirror line Γ̄− X̄− Γ̄ at different temperatures. The two Dirac points are observed to approach, eventually merge into one node and then open up a gap as temperature increases. (b) First-principles calculations of the TCI surface bands with varying lattice constants. SnSe assumed in the face-center cubic (FCC) structure is used. Red lines and blue areas represent the surface and bulk bands, respectively. (c) Synchrotronbased temperature dependent X-ray diffraction (SXRD) measurements for Pb0.70 Sn0.30 Se. The peak is observed to shifts towards the lower angles with increasing temperature, which confirms the picture of the thermal expansion of lattice (see supplementary information for details). (d) Surface Fermi surface plot measured at temperature of 20 K. This figure is adapted from Ref. [81]. 110 4.3.3 Topological phase diagram in Pb1−δ Snδ Se 4.3.3 Topological phase diagram in Pb1−δ Snδ Se We study the TCI phase in Pb1−δ Snδ Se as a function of composition δ. Fig. 4.11(a) shows the ARPES measurements of the low energy states of the δ = 0.3 sample, as well as the two end compounds, namely PbSe and SnSe. For PbSe, low-lying bulk conduction and valence bands with a clear band-gap of ∼ 0.15 eV is observed, which proves that the system is topologically trivial for δ = 0. As δ is increased, the lowlying bulk bands are observed to approach each other, and eventually inverse with the surface states spanning over the inverted band-gap. The band inversion critical composition is found to be 0.2 ∼ 0.23 depending on the temperature. We note that the fact that the increasing Sn concentration drives the system from trivial to TCI has also been found in the Pb1−δ Snδ Se (see previous section and also Ref. [40]). This is interesting since Pb is in fact heavier than Sn thus having a larger (atomic) spinorbit strength. However, in both Pb1−δ Snδ Se and Pb1−δ Snδ Te cases, shrinkage of the lattice constant (with increasing Sn%) plays a more important role and therefore makes the system topologically nontrivial on the Sn-rich side. We turn to the other end compound SnSe, as shown in the third panel in Fig. 4.11(a). Surprisingly, at the Fermi level, no electronic states are observed. On the other hand, a fully gapped electronic structure with the chemical potential inside the band-gap is found. This is because SnSe crystal is in the orthorhmobic phase [182, 183]. The change of crystal structure, which denies both the band inversion and the mirror symmetries, completely destroys the TCI phase. And SnSe is found to be a trivial insulator by our ARPES measurements and the band-gap is reported to be as large as ∼ 1 eV [184]. Based on our systematic ARPES studies, a rich topological phase diagram is found in the Pb1−δ Snδ Se in Fig. 4.11(b). The blue and red lines represent the energy level of the lowest lying bulk conduction and valence bands with assuming that the crystal structure always remains in the FCC structure. Starting from PbSe (δ = 0), the system has a non-inverted band-gap of ∼ 0.15 eV. As δ increases, band inversion takes 4.3 TOPOLOGICAL SURFACE STATES IN PBδ SN1−δ SE place and the system enters the TCI phase. the inverted band-gap increases until the system enters the multi-(crystal structure)-phase regime at δ & 0.45, where cubic and orthorhombic structures coexist. Finally, for δ & 0.75, the system becomes a large band-gap trivial insulator in the single orthorhombic phase. Two distinct phase transition are observed (as labeled by δc1 and δc2 ), where the first transition is due the the shrink of lattice constant (which increases the effective spin-orbit strength), whereas the second is a result of a drastic structural transition. Therefore, our experimental data reveal a delicate relationship among lattice constant, band gap, spin-orbit coupling strength and crystal structure associated with the topological phase transition in Pb1−δ Snδ Se. 112 4.3.3 Topological phase diagram in Pb1−δ Snδ Se Figure 4.11: Topological phase diagram Pb1−δ Snδ Se. (a) ARPES dispersion map for PbSe (trivial insulator), Pb0.7 Sn0.3 Se (TCI) and SnSe (trivial insulator). (b) Topological phase diagram of the Pb1−δ Snδ Se system. For composition range of 0 < x < 0.45, the system is in the single crystalline FCC phase. The bulk band of Pb1−δ Snδ Se undergoes a band inversion with Pb/Sn substitution. Topological crystalline insulator (TCI) phase is observed in the band inverted region toward the Sn-rich side. The critical composition δc1 is ∼ 0.20 − 0.23 depending on the temperature. The conduction and valence band states + representing odd and even parity eigenvalues are marked as L− 6 and L6 , respectively. For composition range of 0.45 < δ < 0.75, the system shows multi-structural-phase (cubic and orthorhombic phases coexist. See the XRD data in the inset for δ = 0.5 and 0.6.). The upper insets are schematic Fermi surface plots around the X̄ point. The inset in the bottom right conner shows the resistivity measurements on SnSe, which proves its insulator nature. BS FS and SS FS denote the bulk state Fermi surface and surface state Fermi surface, respectively. The arrows at bottom notes the compositions where our ARPES studies have been performed. For composition range of 0.75 < δ < 1, the system is in a single crystalline orthorhombic phase. This figure is adapted from Ref. [81]. Chapter 5 Topological Dirac semimetal state in Cd3As2 and Na3Bi Unlike insulators, semimetals are materials, whose bulk conduction and valence bands have small but finite overlap. Thus there does not exist a full band-gap irrespective of the choice of the chemical potential. This is in contrast to all topological phases discussed before this chapter (quantum Hall states, Chern insulators, quantum spin Hall insulators, 3D Z2 topological insulators, and topological crystalline insulators), where a band-gap is important both for the definition of a topological number and for the existence of surface states. We ask the following questions: Can we construct a topological state in a semimetal - a topological semimetal? What kind of surface states it will have and how these surface states reflect the nontrivial topology in the bulk of a semimetal? In this chapter, we present our experimental realization of a topological Dirac semimetal phase in Cd3 As2 and Na3 Bi. We show that the bulk has linearly dispersive nodal crossings, realizing a 3D analog of graphene, whereas the surface features Fermi arc surface states (FASS) that connect across the bulk Dirac nodes. Previously, Fermi arc states were only found in the bulk bands of high Tc cuprate superconductors in 114 a strongly interacting condition. Our observation of novel surface states here thus realizes disjoint Fermi arc states on the surface of a weakly interacting topological system. The observed FASS serve as a new type of 2D electronic gas, which are distinct from both a regular 2DEG in semiconductor heterostructures and the surface states in a topological insulator. The observed exotic surface and bulk electronic and spin groundstate in topological Dirac semimetals Cd3 As2 and Na3 Bi here suggests many interesting transport and tunneling phenomena, and is multiply-connected to other novel groundstates under additional superconducting or ferromagnetic symmetry breakings [10, 119–124, 139–141, 149, 185–192]. In the first section, we discuss the theoretical works that are directly relevant to the prediction the topological Dirac semimetal state. In the second section, we present our ARPES observation of the 3D Dirac cone state in the bulk electronic structure in Cd3 As2 . In the third section, we present our ARPES and spin-ARPES data on Na3 Bi, not only showing the existence of 3D Dirac nodes in the bulk, but also showing a spin-polarized double Fermi arc surface state (FASS) that connect the bulk Dirac nodes. We further demonstrate how the observed FASS and its spin texture provide an experimental measurement of the nontrivial topological number in semimetal Na3 Bi. Finally in the last section, we go back to theory. We discuss the general classification of topologically nontrivial semimetals, including the topological Weyl semimetal [119, 188], the topological Dirac semimetal [122–124] and the topological nodal-line semimetal [193], and how they can transform into each other via breaking or restoring certain symmetries. 5.1 THEORETICAL CONCEPTS FOR A TOPOLOGICAL DIRAC SEMIMETAL 5.1 Theoretical concepts for a topological Dirac semimetal In this section, we introduce the basic theoretical concepts relevant to the topological Dirac semimetal phase. We constrain ourselves within bulk materials that have time-reversal T and space inversion symmetries I, and possess non-negligible spinorbit coupling. These conditions are needed for a topological Dirac semimetal. For systems breaking T or I, and for spinless fermion systems (no spin-orbit coupling), there are also theoretically predicted distinct topological semimetal phases, such as a topological Weyl semimetal and a topological nodal-line semimetal. These phases have not been experimentally realized to date. In the last section of this chapter, we will briefly discuss them and their connection to a topological Dirac semimetal. In a time-reversal and space inversion symmetric system, if the energy of the top of a valence band goes above that of the bottom of a conduction band, without considering spin-orbit interaction, these two bulk band will become degenerate (bandcrossing) at a finite number of momentum space locations. However, a finite spinorbit interaction is expected to lift the degeneracy at these band-crossing momenta. Without considering any additional symmetry, there is no reason one would expect certain band-crossing momenta are more “special” than others. Therefore, if spinorbit coupling open an energy gap, it should opens an full energy gap, meaning the degeneracy at all band-crossing momenta are lifted. This is the case of the BiTl(S1−δ Seδ )2 and the Pb1−δ Snδ Te(Se) systems [37, 40] that we present in Chapters 3,4. However, the situation can become very different if additional symmetries are considered, in particular if we consider a time-reversal and space inversion symmetric system with an additional uniaxial rotational symmetry. Let us take the example of Na3 Bi, where a band inversion occurs between the Na3s and the Bi6p bands in the 116 vicinity of the Γ point. Due to an additional C3 rotational symmetry along the kz axis [Fig. 5.1(c)], the bulk electronic bands along the C3 (kz ) axis must be the eigenstates of the C3 operation. In particular for the Na3s and the Bi6p bands in Na3 Bi, theory [123] shows that these two bands have different C3 eigenvalues and therefore the bulk band degeneracy is protected by C3 crystalline rotational symmetry even with a finite spin-orbit coupling. Therefore, spin-orbit coupling opens an energy gap at all bandcrossing k-points except at two special momenta along the C3 (kz ) axis on opposite sides of the Γ point. Similarly, in another tetragonal structured material Cd3 As2 , it has been theoretically shown that the band-crossing between inverted conduction and valence bands is protected by an additional C4 rotational symmetry of the same reason [122]. A systematic theoretical classification for all the possible topological Dirac semimetal states with different rotational symmetries have been proposed in Ref. [124] [also see Fig. 5.2]. Another important theoretical question is to define a topological number to characterize a Dirac semimetal state. Let us again take the example of Na3 Bi, in absence of a full energy gap in the bulk BZ, one cannot define the Z2 invariants (ν0 ; ν1 ν2 ν3 ) as in a 3D Z2 topological insulator, even though there is a band inversion at the Γ point in Na3 Bi. However, as pointed out in Ref. [124], since the bulk band-gap only vanishes at two momenta along the C3 (kz ) axis on the opposite sides of the Γ point, there exist many 2D k planes in the 3D BZ, where a full energy gap is present. In particular, for Na3 Bi, the kz = 0 plane is invariant under time-reversal operation, and also contains the Γ point where the band inversion happens. Therefore, Ref. [124] shows that the kz = 0 plane can be viewed as a 2D quantum spin Hall system with a distinct 2D topological number ν2D (kz = 0) = 1. The approach of assigning topological numbers to certain 2D k slices in a 3D BZ can be further generalized to other Dirac semimetals (see Fig. 5.2 and Ref. [124]) and even Weyl semimetals [10,119,188]. Furthermore, the distinct 2D topological number (e.g. ν2D (kz = 0) = 1 in Na3 Bi) in a 5.1 THEORETICAL CONCEPTS FOR A TOPOLOGICAL DIRAC SEMIMETAL Dirac semimetal guarantees the existence of double Fermi arc surface states (FASS), as shown in Ref. [122–124]. About the FASS, we will elaborate in some detail in section 3 with our ARPES data on Na3 Bi. 118 Figure 5.1: Comparison of bulk band inversion transitions in time-reversal and inversion symmetric systems with or without additional symmetries. (a) A band inversion process in a time-reversal and inversion symmetric system without the influence of additional symmetries. In this case, as the conduction and valence bands are inverted, spinorbit coupling will open up a full energy gap. The BiTl(S1−δ Seδ )2 system [37] is an example. (b) The critical point of the band inversion realizes a 3D Dirac semimetal. Such 3D Dirac semimetal state requires fine tuning of the material composition δ. (c),(d) A band inversion process in a time-reversal and inversion symmetric system with an additional rotational symmetry. In this case, as the conduction and valence bands are inverted and cross each other, spin-orbit coupling will open up an energy gap everywhere in the k-space where they cross except at the momentum locations along the rotational axis. This is because the bulk band crossings on the rotational axis are protected by the rotational symmetry of the crystal. The groundstate in the inverted regime is described by a pair of Dirac nodes along the rotational axis in the bulk and double Fermi arc surface states connecting the two bulk nodes on the surface. Inset: an ARPES Fermi surface map of Na3 Bi showing the double FASS and the two bulk Dirac nodes. 5.1 THEORETICAL CONCEPTS FOR A TOPOLOGICAL DIRAC SEMIMETAL Figure 5.2: Classification table for 3D topological Dirac semimetals. This table is adapted from Ref. [124]. 120 5.2 3D Dirac semimetal state in high mobility Cd3As2 In this section, we present our ARPES results on the Dirac semimetal candidate Cd3 As2 . We observe a highly linear bulk band crossing to form a three-dimensional dispersive Dirac cone projected at the (001) surface BZ center by studying the (001)cleaved surface. These results demonstrate the existence of the 3D Dirac nodes (bandcrossing) in the bulk electronic structure of Cd3 As2 . Remarkably, an unusually inplane high Fermi velocity up to 1.5 × 106 m·s−1 is observed in our samples, where the transport mobility is known up to 40,000 cm2 V−1 s−1 [194,195] suggesting that Cd3 As2 can be a promising candidate as an anisotropic-hypercone (3D) high spin-orbit analog of graphene. Our observation of the 3D Dirac semimetal state in the stoichiometric, stable and high mobility material Cd3 As2 opens the door for exploring the exotic transport and tunneling phenomena based on 3D Dirac fermions [140, 141, 149, 186]. The crystal structure of Cd3 As2 has a tetragonal unit cell with a = 12.67 Å and c = 25.48 Å for Z = 32 with symmetry of space group I41 cd [see Figs. 5.3(a),(b)]. In this structure, arsenic ions are approximately cubic close-packed and Cd ions are tetrahedrally coordinated, which can be described in parallel to a fluorite structure of systematic Cd/As vacancies. There are four layers per unit and the missing CdAs4 tetrahedra are arranged without the central symmetry as shown with the (001) projection view in Fig. 5.3(b), with the two vacant sites being at diagonally opposite corners of a cube face [196]. The corresponding Brillouin zone (BZ) is shown in Fig. 5.3(d), where the center of the BZ is the Γ point, the centers of the top and bottom square surfaces are the Z points, and other high symmetry points are also noted. Cd3 As2 has attracted attention in electrical transport due to its high mobility of 105 cm2 V−1 s−1 reported in previous studies [194,195]. The carrier density and mobility of our Cd3 As2 samples are characterized to be of 5.2 × 1018 cm−3 and 42850 cm2 V−1 s−1 , respectively, at temperature of 130 K, consistent with previous reports [194, 195], which provide evidence for the high quality of our single crystalline samples. In band 5.2 3D DIRAC SEMIMETAL STATE IN HIGH MOBILITY CD3 AS2 theoretical calculations, Cd3 As2 is also of interest since it features an inverted band structure [197]. More interestingly, a very recent theoretical prediction [123] which motivated this work, has shown that the spin-orbit interaction in Cd3 As2 cannot open up a full energy gap between the inverted bulk conduction and valence bands due to the protection of an additional crystallographic symmetry [124] (in the case of Cd3 As2 it is the C4 rotational symmetry along the kz direction [123]), which is in contrast to other band-inverted systems such as Bi2 Se3 . This theory predicts [123] that the C4 rotational symmetry protects two bulk (3D) Dirac band touching points at two special k points along the Γ − Z momentum space cut-direction, as shown by the red crossings in Fig. 5.3(d). Therefore, Cd3 As2 serves as a candidate for a spacegroup or crystal structure symmetry protected C4 3D Dirac semimetal state. In order to experimentally identify such a 3D Dirac semimetal state, we systematically study the electronic structure of Cd3 As2 on the cleaved (001) surface. Fig. 5.3(c) shows momentum-integrated ARPES spectral intensity over a wide energy window. Sharp ARPES intensity peaks at binding energies of EB ≃ 11 eV and 41 eV that correspond to the cadmium 4d and the arsenic 3d core levels are observed, confirming the chemical composition of our samples. We study the overall electronic structure of the valence band. Fig. 5.3(e) shows the second derivative image of an ARPES dispersion map in a 3 eV binding energy window, where the dispersion of several valence bands are identified. Moreover, a low-lying small feature that crosses the Fermi level is observed. In order to resolve it, high-resolution ARPES dispersion measurements are performed in the close vicinity of the Fermi level as shown in Fig. 5.3(f). Remarkably, a linearly dispersive upper Dirac cone is observed at the surface BZ center Γ̄ point, whose Dirac node is found to locate at a binding energy of EB ≃ 0.2 eV. At the Fermi level, only the upper Dirac band, but no other electronic state, is are observed. On the other hand, the linearly dispersive lower Dirac cone is found to coexist with another parabolic bulk valence band, which can be seen from Fig. 5.3(e). From 122 the observed steep Dirac dispersion [Fig. 5.3(f)], we obtain a surprisingly high Fermi velocity of about 9.8 eV·Å (≃ 1.5 × 106 ms−1 ). Compared to the much-studied 2D Dirac systems, the Fermi velocity of the 3D Dirac fermions in Cd3 As2 is thus about 3 times higher than that of in the topological surface states (TSS) of Bi2 Se3 [32], 1.5 times higher than in graphene [198] and 30 times higher than that in the topological Kondo insulator phase in SmB6 [50]. The observed large Fermi velocity of the 3D Dirac band provides clues to understand Cd3 As2 ’s unusually high mobility reported in previous transport experiments [194,195]. Therefore one can expect to observe unusual magneto-electrical and quantum Hall transport properties under high magnetic field [140, 141, 149, 186]. It is well-known that in graphene the capability to prepare high quality and high mobility samples has enabled the experimental observations of many interesting phenomena that arises from its 2D Dirac fermions. The large Fermi velocity and high mobility in Cd3 As2 are among the important experimental criteria to explore the 3D relativistic physics in various Hall phenomena in tailored Cd3 As2 . We compare ARPES observations with our theoretical calculations, which is qualitatively consistent with previous calculations [123]. The reason for the use of our calculations is two fold: first, our calculations are fine tuned based on the characterization of samples used in the present ARPES study, second, sufficiently detailed cuts are not readily available from Ref. [123] which is necessary for a detailed comparison of ARPES data with theory. In theory, there are two 3D Dirac nodes that are expected at two special k points along the Γ − Z (kz ) momentum space cut-direction, as shown by the red crossings in Fig. 5.3(d). At the (001) surface, these two k points along the Γ − Z axis project on to the Γ̄ point of the (001) surface BZ [Fig. 5.3(d)]. Therefore, at the (001) surface, theory predicts one 3D Dirac cone at the BZ center Γ̄ point, as shown in [Fig. 5.4(a)]. These results are in qualitative agreement with our data, which supports our experimental observation of the 3D 3D Dirac semimetal state in Cd3 As2 . We also study the ARPES measured constant energy contour maps 5.2 3D DIRAC SEMIMETAL STATE IN HIGH MOBILITY CD3 AS2 [Fig. 5.4(c),(d)]. At the Fermi level, the constant energy contour consists of a single pocket centered at the Γ̄ point. With increasing binding energy, the size of the pocket decreases and eventually shrinks to a point (the 3D Dirac point) near EB ≃ 0.2 eV. A 3D Dirac semimetal is expected to feature nearly linear dispersion along all three momentum space directions close to the crossing point, even though the Fermi/Dirac velocity can vary significantly along different directions. In order to probe the 3D nature of the observed low-energy Dirac-like bands in Cd3 As2 , we performed ARPES measurements as a function of incident photon energy to study the out-of-plane dispersion perpendicular to the (001) surface. Upon varying the photon energy, one can effectively probe the electronic structure at different out-of-plane momentum kz values in a three-dimensional Brillouin zone and compare with band calculations. In Cd3 As2 , the electronic structure or band dispersions in the vicinity of its 3D Dirac2 (kz − k0 )2 = E 2 , where k0 is the like node can be approximated as : vk2 (kx2 + ky2 ) + v⊥ out-of-plane momentum value of the 3D Dirac point. Thus at a fixed kz value (which is determined by the incident photon energy value), do we have an in-plane electronic 2 (kz − k0 )2 . It can be seen that only dispersion takes the form: vk2 (kx2 + ky2 ) = E 2 − v⊥ at kz = k0 the in-plane dispersion that is a gapless Dirac cone, whereas in the case for kz 6= k0 the nonzero kz − k0 term acts as an effective mass term and opens up a gap in the in-plane dispersion relation. Fig. 5.5(a) shows the ARPES measured in-plane electronic dispersion at various photon energies. At a photon energy of 102 eV, a gapless Dirac-like cone is observed, which shows that photon energy hν = 102 eV corresponds to a kz value that is close to the out-of-plane momentum value of the 3D Dirac node k0 . As photon energy is changed away from 102 eV in either direction, the bulk conduction and valence bands are observed within experimental resolution to be separated along the energy axis and a gap opens in the in-plane dispersion. At photon energies sufficiently away from 102 eV, such as 90 eV or 114 eV in Fig. 5.5(a), the in-plane gap is large enough that the bottom of the upper Dirac cone (bulk con124 duction band) is moved above the Fermi level, and therefore only the lower Dirac cone is observed. We now fix the in-plane momenta at 0 and plot the ARPES data at kx = ky = 0 as a function of incident photon energy. As shown in Fig. 5.5(b), a E−kz dispersion is observed in the out-of-plane momentum space cut direction, which is in qualitative agreement with the theoretical calculations [Fig. 5.5(c)]. The Fermi velocity in the z-direction can be estimated (only at the order of magnitude level) to be about 105 m/s. These systematic incident photon energy dependent measurements show that the observed Dirac-like band disperses along both the in-plane and the out-of-plane directions suggesting its three-dimensional or bulk nature consistent with theory. In order to further understand the nature of the observed Dirac band, we study the spin polarization or spin texture properties of Cd3 As2 . As shown in Fig. 5.5(f), spinresolved ARPES measurements are performed on a relatively p−type sample. Two spin-resolved energy-dispersive curve (EDC) cuts are shown at momenta of ±0.1 Å−1 on the opposite sides of the Fermi surface. The obtained spin data shown in Figs. 5.5(g),(h) show no observable net spin polarization or texture behavior within our experimental resolution, which is in remarkable contrast with the clear spin texture in 2D Dirac fermions on the surfaces of topological insulators. The absence of spin texture in our observed Dirac fermion in Cd3 As2 bands is consistent with their bulk origin, which agrees with the theoretical prediction. It also provides a strong evidence that our ARPES signal is mainly due to the bulk Dirac bands on the surface of Cd3 As2 , whereas the predicted surface (resonance) states [123] that lie along the boundary of the bulk Dirac cone projection has a small spectral weight (intensity) contribution to the photoemission signal. In other words, according to our experimental data, the surface electronic structure of Cd3 As2 is dominated by the spin-degenerate bulk bands, which is very different from that of the 3D topological insulators. The distinct semimetal nature of Cd3 As2 is better understood from ARPES data 5.2 3D DIRAC SEMIMETAL STATE IN HIGH MOBILITY CD3 AS2 if we compare our results with that of the prototype TI, Bi2 Se3 . In Bi2 Se3 as shown in Fig. 5.5(b), the bulk conduction and valence bands are fully separated (gapped), and a linearly dispersive topological surface state is observed that connect across the bulk band-gap. In the case of Cd3 As2 [Fig. 5.6(a)], there does not exist a full bulk energy gap. On the other hand, the bulk conduction and valence bands “touch” (and only “touch”) at specific locations in the momentum space, which are the 3D band-touching nodes, thus realizing a 3D Dirac semimetal state. For comparison, we further show that a similar 3D Dirac semimetal state is also realized by tuning the chemical composition δ (effectively the spin-orbit coupling strength) to the critical point of a topological phase transition between a normal insulator and a topological insulator. Figs. 5.6(c)(d) present the surface electronic structure of two other 3D Dirac semimetal states in the BiTl(S1−δ Seδ )2 and (Bi1−δ Inδ )2 Se3 systems. In both systems, it has been shown that tuning the chemical composition δ can drive the system from a normal insulator state to a topological insulator state [37, 38, 75]. The critical compositions for the two topological phase transitions are approximately near δ = 0.5 and δ = 0.04, respectively. Fig. 5.6(c),(d) show the ARPES measured surface electronic structure of the critical compositions for both BiTl(S1−δ Seδ )2 and (Bi1−δ Inδ )2 Se3 systems, which are expected to exhibit the 3D Dirac semimetal state. Indeed, the bulk critical compositions where bulk and surface Dirac bands collapse also show Dirac cones with intensities filled inside the cones, which is qualitatively similar to the case in Cd3 As2 . Currently, the origin of the filling behavior is not fully understood irrespective of the bulk (out-of-plane dispersive behavior) nature of the overall band dispersion interpreted in connection to band calculations (see, Fig. 5.4). Based on the ARPES data in Figs. 5.6(c),(d), the Fermi velocity is estimated to be ∼ 4 eV·Å and ∼ 2 eV·Å for the 3D Dirac fermions in BiTl(S1−δ Seδ )2 and (Bi1−δ Inδ )2 Se3 , respectively, which is much lower than that of what we observe in Cd3 As2 , thus likely limiting the carrier mobility. The mobility is also limited by 126 the disorder due to strong chemical alloying. More importantly, the fine control of doping/alloying δ value and keeping the composition exactly at the bulk critical composition is difficult to achieve [37]. For example, although similarly high electron mobility on the order of 105 cm2 V−1 s−1 has been reported in the bulk states of Pb1−δ Snδ Se (δ = 0.23) [158], the bulk Dirac fermions there are in fact massive due to the difficulty of controlling the composition exactly at the critical point. These issues do not arise in the stoichiometric Cd3 As2 system since its 3D Dirac semimetal state is protected by the crystal symmetry, which does not require chemical doping and therefore the natural high electron mobility is retained (not diminished). We further note that Cd3 As2 is stable in ambient environment, whereas the other Dirac semimetal candidate Na3 Bi reacts in seconds in air. These advantages are vital in further studying the 3D Dirac electronic structure in transport. 5.2 3D DIRAC SEMIMETAL STATE IN HIGH MOBILITY CD3 AS2 Figure 5.3: Sample characterization on Cd3 As2 . (a) Cd3 As2 crystalizes in a tetragonal body center structure with space group of I41 cd, which has 32 number of formula units in the unit cell. The tetragonal structure has lattice constant of a = 12.670 Å, b = 12.670 Å, and c = 25.480 Å. (b) The basic structure unit is a 4 corner-sharing CdAs3 -trigonal pyramid. (c) Core-level spectroscopic measurement where Cd 4d and As 3d peaks are clearly observed. Inset shows a picture of the Cd3 As2 samples used for ARPES measurements. The flat and mirror-like surface indicates the high quality of our samples. (d) The bulk Brillouin zone (BZ) and the projected surface BZ along the (001) direction. The red crossings locate at (kx , ky , kz ) = (0, 0, 0.15 2π c∗ ) (c∗ = c/a). They denote the two special k points along the Γ − Z momentum space cut-direction, where 3D Dirac band-touchings are protected by the crystalline C4 symmetry along the kz axis. (e) Second derivative image of ARPES dispersion map of Cd3 As2 over the wider binding energy range. Various bands are wellresolved up to 3 eV binding energy range. (f ) ARPES EB − kx cut of Cd3 As2 near the Fermi level at around surface BZ center Γ̄ point. This figure is adapted from Ref. [43]. 128 Figure 5.4: Observation of in-plane dispersion in Cd3 As2 . (a) Left: First principles 2π calculation of the bulk electronic structure along the (π, π, 0.15 2π c∗ ) − (0, 0, 0.15 c∗ ) direction (c∗ = c/a). Right: Projected bulk band structure on to the (001) surface, where the shaded area shows the projection of the bulk bands. (b) ARPES measured dispersion map of Cd3 As2 , measured with photon energy of 22 eV and temperature of 15 K along the (−π, −π) − (0, 0) − (π, π) momentum space cut direction. (c) ARPES constant energy contour maps using photon energy of 22 eV on Cd3 As2 growth batch I. (d) ARPES constant energy contour maps using photon energy of 102 eV on Cd3 As2 batch II. In order to achieve chemical potential (carrier concentration) control, we have prepared different batches of samples under slightly different growth conditions (temperature and growth time). For the two batches studied here, batch I is found to be slightly more n−type than batch II (e.g. compare batch I in Fig. 5.3(f) with batch II in Fig. 5.5(a) rightmost panel). This figure is adapted from Ref. [43]. 5.2 3D DIRAC SEMIMETAL STATE IN HIGH MOBILITY CD3 AS2 Figure 5.5: Observation of out-of-plane dispersion in Cd3 As2 . (a) ARPES dispersion maps at various incident photon energies are shown in the first and third rows. First principle calculated in-plane electronic dispersion at different kz values near the 3D Dirac node k0 is plotted in the second and forth rows. (b) ARPES measured out-of-plane linear E − kz dispersion. (c) ARPES measured in-plane E − kx dispersion. The white dotted lines are guides to the eye tracking the out-of-plane dispersion. (d) Theoretically calculated out-of-plane E − kz dispersion near the 3D Dirac node shown over a wider energy window. (e) Schematic (cartoon) of the 3D (anisotropic) Dirac semimetal band structure in Cd3 As2 . (f ) Spin-integrated ARPES dispersion cut measured on the sample used for spin-resolved measurements. The dotted lines indicate the momentum locations for the spin-resolved EDC cuts. (g),(h) Spin-resolved ARPES intensity (black and red circles) and measured net spin polarization (blue dots) for Cuts 1 and 2. This figure is adapted from Ref. [43]. 130 Figure 5.6: Comparison of the surface electronic structure of 2D and 3D Dirac fermions. (a) ARPES measured surface electronic structure dispersion map of Cd3 As2 and its corresponding momentum distribution curves (MDCs). (b) ARPES measured surface dispersion map of the prototype TI Bi2 Se3 and its corresponding momentum distribution curves. Both spectra are measured with photon energy of 22 eV and at a sample temperature of 15 K. The black arrows show the ARPES intensity peaks in the MDC plots. (c),(d) ARPES spectra of two Bi-based 3D Dirac semimetals, which are realized by fine tuning the chemical composition to the critical point of a topological phase transition between a normal insulator and a TI: c, BiTl(S1−δ Seδ )2 (δ = 0.5), and (Bi1−δ Inδ )2 Se3 (δ = 0.04) (d). Spectrum in panel (c) is measured with photon energy of 16 eV and spectrum in panel (d) is measured with photon energy of 41 eV. For the 2D topological surface Dirac cone in Bi2 Se3 , a distinct in-plane (EB − kx ) dispersion is observed in ARPES, whereas for the 3D bulk Dirac cones in Cd3 As2 , TlBi(S0.5 Se0.5 )2 , and (Bi0.96 In0.04 )2 Se3 , a Dirac-cone-like intensity continuum is also observed. This figure is adapted from Ref. [43]. 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI 5.3 Fermi arc surface states in topological Dirac semimetal Na3Bi The topology of a topological phase is encoded in its surface states in experiments. The novel topological Dirac semimetal state has its bulk band-structure is similar to that of a three-dimensional analog of graphene. This is indeed observed in Cd3 As2 and Na3 Bi (see the previous section and also Ref. [43–45]). However, none of these experiments [43–45] revealed the signature of its topology in the Dirac semimetal state. In this section, we report the experimental discovery of a pair of polarized Fermi arc surface state modes in the form of a new type of two-dimensional polarized electron gas on the surfaces of Dirac semimetals. These Fermi arc surface states (FASS) are observed to connect across an even number of bulk band nodes and found to have their spin uniquely locked to their momentum. We show that these states are distinctly different from the topological surface states (TSS) seen in all topological insulators. Our observed exotic two-dimensional states not only uncover the novel topology of Dirac metals such as Na3 Bis but also opens new research frontiers for the utilization of Fermi arc electron gases for a wide range of fundamental physics and spintronic studies envisioned in recent theories [10, 119–124, 139–141, 149, 185–192]. 5.3.1 Choice of the surface termination to observe FASS We first elaborate the importance of choosing an appropariate surface termination in order to observe the Fermi arc surface states (FASS) in a topological Dirac semimetal candidate material. Let us take Na3 Bi as an example. Na3 Bi is a semimetal that crystalizes in the hexagonal P 63 /mmc crystal structure with a = 5.448 Å and c = 9.655 Å [199]. First principles bulk band calculations [123] show that its lowest bulk conduction and valence bands are composed of Bi 6px,y,z and Na 3s orbitals. These two bands possess a 132 5.3.1 Choice of the surface termination to observe FASS bulk band inversion of about ∼ 0.3 eV at the bulk BZ center Γ [123]. The strong spinorbit coupling in the system can open up energy gaps between the inverted bulk bands, but due to the protection of an additional three-fold rotational symmetry along the [001] crystalline direction, two bulk Dirac band-crossings (Dirac nodes) are predicted to be preserved even after considering spin-orbit coupling, as schematically shown by the blue crosses in Fig. 5.7(c). The two bulk Dirac nodes locate along the A-Γ-A [001] direction. Therefore, at the (001) surface, the two bulk Dirac nodes project onto the same point in the (001) surface BZ [Fig. 5.7(c)], making them difficult to separate, isolate, and systematically study via spectroscopic methods. More importantly, Fermi arc surface states are fundamentally not possible because a Fermi arc starts from one bulk Dirac node and ends on another (therefore requires multiple bulk Dirac nodes that are separated within the surface BZ). The situation in another topological Dirac semimetal candidate Cd3 As2 is almost identical [see Fig. 5.3(d)], where the two bulk Dirac nodes also locate on the [001] (kz ) axis. On the other hand, we note that previous ARPES experiments on Na3 Bi and Cd3 As2 [43–45] were performed on the (001) top surface, where the two Dirac nodes project onto the same point in the (001) surface BZ. Therefore, considering these facts, it is intuitive to understand why FASS were not observed in previous ARPES experiments [43–45]. On the other hand, at the (100) surface, the two bulk Dirac nodes are separated on the opposite sides of the (100) surface BZ center Γ̃ [Fig. 5.7(c)]. Consequently, the Fermi arc surface states that connect the bulk Dirac nodes are found in the (100) surface electronic structure calculation [Fig. 5.7(e)]. The surface states are double Fermi arcs because they exist everywhere on the Fermi surface contour except at the two bulk Dirac points. In other words, if one travels around the Fermi surface contour, the electronic states are localized at the surface everywhere, except at the locations of the two bulk Dirac points where the states disperse linearly in all three dimensions. We note that the existence of double Fermi arc surface states in Na3 Bi and cadmium 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI arsenide has been theoretically predicted by a number of groups [122–124,186], which strongly motivated our work to experimentally search for Fermi arc surface states in Dirac metals. Figure 5.7: Characterization of Na3 Bi system. (a) Crystal structure of Na3 Bi. The two Na sites and Bi atoms are marked with different colors. (b) Projected crystal structure at the (100) surface. (c) Structure of bulk and surface Brillouin zone at (001) and (100) surfaces. Bulk Dirac nodes are marked by blue crosses. Note that the two bulk Dirac cones project to the same Γ̄ point on the (001) surface, while they are separated in momentum when studied at the (100) surface. (d), (e), First principles calculation of the (001) (d) and (100) surface (e) electronic structure. Theoretical nontrivial surface state (green lines) appears along the edge of the bulk 3D Dirac cone in the (001) surface, while it becomes separated from the bulk continuum when seen from the (100) surface (e). (f ) First principles bulk band calculation for Na3 Bi. It is clear from the calculation that the band touching happens along the A-Γ-A direction close to the zone center. This figure is adapted from Ref. [46]. 134 5.3.2 Observation of Fermi arc surface states in Na3 Bi 5.3.2 Observation of Fermi arc surface states in Na3 Bi In order to observe the FASS and to illuminate the topological nature of the Dirac semimetal state in Na3 Bi, we systematically study the electronic and spin groundstate of its (100) surface-surface. Fig. 5.8(a) shows the ARPES measured Fermi surface of our Na3 Bi sample at its native Fermi level. Remarkably, the measured Fermi surface is found to consist of two Fermi “points” along the ky (100) direction and two arcs that connect the two Fermi points. The measured Fermi surface topology [Fig. 5.8(a)] is in agreement with the theoretical prediction [123], where two surface Fermi arcs connect the two bulk nodal touchings. In order to confirm that the observed Fermi surface is indeed the double Fermi arcs connecting two bulk nodal points, we study the evolution of constant energy contour as a function of binding energy EB . As shown in Fig. 5.8(b), the energy contour area of the two bulk nodal touching points is found to enlarge into contours as EB is increased (hole-like behavior), whereas the two surface Fermi arcs shrink while increasing EB (electron-like behavior). The evolution of the constant energy contour as a function of binding energy EB (electron or hole behavior for different bands) is also consistent with the theoretical expectation [see Fig. 5.8(d)]. To further confirm, we study the energy dispersion for important momentum space cut directions [Fig. 5.8(b)]. As shown in Fig. 5.8(c), surface states with a surface Dirac crossing are clearly observed near the Fermi level in Cut β, consistent with the theoretical calculation. The bulk valence band for Cut β is found to be away from the Fermi level. On the other hand, for Cuts α and γ, no surface states are observed but the bulk linear band is seen to cross the Fermi level, also consistent with the calculation [see Fig. 5.8(e)]. The contrasting behavior that for Cut β only surface states cross the Fermi level whereas for Cuts α and γ only the bulk linear bands cross the Fermi level serves as a piece of critical evidence for the existence of double Fermi arc surface states. We note that the two bulk nodal touchings observed in Fig. 5.8(a) still expand in a finite area in momentum space, rather than being ideal “points”. 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI This is because (1) electronic states in real samples have finite quasi-particle life time and mean free path, and (2) it is also possible that the chemical potential of our Na3 Bi sample is still slightly below the energy of the bulk nodes. In order to further confirm the 2D surface nature for the double Fermi arc surface states and the 3D bulk nature for the two bulk Dirac bands, we present Fermi surface maps at different incident photon energies. Upon varying the photon energy, one can study the electronic dispersion along the out-of-plane kz direction. Due to the different 2D vs 3D nature of the Fermi arc surface states and the bulk Dirac bands, the Fermi arc surface states are expected to be independent of kz (photon energy), whereas the bulk bands are expected to show strong kz dependence. As shown in Fig. 5.9(a), the double Fermi arcs are clearly observed irrespective of the choice of the photon energy values, which confirms their 2D surface nature. On the other hand, the two bulk nodal points are found to be quite pronounced at photon energies of 58 eV and 55 eV, but they become nearly unobservable as the photon energy is changed to 40 eV [e.g. the area highlighted by the red dotted circles in Fig. 5.9(a)]. This demonstrates the 3D bulk nature of the two bulk bands. To quantitatively evaluate how much the bulk band becomes weaker as hν is changed from 58 eV to 40 eV (its kz dependence), we denote the middle point of the left Fermi arc as “S” and the bottom bulk nodal touching point as “B” [Fig. 5.9(b)]. Fig. 5.9(c) shows the relative ARPES intensity between “S” and “B”. The strong dependence of I(B) I(S) upon varying photon energy shows that the bulk Dirac band becomes much weaker relative to the surface states as hν is changed from 58 eV to 40 eV, due to the reason that the kz value is moved away from the bulk nodal (Dirac) point. Furthermore, Fig. 5.9(d) shows the dispersion along Cut β, where the surface states with a clear Dirac crossing are observed at different photon energies. This confirms the 2D nature of the Fermi arc surface states along Cut β. In Fig. 5.9(e), we present photon energy dependent dispersion of the bulk nodal band [cut indicated by the white dotted line 136 5.3.2 Observation of Fermi arc surface states in Na3 Bi in Fig. 5.9(a)]. It can be seen that the bulk Dirac band only crosses the Fermi level at a photon energy around 58 eV and disperses strongly upon varying the photon energy (kz ) value, which confirms the 3D bulk nature of the bulk Dirac band. These systematic photon energy (kz ) dependent data, shown in Fig. 5.9, clearly demonstrate that the electronic states at the Fermi level are localized at the surface (2D surface state nature) everywhere around the Fermi surface contour, except at the locations of the two bulk nodal touching points, where the states disperse strongly in all three dimensions (3D bulk band nature). These data sets provide further support for the observation of double Fermi arc surface states in bismuth trisodium. We study the surface spin polarization along the Cut β. The white lines in Fig. 5.10(a) define the two momenta chosen for spin-resolved studies (namely S-Cut1 and S-Cut2). Spin-resolved measurements are performed at these two fixed momenta as a function of binding energy. Figs. 5.10(b),(c) show the in-plane spin-resolved intensity and net spin polarization. The magnitude of spin polarization reaches about 30% near the Fermi level. And the direction of spin polarization is reversed as one goes from S-Cut1 to S-Cut2, which shows the spin-momentum locking property and the singly degenerate nature of the Fermi arc surface states along the Cut β direction. 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI Figure 5.8: Observation of Fermi arc surface states. (a) A Fermi surface map of the Na3 Bi sample at photon energy of 55 eV. The BDP1 and BDP2 denote the two bulk Dirac points’ momentum space locations. Two surface Fermi arcs are observed to connect these two BDPs. (b) APRES constant energy contours as a function of binding energy at photon energy of 55 eV. The dotted lines note the momentum space cuts for Panel (c). (c) ARPES dispersion cuts α, β, γ as defined in Panel (b) at photon energy of 55 eV. Surface states for the Fermi arcs are observed in cut β, whereas the two bulk Dirac bands are seen in cuts α, γ. (d) Schematics of the constant energy contours drawn according to the theoretically calculated band structure. The red shaded areas and the orange lines represent the bulk and surface states, respectively. (e) Calculated band structure along Cut β and Cut α (γ). 138 5.3.2 Observation of Fermi arc surface states in Na3 Bi Figure 5.8: (f ) Structure of bulk and surface Brillouin zone at (001) and (100) surfaces. Bulk Dirac nodes are marked by blue crosses. Note that the two bulk Dirac cones project to the same Γ̄ point on the (001) surface, while they are separated in momentum space when studied at the (100) surface. The (100) surface was not studied in previous works due to the challenge of such cleavage in ARPES experiments (g) First principles bulk band calculation for Na3 Bi. (h) First principles calculation of the (100) surface electronic structure. This figure is adapted from Ref. [46]. Figure 5.9: Systematic studies on the double Fermi arc surface states. 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI Figure 5.9: Systematic studies on the double Fermi arc surface states. (a) ARPES Fermi surface maps at different photon energies. The double Fermi arcs are observed independent of the photon energy value, whereas the two bulk Dirac band points along ky become much weaker in intensity as the hν is changed from 58 eV to 40 eV, revealing their surface state and bulk band nature, respectively. (b),(c) In order to quantitatively evaluate how much the bulk band intensity gets weaker as hν is changed from 58 eV to 40 eV (its kz dependence), we denote the middle point of the left Fermi arc as “S” and the bottom bulk Dirac point as “B”. Panel (c) show the relative ARPES intensity between “S” and “B”. The strong dependence of I(B) I(S) upon varying photon energy shows the strong kz dependent nature the bulk band Dirac points. (d) ARPES dispersion maps of the surface states at two different photon energies. The surface states with a Dirac crossing are observed at both photon energies, which further supports its 2D nature. (e) ARPES dispersion maps of the bulk Dirac band at different photon energies [indicated by the white dotted lines in Panel (a)]. The bulk Dirac band only crosses the Fermi level for excitation photon energies around 58 eV, which demonstrates their three-dimensional dispersive (bulk) nature. This figure is adapted from Ref. [46]. Figure 5.10: Spin-momentum locking in double Fermi arc surface states. (a) The white dotted lines note the two momenta chosen for spin-resolved measurements. (b),(c) Spin-resolved ARPES intensity and net spin polarization along the in-plane tangential direction for S-Cuts1 and 2 at photon energy of 55 eV. Clear spin polarization and spinmomentum locking are found in the data, which demonstrate the singly degenerate nature of the Fermi arc surface states along the cut β k-space direction. This figure is adapted from Ref. [46]. 140 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi We use the obtained electronic and spin data for the (100) Fermi arc surface states to gain insights to the predicted 2D topological number (ν2D = 1) in bismuth trisodium. In Fig. 5.11, we present a series of ARPES dispersion maps. As schematically shown in Fig. 5.11(a), these maps, which are perpendicular to the k[001] axis, intersect with the axis at different k[001] values. As one goes from Slice1 to Slice7 along the k[001] axis, the ARPES measured and schematic energy dispersion for different sides are shown in Figs. 5.11(b),(c). Due to the existence of the two bulk nodes (Slices 2 and 6), the bulk band gap closes and reopens as one goes across each bulk node. Therefore, it is interesting to note that the k[001] axis serves as an effective axis for a bulk mass parameter in a 2D system. It is further interesting to note that the bulk band gap closings at Slices 2 and 6 correlated with the absence/appearance of the surface states at the Fermi level. As clearly seen in Figs. 5.11(b),(c), there are no surface states for Slice1. As one moves from Slice1 to Slice3, the bulk band gap closes and reopens, and surface states appear at the Fermi level of bismuth trisodium. Similarly, as one further goes from Slice3 to Slice7, the bulk band gap closes and reopens, and the surface states do not exists anymore for the data in Slice7. We note that the gap closing and reopening property that we observed here does not exist in the Fermi surface of any known topological insulator system such as Bi2 Se3 , which again highlights that the observed Fermi arc surface states (FASS) are different from the topological surface states (TSS) in a topological insulator. We focus on Slices 3-5, which are in-between the two bulk nodes. Interestingly, as seen in Figs. 5.11(b),(c), although surface states exist at the native Fermi level for any Slices that are in-between the two bulk nodes, they are in general gapped [e.g. Slice3 in Figs. 5.11(b)(c)]. The gapped nature of the surface states means that, for these Slices (k[001] 6= 0), there does not exist a nontrivial 2D topological number that can protect a doubly degenerate Dirac crossing for the surface states. This is intuitive 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI because these intermediate slices (k[001] 6= 0 and (k[001] 6= π) are not invariant under time-reversal symmetry (because time-reversal operation will translate kz to −kz ). Therefore, although the bulk bands are inverted, the two branches of the surface states can hybridize and open up an energy gap (Slice 3). However, for Slice4, which corresponds to k[001] = 0, the surface states are observed to be gapless with a surface Dirac point. Furthermore, our spin-resolved data in Fig. 5.10 clearly show that the two branches of the surface Dirac crossing carry opposite spin polarization. The gapless surface Dirac crossing and the spin-momentum locking for Slice4 (k[001] = 0), collectively, provide experimental evidence that the k[001] = 0 plane has a nontrivial 2D topological number, which is consistent with the ν2D = 1 for the time-reversal invariant k[001] = 0 slice predicted in theory [124]. After systematically studying the electronic structure of the Fermi arc surface states, we study the electronic structure of the two bulk Dirac cones. As shown in Figs. 5.8(b),(d) the two bulk nodes at the Fermi level expand into two contours as one goes to high binding energies (0≤EB ≤ 50 meV). Now we show the constant energy contour maps at even higher binding energies (EB ≥ 50 meV). As shown in Fig. 5.12(a), the two contours along the ky axis that correspond to the two bulk Dirac bands expand as one goes to higher binding energies. At the binding energy of ∼ 150 meV, the two separated Dirac band contours are found to just merge with each other. The merging of the two contours locates at two special momenta, (kx , ky ) −1 = (±0.15, 0) Å , which lead to the occurrence of saddle point singularity structure at these two special momenta. To directly identify the saddle point band structure as a result of the Lifshitz transition in experiments, we center our ARPES detector at one of the special momenta at (kx , ky ) = (+0.15, 0) Å −1 and study two E-k cuts. As shown in Fig. 5.12(b), the hybridized band reaches its local energy maximum at −1 (kx , ky ) = (+0.15, 0) Å along kx , while arriving a local energy minimum along ky . This behavior defines a saddle point singularity of band structure. In Fig. 5.12(c) 142 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi we compare and contrast the saddle point singularity electronic structure observed here with that observed in the surface states of a topological crystalline insulator Pb0.7 Sn0.3 Se. In the n-typed sample of Pb0.7 Sn0.3 Se, the two surface Dirac cones hybridizes at EB = 23 and 96 meV, signified also by saddle point singularities that are reported from ARPES as well as STM studies. The critical difference between these two cases is that for bismuth trisodium, bulk Dirac quasiparticles, instead of the surface Dirac electron gas in the case of TCI [81], merge and hybridize. Existence of singularities in the Dirac metals suggest that magnetic or superconducting dopants can potentially materialize correlated electron phenomena in these materials in future studies. The significance of the observation of Fermi arc surface states in metallic samples is analogous to the observation of Dirac surface states in 3D topological insulators [2, 6] since it is the boundary modes that carry the signature of a topological material [124, 186]). In fact, the topological property of Dirac semimetals was theoretically understood only very recently (see, Ref. [124, 186]), which took place after several numerical calculations and photoemission works showing that some of these materials possess bulk band structure that is analogous to 3D graphene [37, 43–45, 75, 122, 123]. It is theoretically shown that the most interesting or exotic physics of these materials are that of their surfaces not the bulk. Our observation of double Fermi arc surface states and their spin momentum locking demonstrates the topology of a Dirac semimetal. The observed surface states represent a new type of 2D electron gas, which is distinct from that of the surface states in a topological insulator. In a typical topological insulator such as Bi2 Se3 , the surface states’ Fermi surface is a closed contour. In sharp contrast, the Fermi surface in bismuth trisodium consists of two arcs, which are bridged by the two bulk nodes [Figs. 5.13(e),(f)]. Therefore, in this novel Fermi surface topology, as one goes along the surface Fermi arc and reaches a bulk node, the wavefunction of the surface state gradually loses its surface nature and 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI becomes a bulk band. Such exotic behavior, shown by our systematic ARPES data in Figs. 5.7-5.13, does not exist in surface states of Bi2 Se3 or any known topological insulators. This highlights the distinct topological nature of the nontrivial semimetal phase in a Dirac semimetal, which is fundamentally different from the known 3D TI phase [2, 6]. In surface electrical transport experiments at high magnetic field, it would be interesting to study how the surface electrons wind along the arc and enter the bulk singularity [186]. Moreover, if superconductivity can be induced by bulk doping in a Dirac semimetal, the surface state superconductivity can be topologically nontrivial, which could possibly lead to double Majorana-arc states [125,192]. Finally, the topological Dirac semimetal phase in a Dirac semimetal can be visualized as two copies of Weyl semimetals, where each bulk Dirac node is a composite of two degenerate Weyl nodes Fig. 5.13(e) that can be further split by additional symmetry breaking. There is no analogous picture for the surface states of strong topological insulators. At most, symmetry breaking in materials such as Bi2 Se3 will gap out the surface states. Additionally, our observation of multiple bulk nodal touching points realize a saddle point singularity in a strongly spin-orbit coupled material with linear dispersion in three-dimensions, which potentially paves the way for correlated electron physics [200, 201] with 3D Dirac or Weyl electrons. In conclusion, our systematic studies of bismuth trisodium surfaces have demonstrated a topological surface state analog for a 3D Dirac semimetal. The double surface Fermi arcs that we have observed connect the two bulk linear band touching points and exhibit spin polarization thus these results have identified the first topological phase in a Dirac semimetal, where the arc surface states and their unique spin momentum locking further evaluates a topological quantum number of ν2D = 1 for the k[001] = 0 2D (momentum slice) that uniquely defines the particular topological invariant realized in bismuth trisodium. Additionally, our data show that the two bulk linear bands exhibit a saddle point band structure, a form of singularity that can 144 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi induce electronic instability in Dirac fermions upon magnetic and superconducting doping of the metallic state in future studies. The observed Fermi arc surface states, which represent a new type of 2D electron gas, not only open the door for studying new fundamental physics phenomena, but also offer a new class of topological materials for further engineering into the nanoscience world [10,119–124,139–141,149,185–192]. 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI Figure 5.11: 2D topological number: Surface spin polarization and Momentumdependent band gap closing. (a) A schematic view of the band structure of the topological Dirac semimetal phase. Seven slices/cuts that are taken perpendicular to the k[001] axis are noted. (b),(c) ARPES measured [Panel (b)] and schematic [Panel (c)] band structure for these slices are shown. This figure is adapted from Ref. [46]. 146 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi Figure 5.12: Evolution through the bulk singularity. (a) ARPES constant energy maps obtained on the (100) surface. At EB = 50 meV and higher binding energies, the electronic states are mainly from the two bulk Dirac bands. The Constant energy contour at EB = 150 meV, where the two bulk disconnected (bulk) Dirac band contours just merge (the Lifshitz transition energy). (b) Dispersion of Cuts x and y, which are defined in Panel (c). The hybridization of the two bulk Dirac cones results in a saddle point singularity at the intersection of Cut X and Cut Y, signified by band maximum (lowest binding energy) along cut X and band minimum (highest binding energy) along cut Y. (c) Lifshitz transition of two bulk Dirac bands in bismuth trisodium with the Lifshitz transition of two surface Dirac bands in a topological crystalline insulator Pb0.7 Sn0.3 Se. 5.3 FERMI ARC SURFACE STATES IN TOPOLOGICAL DIRAC SEMIMETAL NA3 BI Figure 5.13: Comparison between the fine-tuning of a 3D Dirac semimetal and the topological Dirac semimetal. (a) A band inversion process in a time-reversal and inversion symmetric system without the influence of additional symmetries. In this case, as the conduction and valence bands are inverted, spin-orbit coupling will open up a full energy gap. The BiTl(S1−δ Seδ )2 system [37] is an example. (b) The critical point of the band inversion realizes a 3D Dirac semimetal. Such 3D Dirac semimetal state requires fine tuning of the material composition δ. (c),(d) A band inversion process in a time-reversal and inversion symmetric system with an additional rotational symmetry. In this case, as the conduction and valence bands are inverted and cross each other, spin-orbit coupling will open up an energy gap everywhere in the k-space where they cross except at the momentum locations along the rotational axis. This is because the bulk band crossings on the rotational axis are protected by the rotational symmetry of the crystal. 148 5.3.3 Topological invariant for the Dirac semimetal Na3 Bi Figure 5.13: The groundstate in the inverted regime is described by a pair of Dirac nodes along the rotational axis in the bulk and double Fermi arc surface states connecting the two bulk nodes on the surface. Inset: an ARPES Fermi surface map of Na3 Bi showing the double FASS and the two bulk Dirac nodes. (e),(f ) Schematic Fermi surface topology of bismuth trisodium and Bi2 Se3 . In bismuth trisodium, each Dirac node (the blue shaded area) can be viewed as a composite of two degenerate Weyl nodes (yellow and green areas). The orange arrows note the spin polarization according to our spin-resolved ARPES measurements. The inset of Panels (c),(e) shows the ARPES measured Fermi surface. This figure is adapted from Ref. [46]. 5.4 TOPOLOGICAL SEMIMETALS: DIRAC, WEYL, AND NODAL-LINE 5.4 Topological semimetals: Dirac, Weyl, and nodalline Now that we have presented the topological Dirac semimetal state and its double FASS using a concrete example of Na3 Bi, in this section we discuss different classes of topological semimetals. We note that topological semimetal is an actively ongoing research area both in experiments and in theories. The three classes (Dirac, Weyl, and nodal-line) listed here are the currently theoretically known ones (within band theory), but there might be other types being proposed in the future. We also note that our observation of 3D Dirac nodes and FASS in Na3 Bi is the first concrete realization of a topological Dirac semimetal (in the sense that the topological surface states (FASS) are observed). The other two classes, namely the topological Weyl semimetal [119, 188] and the topological nodal-line semimetal [193], remain completely experimentally elusive. Again, our discussion will only cover the concepts of these phases. While the detailed formulations can be found in theory papers [10,119,188,193], here the idea is to point out the key concepts that serve as important guidelines for us to experimentally search these new phases in real materials. Let us start from a Weyl semimetal. We have briefly mentioned the Weyl semimetal state in Chapter 3.1 (see Fig. 3.1). There we said that in a time-reversal invariant but space inversion symmetry breaking bulk material, as the system is tuned to go through a band inversion and a topological phase transition from a conventional band insulator to a topological insulator, there exists a range of tuning parameter δ values, where the band-gap goes to zero. Within this a range of tuning parameter δ values, the system is a Weyl semimetal. We note that the key is that in an inversion asymmetric system, the bulk electronic bands are singly degenerate except at the Kramers points. Therefore, as the bulk conduction and valence bands are inverted and cross each other, these crossings are between two singly degenerate bands. This is in sharp 150 contrast to the case in a Dirac semimetal (see the previous two sections for Cd3 As2 and Na3 Bi), where the crossings are between two doubly degenerate bands. For a band crossing between two singly degenerate bands, we can write down an effective Hamiltonian that describes the vicinity of the crossing point as H = ±v(px σx + py σy + pz σz ), (5.1) where ~p is the momentum from the crossing point, ~σ is the pseudo-spin. It can be immediately seen that this Hamiltonian satisfy the Weyl equation, and therefore the low-energy excitation of the bulk bands near the crossing is described by the Weyl equation. The ± sign here defines the “handness” or “chirality” of the (pseudo)spinmomentum locking. In theory, the “chirality” is also proportional to a “topological charge”, as one integrates the Berry’s phase around a Weyl point [10]. Now let us consider the simplest Weyl semimetal system where there are two Weyl nodes with the opposite “chiralities”, as shown in Fig. 5.14. This is a similar situation as in Na3 Bi (see Fig. 5.11) in the sense that there are only two points in the whole bulk BZ where the band-gap vanishes. Therefore, we consider the surface and bulk electronic structure on different 2D k-slices, similar to what we did in Fig. 5.11. As shown in Fig. 5.14, except at Slides 2 and 4, the bulk band structure has a full energy gap at all other 2D k-slices. Due to the existence of the Weyl nodes, the bulk bands go through two band inversions (gap closing and reopening) as one scans from Slide 1 to Slide 5. It is theoretically shown [10] that the 2D k-slide’s Chern number n changes by (±)1 as one crosses a Weyl point with the ± chirality. Therefore, in a Weyl semimetal, each k-slice (except the slices that contain the Weyl points where the system is gapless) can be treated as a 2D Chern insulator. This is shown in Fig. 5.14. Therefore, similar to a topological Dirac semimetal, a Weyl semimetal is described by a number of Weyl nodes in the bulk and Fermi arc surface states (FASS) connecting the Weyl nodes 5.4 TOPOLOGICAL SEMIMETALS: DIRAC, WEYL, AND NODAL-LINE on the surface. However, there is a key difference, which is the following: For an individual 2D k-slice that contains the FASS in a Weyl semimetal (e.g. see Slide 3 in Fig. 5.14), the surface state is a Chiral mode that is always gapless as long as the 2D k-slice cuts across the FASS (between Slides 2 and 4 in Fig. 5.14). On the other hand, for a topological Dirac semimetal, there is only one 2D k-slice (e.g. see Slide4 Fig. 5.11), where the FASS are gapless because they are protected by timereversal symmetry. In other words, the FASS in a Weyl semimetal share the same topological properties as the chiral edgestates in a Chern insulator, and such FASS are protected as long as lattice translational symmetry and the charge conservation (U(1) symmetry) hold. Whereas in a topological Dirac semimetal, besides translation and charge conservation, its FASS needs additional time-reversal or mirror symmetry to protect. Let us discuss the connection between a topological Weyl semimetal and a topological Dirac semimetal. It is well-known that each Dirac fermion can be viewed as a composite of two degenerate Weyl fermions with the opposite chiralities. Therefore, under time-reversal or space inversion symmetry breaking, a Dirac semimetal can be tuned into a Weyl semimetal. Let us again take the topological Dirac semimetal state in Na3 Bi as an example. Fig. 5.15 shows the evolution of the Na3 Bi groundstate as one breaks space inversion symmetry. It can be seen that each Dirac node splits into two Weyl nodes. And the system turns into a Weyl semimetal. It is interesting to see the surface states at different 2D k-slices, as there are in total 4 Weyl nodes, the Chern number changes its value 4 times. Additionally, since time-reversal symmetry is preserved, the 2D k-slice of kz = 0 is still protected by the time-reversal symmetry, and thus features a 2D Z2 topological number ν2D = 1. Similarly, one can figure out the evolution as one breaks time-reversal symmetry in Na3 Bi. Lastly, we briefly mention the topological nodal-line semimetal phase [193]. So far in Dirac and Weyl semimetals, the conduction and valence bands only cross each 152 other at discrete (0D) points in a bulk BZ. In a topological nodal-line semimetal, the band-crossing between the conduction and valence bands forms a 1D-closed-loop in a bulk BZ. And the surface states can be described as a “drum surface” whose boundary is the closed-loop of the bulk band crossing (see Fig. 5.16). Theoretically, such type of novel topological semimetal can be realized in a time-reversal and space-inversion symmetric spinless fermion bulk material, or a time-reversal or space-inversion breaking system with additional mirror symmetries. Since the experimental progress on these semimetals are preliminary, we do not go into further details. Nevertheless, it can be seen that topological semimetal is a truly exciting field. Realization of these new nontrivial semimetals can open a new era in topological insulator research. And breaking symmetries in the known topological Dirac semimetals Na3 Bi and Cd3 As2 is a promising route toward these new phases. 5.4 TOPOLOGICAL SEMIMETALS: DIRAC, WEYL, AND NODAL-LINE Figure 5.14: Electronic groundstate of a Weyl semimetal. Top: The Fermi surface of a Weyl semimetal is described by two Weyl nodes with opposite chiralities in the bulk and a FASS that connects the Weyl nodes on the surface. It has been theoretically shown that each k-slice (except the slices that contain the Weyl points where the system is gapless) can be viewed as a 2D Chern insulator. And as one scans across a ± Weyl point, the system’s Chern number changes by ±1. Bottom: Bulk and surface electronic dispersions on different 2D k-slices. 154 Figure 5.15: Tuning the Dirac semimetal Na3 Bi into a Weyl semimetal via space inversion symmetry breaking. Each Dirac node in Na3 Bi is a composite of two degenerate Weyl nodes with the opposite chiralities. Under inversion symmetry breaking, the Weyl nodes are separated in momentum space, realizing a Weyl semimetal. Figure 5.16: Bulk and surface electronic groundstate in a topological nodal-line semimetal. In a topological nodal-line semimetal, the conduction and valence bands are degenerate (cross each other) at a closed-1D-loop in a bulk BZ. And the surface states can be described as a “drum surface” whose boundary is the closed-loop of the bulk band crossing. This figure is adapted from Ref. [193]. Chapter 6 Topological states in 4f Kondo systems SmB6 and YbB6 Understanding the physics of strongly correlated systems is one of the most challenging tasks in physics. In solid states, strong electron-electron interaction is known to lead to many exotic groundstates ranging from Mott insulation, unconventional superconductivity, heavy fermion behavior, to a fractional quantum Hall state. Studying the interplay between nontrivial topology and strong correlation is of fundamental importance. In fact, the definition of a topological order (not a symmetry-protected topological state) intrinsically requires strong electron-electron interaction [24], and the only topological order realized in experiments to date is that of in a fractional quantum Hall state. Moreover, even within the framework of symmetry-protected topological states, introducing strong electronic correlation is also believed to dramatically enrich the possible topological classification as proposed recently [142, 202]. On the other hand, studying topological physics in a strongly correlated system is very challenging. Since the surface states in a strongly correlated system becomes non-electron-like quasi-particle excitations, currently there is no direct probe to systematically study the metallic surface modes including their energy-momentum dis156 persion and spin polarization, as what has been achieved via spin-ARPES in weakly interacting electronic systems. In this chapter, we present our ARPES studies on the surface and bulk electronic groundstate of certain Kondo systems with 4f electrons, in order to search for possible topologically nontrivial states in these correlated materials. The fact that we can still use ARPES to measure their surface states means that the correlation effects are not extremely strong so that band theory completely breaks down in all aspects in these systems. However, we show that electron interaction plays a vital role in the formation of the topological states and properties of the resulting surface states such as the surface Fermi velocity are quite different from a nearly non-interacting topological insulator such as Bi2 Se3 . Our study servers an important initial step toward realizing strongly correlated topological insulator states. The identification of topological surface states in 4f Kondo materials is particularly interesting due to a variety of symmetry breaking states such as heavy fermion superconductivity, ferromagnetism, antiferromagnetism, hidden order state, etc., which are known to occur in the rare-earth Kondo materials. 6.1 Observation of surface states in topological Kondo insulator candidate SmB6 Materials with strong electron correlations often exhibit exotic ground states such as the heavy fermion behavior, Mott or Kondo insulation and unconventional superconductivity. Kondo insulators are mostly realized in the rare-earth based compounds featuring f -electron degrees of freedom, which behave like a correlated metal at high temperatures whereas a bulk bandgap opens at low temperatures through the hybridization [203–205] of nearly localized-flat f bands with the d -derived dispersive conduction band. With the advent of topological insulators [2] the compound SmB6 , SERVATION OF SURFACE STATES IN TOPOLOGICAL KONDO INSULATOR CANDIDATE SMB6 often categorized as a heavy-fermion semiconductor [203–205], attracted much attention due to the proposal that it may possibly host a topological Kondo phase (TKI) at low temperatures where transport is anomalous [118, 206, 207]. The anomalous residual conductivity is believed to be associated with electronic states that lie within the Kondo gap [208–217]. Following the prediction of a TKI phase, there have been several surface-sensitive transport measurements, which include observation of a three-dimensional (3D) to two-dimensional (2D) crossover of the transport carriers below T ∼ 7K [106,107,218]. However, due to the lack of the critical momentum resolution for the transport probes, neither the existence of in-gap surface states nor their Fermi surface topology (number of surface Fermi surfaces and enclosing or not enclosing the Kramer’s points) have been experimentally studied. By combining high-resolution laser- and synchrotronbased angle-resolved photoemission techniques in Ref. [50], we present the surface electronic structure identifying the in-gap states that are strongly temperature dependent and disappear before approaching the coherent Kondo hybridization scale. Remarkably, the observed Fermi surface for the low-energy part of the in-gap states keeping the sample within the transport anomaly regime (T ∼ 6 K) reveals an odd number of pockets that enclose three out of the four Kramers’ points of the surface Brillouin zone, consistent with the theoretically calculated Fermi surface topology of the topological surface states. Concurrent ARPES studies on SmB6 are also reported in Refs. [49, 51]. SmB6 crystallizes in the CsCl-type structure with the Sm ions and the B6 octahedra being located at the corner and at the body center of the cubic lattice, respectively [Fig. 6.1(a)]. The bulk Brillouin zone (BZ) is a cube made up of six square faces. The center of the cube is the Γ point, whereas the centers of the square faces are the X points. Due to the inversion symmetry of the crystal, each X point and its diametrically opposite partner are completely equivalent. Therefore, there exist three distinct 158 X points in the BZ, labeled as X1 , X2 and X3 . It is well-established that the low energy physics in SmB6 is constituted of the non-dispersive Sm 4f band and the dispersive Sm 5d band located near the X points [106,211,212,218,219]. Figs. 6.1(d),(e) show ARPES intensity profiles over a wide binding energy scale measured with a synchrotron-based ARPES system using a photon energy of 26 eV. The dispersive features originate from the Sm 5d derived bands and a hybridization between the Sm 5d band and Sm 4f flat band is visible especially around 150 meV binding energies confirming the Kondo features of the electronic system in our study [Figs. 6.1(d),(e)]. In order to search for the predicted in-gap states within 5 meV of the Fermi level, a laser-based ARPES system providing ∆E ∼ 4 meV coupled with a low temperature (T ≃ 5 K) capability is employed in Ref. [50]. Since the low-energy physics including the Kondo hybridization process occurs near the three X points [Fig. 6.1(f)] in the bulk BZ and the X points project onto the X̄1 , X̄2 , and the Γ̄ points at (001) surface [Fig. 6.1(b)], the Kramers’ points of this lattice are X̄1 , X̄2 , Γ̄ and M̄ and one needs to systematically study the connectivity (winding) of the in-gap states around these points. Fig. 6.2(c) shows experimentally measured ARPES spectral intensity inte−1 grated in a narrow (±0.15 Å ) momentum window and their temperature evolution around the X̄ point. At temperatures above the hybridization scale, only one spectral intensity feature is observed around EB ∼ 12 meV in the ARPES EDC profile. As temperature decreases below 30 K, this feature is found to move to deeper binding energies away from the chemical potential, consistent with the opening of the Kondo hybridization gap while Fermi level is in the insulating gap (bulk is insulating, according to transport, so Fermi level must lie in-gap at 6 K). At lower temperatures, the gap value of hybridized states at this momentum space regime is estimated to be about 16 meV. More importantly, at a low temperature T ≃ 6 K corresponding to the 2D transport regime, a second spectral intensity feature is observed at the binding energy of EB ∼ 4 meV, which lies inside the insulating gap. Our data thus experi- SERVATION OF SURFACE STATES IN TOPOLOGICAL KONDO INSULATOR CANDIDATE SMB6 mentally shows the existence of in-gap states. Remarkably, the in-gap state feature is most pronounced at low temperature T ≃ 6 K in the 2D transport regime, but becomes suppressed and eventually vanishes as temperature is raised before reaching the onset for the Kondo lattice hybridization at 30 K. The in-gap states are found to be robust against thermal cycling, since lowering the temperature back down to 6K results in the similar spectra with the re-appearance of the in-gap state features [(Re 6K in Fig. 6.2(c)]. The observed robustness against thermal recyclings counts against the possibility of non-robust (trivial) or non-reproducible surface states. We further performed similar measurements of low-lying states focusing near the Γ̄ point (projection of the X3 ) as shown in Fig. 6.2(d). Similar spectra reveal in-gap state features prominently around EB ∼ 3 − 4 meV at T ≃ 6 K which clearly lie within the Kondo gap and exhibit similar (coupled) temperature evolution as seen in the spectra obtained near the X̄ point. We further study their momentum-resolved structure or the k-space map for investigations regarding their topology: 1) The number of surface state pockets that lie within the Kondo gap; 2) The momentum space locations of the pockets (whether enclosing or winding the Kramers’ points or not). Fig. 6.1(f) shows a Fermi surface map measured by setting the energy window to cover EF ± 4 meV, which ensures the inclusion of the in-gap states (that show temperature dependence consistent with coupling to the Kondo hybridization) within the Fermi surface mapping data as identified in Fig. 6.2(d),(e) at a temperature of 6 K inside the 2D transport anomaly regime under the “better than 5 meV and 7 K combined resolution condition”. Our Fermi surface mapping reveals multiple pockets which consist of an oval-shaped as well as nearly circular-shaped pockets around the X̄ and Γ̄ points, respectively. No pocket was seen around the M̄ -point which was measured in a synchrotron ARPES setting. Therefore the laser ARPES data captures all the pockets that exist while the bulk is insulating. This result is striking by itself from the point of view that while we know 160 from transport that the bulk is insulating, ARPES shows large Fermi surface pockets (metallicity of the surface) at this temperature. Another unusual aspect is that not all Kramers’ points are enclosed by the in-gap states. Our observed Fermi surface thus consists of 3 (or odd number Mod 2 around each Kramers’ point) pockets per Brilluoin zone and each of them wind around a Kramers’ point only and this number is odd (at least 3). Therefore, our measured in-(Kondo) gap states lead to a very specific form of the Fermi surface topology [Fig. 6.1(f)] that is remarkably consistent with the theoretically predicted topological surface state Fermi surface expected in the TKI groundstate phase despite the broad nature of the contours. Since for the laser-ARPES, the photon energy is fixed (7 eV) and the momentum √ window is rather limited (the momentum range is proportional to hν − W , where hν is the photon energy and W ≃ 4.5 eV is the work function), we utilize synchrotron based ARPES measurements to study the low-lying state as a function of photon energy as demonstrated in Bi-based topological insulators [2]. Figs. 6.2(e),(f) show the energy-momentum cuts measured with varying photon energies. Clear E − k dispersions are observed within a narrow energy window near the Fermi level. The dispersion is found to be unchanged upon varying photon energy, supporting their quasi-two-dimensional nature [see, Fig. 6.2(g)]. The observed quasi-two-dimensional character of the signal within 10 meV of the gap where surface states reside does suggest consistency with the surface nature of the in-gap states. Due to the combined effects of energy resolution (∆E ≥ 10 meV, even though the sample temperature, 7 K, is near the anomalous transport regime) and the intrinsic self-energy broadening coupled with the higher weight of the f -part of the cross-section and the strong band tails, the in-gap states are intermixed with the higher energy bulk bands’ tails. In order to isolate the in-gap states from the bulk band tails that have higher crosssection at synchrotron photon energies, it is necessary to have energy resolution (not just the low working temperature) better than half the Kondo gap scale which is about SERVATION OF SURFACE STATES IN TOPOLOGICAL KONDO INSULATOR CANDIDATE SMB6 7 meV or smaller in SmB6 . Our experiment reports of Fermi surface mapping covering the low-energy part of the in-gap states keeping the sample within the transport anomaly regime reveals an odd number of pockets that enclose three out of the four Kramers’ points of the surface Brillouin zone strongly suggesting a topological origin for the in-gap state. 162 Figure 6.1: Brillouin zone symmetry, and band structure of SmB6 . (a) Crystal structure of SmB6 . Sm ions and B6 octahedron are located at the corners and the center of the cubic lattice structure. (b) The bulk and surface Brillouin zones of SmB6 . High-symmetry points are marked. (c) Resistivity-temperature profile for samples used in ARPES measurements. (d), (e) Synchrotron-based ARPES dispersion maps along the M̄ − X̄ − M̄ and the X̄ − Γ̄− X̄ momentum-space cut-directions. Dispersive Sm 5d band and non-dispersive flat Sm 4f bands are observed, confirming the key ingredient for a heavy fermion Kondo system. (f ) A Fermi surface map of bulk insulating SmB6 using a 7 eV laser source at a sample temperature of ≃ 6 K (Resistivity= 5 mΩcm), obtained within the EF ± 4 meV window, which captured all the low energy states between 0 to 4 meV binding energies, where in-gap surface state’s spectral weight contribute most significantly within the insulating Kondo gap. Intensity contours around Γ̄ and X̄ reflect low-lying metallic states near the Fermi level, which is consistent with the theoretically predicted Fermi surface topology [207] of the topological surface states. This figure is adapted from Ref. [50]. SERVATION OF SURFACE STATES IN TOPOLOGICAL KONDO INSULATOR CANDIDATE SMB6 Figure 6.2: Temperature dependent in-gap states and its two-dimensional nature. (a) Cartoon sketch depicting the basics of Kondo lattice hybridization at temperatures above and below the hybridization gap opening. (b) Partially momentum-integrated −1 ARPES spectral intensity in a ±0.15 Å window (∆k defined in Panel (a)] above and below the Kondo lattice hybridization temperature [TH ). (c) Momentum-integrated ARPES spectral intensity centered at the X̄ point at various temperatures. 164 Figure 6.2: (d) Analogous measurements as in Panel (c) but centered at the Γ̄ pocket −1 (∆k = 0.3 Å ). ARPES data taken on the sample after thermally recycling (6 K up to 50 K then back to 6 K) is shown by Re 6K, which demonstrates that the in-gap states are robust against thermal recycling. (e) Synchrotron based ARPES energy momentum dispersion maps measured using different photon energies along the M̄ − X̄ − M̄ momentum space cut-direction. Incident photon energies used are noted on the plot. (f ) Momentum distribution curves (MDCs) of data shown in a. The peaks of the momentum distribution curves are marked by dashed lines near the Fermi level, which track the dispersion of the low-energy states. (g) Momentum distribution curves in the close vicinity of the Fermi level (covering the in-gap states near the gap edge) are shown as a function of photon energy which covers the kz range of 4π to 5π at 7 K. This figure is adapted from Ref. [50]. 6.2 TOPOLOGICAL SURFACE STATES IN YBB6 6.2 Topological surface states in YbB6 In a topological Kondo insulator (TKI), it is the Kondo hybridization between the d and f bands that leads to an inversion of the band parity and therefore realizes a topologically nontrivial insulator phase. A well-known example is the prediction of the TKI state in SmB6 [118, 207], and the following experimental works which identified the existence of in-gap surface states in SmB6 , consistent with the theoretically predicted TKI phase [49–52, 106, 107]. However, the surface states in TKI phase of SmB6 only exist at very low temperatures [50] and their Fermi velocity is expected to be low due to a strong f -orbital contribution [50, 207], limiting its future utilization in devices. In order to search for other novel correlated topological phases even without a Kondo mechnism, it is quite suggestive to systematically study the electronic groundstates of other rare-earth materials that are closely-related to SmB6 . SmB6 belongs to a class of materials called the rare-earth hexaborides, RB6 (R = rare-earth metal). In general, rare-earth hexaboride compounds are known to feature three types of electronic bands in the vicinity of the Fermi level, namely the the rare-earth 5d orbital band, the rare-earth 4f orbital band, and the boron 2p band. The low energy physics for a rare-earth hexaboride is collectively determined by the relative energies between these bands and the Fermi level, which depends on a delicate interplay among the key physical parameters including the valence of the rare-earth element, the lattice constant, the spin-orbit coupling (SOC), etc. Therefore, interestingly, the rare-earth hexaborides can realize a rich variety of distinct electronic ground states as seen in SmB6 , YbB6 , EuB6 and the superconducting state in LaB6 (Tc ∼ 0.5 K) [220, 221]. Motivated by these aspects, we study the surface and bulk electrnic structure of of another representative member of the rare-earth hexaboride family, ytterbium hexaboride (YbB6 ). Fig. 6.3 shows the theoretical calculated bulk band structure of both SmB6 and YbB6 . For SmB6 , calculation shows that a hybridization between the Sm 166 5d and Sm 4f bands near the Fermi level leads to a Kondo insulating gap, consistent with previous findings [207]. Interestingly, our calculation results [Figs. 6.3(a)-(c)] show that the groundstate is insensitive to the strength of the on-site coulomb repulsion U (qualitatively the same results for U = 0 and U = 8 eV), which demonstrates the robustness of the Kondo insulating state in SmB6 . In sharp contrast, in YbB6 , a Kondo insulating state is also seen without including coulomb repulsion [U = 0, see Fig. 6.3(d)]. However, as one increases the strength of the coulomb repulsion U, our calculation shows that the energy position of the Yb 4f bands are pushed to much higher energies below the chemical potential [Figs. 6.3(e),(f)], and therefore a Kondo insulating mechanism becomes irrelevant to the low energy physics.On the other hand, the B 2p bands become closer to the Fermi level and at certain intermediate U values [U = 5 eV, see Fig. 6.3(e)], an inversion between the Yb 5d and the B 2p bands is observed. This calculation suggests a novel scenario that a topological insulator state can be realized in the rare-earth hexaborides even without a Kondo insulating mechanism. In order to reveal the electronic state of YbB6 , we systematically study its electronic structure at the (001) natural cleavage surface. As shown in Fig. 6.4(c), the lowest 4f flat band in YbB6 is 1 eV below the Fermi energy. This is in sharp contrast to the ARPES data on SmB6 , where the flat 4f band is found to be only ≤ 15 meV away from the Fermi level [50]. Therefore, our data reveal the physical origin for the absence of the Kondo insulating state in YbB6 , which also negates the recent theoretical work that predicts the existence of the topological Kondo insulator phase in YbB6 [222]. Apart from the intense 4f band, our data in Fig. 6.4(c) also reveal an electron-like pocket centered at the X̄ point that crosses the Fermi level. In order to systematically resolve the Fermi level electronic structure, we present high-resolution ARPES measurements in the close vicinity of the Fermi level. It is important to note that at the studied (001) surface, the three X points (X1 , X2 , and 6.2 TOPOLOGICAL SURFACE STATES IN YBB6 X3 ) in the bulk BZ project onto the Γ̄ point and the two X̄ points on the (001) surface BZ, respectively. Since the valence band maximum and conduction band minimum are at the X-points, at the (001) surface one would expect low energy electronic states near the Γ̄ point and X̄ points. The Fermi surface map of YbB6 is presented in Fig. 6.4(a). Our Fermi surface map reveals multiple pockets, which consist of an oval-shaped contour and a nearly circular-shaped contour enclosing each X̄ and Γ̄ points, respectively. No pocket is seen around the M̄-point. YbB6 shows metallic behavior in transport [221] which is consistent with our data. We present ARPES energy and momentum dispersion maps, where low-energy states consistent with the observed Fermi surface topology are clearly identified. As shown in Fig. 6.4(b), a “V”-shaped nearly linearly dispersive band is observed at each Γ̄ and X̄ points. We further study the photon energy dependence of the observed “V”shaped bands. As shown in Figs. 6.4(b) and Figs. 6.5(a), the “V”-shaped bands are found to show no observable dispersion as the incident photon energy is varied, which suggests its quasi two-dimensional state nature. Therefore, our systematic ARPES data has identified three important properties in the YbB6 electronic structure: (1) A odd number of Fermi surface pockets are observed to enclose the Kramers’ point; (2) The bands at the Fermi level are found to exhibit nearly linearly (Dirac like) in-plane dispersion; (3) No observable out-of-plane (kz ) dispersion is observed for these Dirac like (“V”-shaped) bands. All these properties that we observed seem to suggest a possibility for a topological insulator state in YbB6 . Nevertheless, it is important to note that if these “V”-shaped bands are indeed the upper Dirac cone part of the topological surface states, then one would also expect the lower Dirac cone part and a well-defined Dirac crossing (the Dirac point of the surface states). In our data, some hole-like band [e.g. E ≃ −0.4 eV in the first panel of Figs. 6.5(a)] is seen that can correspond to the low Dirac cone. The observed hole-like band features are not sharp enough to draw any definitive conclusion for a clear Dirac crossing. We further test 168 the temperature dependence of these “V”-shaped bands. As shown in Fig. 6.5(b), the “V”-shaped bands are observed to be quite robust as one increases temperature. Finally, in order to confirm that what observed in ARPES is indeed the topological surface states, we perform First-principles slab calculation of the (001) surface with U = 4 eV as shown in Fig. 6.6. Dirac-cone surface states are clearly seen in the bulk energy-gap at the Γ̄ and the X̄ points, both of which correspond to the projection of the X points in the bulk BZ. Taken the ARPES and the calculation results collectively, we have demonstrated the topological surface states in YbB6 and further shown that the topological insulator state in YbB6 is irrelevant to a Kondo insulating gap since the lowest 4f flat band in YbB6 is 1 eV below the Fermi energy. Therefore, our studies of the surface and bulk electronic structure in YbB6 present a novel scenario that a topological insulator state is realized in YbB6 due to d − p hybridization without a Kondo insulating mechanism. 6.2 TOPOLOGICAL SURFACE STATES IN YBB6 Figure 6.3: Bulk band structure (GGA+U) calculation of Sm6 and YbB6 . (a), (b) Band structure of SmB6 from GGA calculations. Sizes of yellow, blue, and green dots denote weights of Sm-4f , Sm-5d, and B-2p orbitals in various bands. Zoomed in view in Pane (b). (c) Low-energy band structure around EF based on GGA and GGA+U (U = 8 eV) computations. (d)-(f ) Band structure calculation of YbB6 at various U values. Top: large energy range. Middle: Zoomed-in view. Bottom: Scematic. 170 Figure 6.4: Topological surface states in YbB6 . (a) ARPES measured Fermi surface of YbB6 . Circular shaped pockets are observed at Γ̄ and X̄ points. This spectrum is measured with photon energy of 50 eV at temperature of 15 K. (b) ARPES dispersion maps measured with different photon energy. (c) ARPES measured dispersion maps along the Γ̄ − X̄ − Γ̄ momentum-space cut-directions. Dispersive cone like pocket and non-dispersive flat Yb 4f bands are observed. The measured photon energy are noted on the plots. This figure is adapted from Ref. [86]. 6.2 TOPOLOGICAL SURFACE STATES IN YBB6 Figure 6.5: Photon energy and temperature dependent dispersion maps. (a) Photon energy dependent dispersion map with wider binding energy. The measured photon energy are noted on the plots. The 4f flat bands are about 1 eV below the Fermi level. These spectra are measured along the Γ̄ − X̄ momentum space cut direction with temperature of 15K . (b) Temperature dependent ARPES spectra. The measured temperature are noted on the plots. The slight variation of the pocket with temperature is likely due to the thermal expansion of the sample. These spectra are measured along the Γ̄ − M̄ momentum space cut direction. This figure is adapted from Ref. [86]. 172 Figure 6.6: Theoretical calculation showing the topological surface states on the (001) surface of YbB6 . First-principles slab calculation of the (001) surface with U = 4 eV. Dirac-cone surface states are clearly seen in the bulk energy-gap at the Γ̄ and the X̄ points, both of which correspond to the projection of the X points in the bulk BZ. Chapter 7 A route to 2D topological superconductivity The interplay between a topological insulator state and a symmetry-breaking (superconducting or ferromagnetic) state is of interest in both fundamental physics and applications [2, 6, 9, 53–61, 125–128, 223–226]. Specifically, inducing superconductivity in the Dirac surface states of a topological insulator is believed to realize Majorana fermion excitation [125] and supersymmetry phenomenon [128] in a condensed matter setting. A Majorana fermion is a non-Abelian quasi-particle, which is believed to be the key building block of a topological quantum computer. Supersymmetry is a fascinating high energy physics concept, which remains elusive in particle physics experiment to date. On the other hand, a ferromagnetically ordered topological insulator can realize a Chern insulator in its 2D thin film geometry [127], which means that the boundary of the 2D film will host chiral electronic edge-modes with a quantized Hall conductance even without an external magnetic field. This is of much interest in building low-power electronics. Furthermore, a magnetic topological insulator is predicted to show quantized Kerr rotation [126, 223], which serves as an independent measure of the topological number besides the spin-ARPES measurements on the 174 topological surface states. The same effect is also theoretically known to simulate the electrodynamics of the Axion [224], a particle candidate for the dark matter. Despite the interest, none of the major TI materials (such as Bi2 Se3 ) are natural superconductors or ferromagnets. Therefore, one has to dope a TI material or interface with a superconductor or ferromagnet, in order to induce these symmetry breaking-states. In this chapter, we present our systematic ARPES and spin-ARPES measurements on magnetically doped TIs and heteostructure samples between a TI thin film and an s-wave superconductor. Since ARPES is a probe that measures the electronic quasiparticle spectrum without nanometer spatial resolution, thus it is not practically possible to directly measure the Majorana exciations (non-electron quasi-pariticles) in a superconducting TI or the chiral edge states (a 1D state) in a magnetically doped TI thin film. The goal of our experiments is to experimentally demonstrate the electronic and spin groundstates that are required for these theoretically proposed phenomena. 7.1 Hedgehog spin texture in a magnetic topological insulator Understanding and control of spin degrees of freedom on the surfaces of topological materials are the key to future applications as well as for realizing novel physics such as the axion electrodynamics associated with time-reversal symmetry breaking on the surface. We experimentally demonstrate the momentum space spin texture in Bi2 Se3 surface states, where a surface band-gap is observed to open due to magnetic Mn doping. The resulting electronic and spin groundstate on the surface of Mn-doped Bi2 Se3 exhibits unique hedgehog-like spin textures at low energies which directly demonstrates the mechanics of time-reversal symmetry breaking on the surface. We further show that an insulating gap induced by quantum tunneling between surfaces 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR exhibits spin texture modulation at low energies but respects time-reversal invariance. These spin phenomena and the control of their Fermi surface geometrical phase first demonstrated in our experiments pave the way for future realization of many predicted exotic magnetic phenomena of topological origin. Interplay between ferromagnetism and the Z2 topological insulator state is believed to give rise to novel physics, such as a quantum anomalous Hall state [127] and the topological magneto-optic effect [126]. These phenomena rely on breaking timereversal symmetry in a topological insulator. It is known that the a gap at the Dirac point will open in the surface states as time-reversal symmetry is breaking. However, a surface band-gap can also open due to other mechanisms such as the tunneling between the top and bottom surfaces as a TI becomes thin. Here we use spin-ARPES to measure the momentum space spin texture of gapped surface states in Bi2 Se3 samples, where the Dirac point gap is opened by two distinct ways, namely doping magnetic (Mn) impurities or reducing the thickness of the Bi2 Se3 sample. We show that the spin texture near the edge of the surface gap behavior distinctly different in these two cases due to the different gap opening mechanisms. In particular, we show that Mndoping in Bi2 Se3 leads to a unique hedgehog-like spin texture at low energies near the edge of the magnetic gap, which directly demonstrates the mechanics of time-reversal symmetry breaking on the surface. The spin-resolved measurements demonstrated here can be utilized to probe quantum magnetism on the surfaces of other materials as well. In order to study the evolution of topological surface states upon magnetic doping, magnetically (Mn%) and (chemically similar) non-magnetically (Zn%) doped Bi2 Se3 thin films are prepared in high quality using the molecular beam epitaxy (MBE) growth method. A sample layout and a photograph image of a representative MBE grown film used for experiments are shown in Figs. 7.1(a),(b). Using standard Xray magnetic circular dichroism [227, 228], we characterize the magnetic properties of 176 doped Bi2 Se3 films [Figs. 7.1(c)]. In Mn-doped Bi2 Se3 , a hysteretic behavior in the out-of-plane magnetic response is observed consistently which suggests a ferromagnetically ordered groundstate. The observation of ferromagnetic character and its absence in Zn-Bi2 Se3 motivate us to systematically compare and contrast the electronic density of state behavior in the vicinity of the surface Dirac node of these samples. Fig. 7.1(d) shows the measured electronic states of Mn(Zn)-doped Bi2 Se3 using highresolution (spin-integrated) angle-resolved photoemission spectroscopy (ARPES). In the undoped Bi2 Se3 film [leftmost panel of Fig. 7.1(d)], a map of spectral density of states reveals a bright and intact Dirac node (signaled by the red spot located at the Dirac crossing in the panel), which indicates that in undoped Bi2 Se3 the Dirac node is gapless, consistent with the previous studies of pure Bi2 Se3 [32]. In samples where Mn atoms are doped into the bulk [first row Fig. 7.1(d)], we observe that the corresponding bright (red) spot at the Dirac node gradually disappears, revealing a clear systematic spectral weight suppression (SWS) with increasing Mn concentration. In contrast, the spectral intensity at the Dirac node is observed to survive upon systematic Zn doping except for the Zn=10% sample where some suppression of intensity is observed. This suggests that the Dirac node remains largely intact upon Zn doping. The observed systematic behavior of spectral evolution motivates us to quantitatively define an energy scale, ESWS , associated with the SWS observed at the Dirac node. The ESWS is taken as the energy spacing between the upper Dirac band minimum and the Dirac node location along the energy axis as illustrated in Fig. 7.1(e), which roughly corresponds to half of the surface gap magnitude. The value of the energy scale can be quantitatively determined by fitting the ARPES measured energy-momentum distribution curves. The doping dependence of the ESWS on samples measured at T = 20 K is shown in Fig. 7.2(c). The ESWS is observed to increase rapidly with Mn concentration but it remains nearly zero with Zn doping. The effect of temperature dependence on ESWS is shown in Fig. 7.2(d). The temper- 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR ature induced decrease of ESWS is consistent with gradual weakening of magnetism. These observations collectively reveal direct correlation between X-ray magnetic circular dichroism measured ferromagnetic character and the ARPES measured SWS (or gap) on the Mn-Bi2 Se3 films. Although the predominant trend in the doping evolution of surface states suggests a correlation between magnetism and SWS, we do notice a non-negligible ESWS at high Zn concentration (10%). This is likely due to increasing chemical disorder on the surface of the film since disorder degrades the surface quality. Similarly, magnetization measurements show that ferromagnetism vanishes before reaching T = 300 K [inset of Fig. 7.2(b)], but nonzero SWS [Fig. 7.2(d)] is still observed perhaps, in this case, due to thermal disorder of the relaxed film surface at high temperatures. Therefore, the correlation between ferromagnetism and the ARPES gap is only clear at low temperatures in samples with reduced disorder. The momentum width (∆k) of the surface electronic states can be taken as a rough relative measure of surface disorder, sample to sample, which is found to significantly increase upon both magnetic and non-magnetic dopings [Fig. 7.2(c)]. Strong spatial fluctuations of the surface electronic states in doped Bi2 Se3 has been observed in a recent STM work by Beidenkopf et al. [93], where the authors suggest the observation of gap-like feature at the Dirac point without breaking TR symmetry. These ambiguities associated with the observed gap-like feature across many different experiments strongly call for critically important spin-resolved measurements which also serve as a collective method, as we show, to unambiguously identify the correct nature of the gap. In order to study the evolution of spin texture upon magnetic doping, we perform spin-resolved measurements on Mn-Bi2 Se3 topological surface states. We present two independent but representative spin-resolved ARPES measurements on Mn(2.5%)Bi2 Se3 film I and film II. Films I and II, both containing same nominal Mn concentration, are measured and analyzed using two different spectroscopic modes, namely, 178 spin-resolved momentum distribution curve (spin-resolved MDC) measurement mode and spin-resolved energy distribution curve (spin-resolved EDC) measurement mode, in order to exclude any potential systematic error in the spin measurements. Figs. 7.3(a)(d) show measurements on film I. Our data shows that out-of-plane spin polarization Pz is nearly zero at large momentum k// far away from the Dirac point energy [0 < EB < 0.1 eV in Figs. 7.3(c), (d)]. While approaching the Dirac point (0.1 eV< EB < 0.3 eV), an imbalance between the spin-resolved intensity in +ẑ and −ẑ is observed [Fig. 7.3(c)]. The imbalance is found to become systematically more pronounced in the data set where scans are taken by lowering the energy toward the Dirac point. This systematic behavior observed in the data reveals a net significant out-of-plane spin polarization in the vicinity of the “gapped” Dirac point or near the bottom of the surface state conduction band. More importantly, the out-of-plane spin component Pz does not reverse its sign in traversing from −k// to +k// . Such behavior is in sharp contrast to the spin textures observed in pure Bi2 Se3 [34] where spins point to opposite directions on opposite sides of the Fermi surface as expected from TR symmetry. Therefore, our Pz measurements on film I near the gap edge reveal the TR breaking nature of the Mn-Bi2 Se3 sample where magnetic hysteresis was observed using X-ray magnetic circular dichroism technique. In order to directly measure the spin of the surface state at Γ̄ (the Kramers’ momentum, k// = 0), we perform spin measurements on Mn-Bi2 Se3 film II (same Mn concentration as film I) working in the spin-resolved EDC mode. The measured out-of-plane spin polarization (Pz ) is shown in Fig. 7.3(g). We focus on the Pz measurement at Γ̄, the Kramers’ momentum k// = 0 (red curve): the surface electrons at TR invariant Γ̄ are clearly observed to be spin polarized in the out-of-plane direction. The opposite sign of Pz for the upper and lower Dirac band [red curve in Fig. 7.3(g)] shows that the Dirac point spin degeneracy is indeed lifted up (E(k// = 0, ↑)6=E(k// = 0, ↓)). Such observation directly counters the Kramers’ theorem and therefore manifestly breaks the TR sym- 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR metry on the surface. Next we analyze Pz measurements at finite k// [green curves in Fig. 7.3(g)] to extract the detailed configuration of the spin texture. In going to larger k// away from the Γ̄ momenta, the measured Pz is found to gradually decrease to zero. Moreover, the constant energy momentum space plane at the Dirac point (EB = ED ) is observed to serve as a mirror plane that reflects all of the out-of-plane spin components between the upper and lower Dirac bands. Thus both spin-resolved MDC (film I) and spin-resolved EDC (film II) measurement modes result in the consistent conclusions regarding the spin configuration of the films. These systematic measurements, especially at the vicinity of the gap, reveal a hedgehog-like spin configuration for each upper(or lower) Dirac band separated by the magnetic gap, which breaks TR symmetry, as schematically presented in the inset of Fig. 7.3(f). Spin texture measurements on non-magnetically doped films Zn(1.5%)-Bi2 Se3 are presented in Figs. 7.4(a)-(d). The out-of-plane polarization Pz measurements reveal a sharp contrast to the magnetically doped Mn-Bi2 Se3 films, specifically, the near absence of finite Pz component around Γ̄ within our experimental resolution [Fig. 7.4(d)]. A very small Pz , however, at large k// is observed, which is expected due to surface state warping also observed in other topological insulator (TI) compounds [229] [Fig. 7.4(d)]. The signal being associated with warping is further confirmed in our data due to their TR symmetric nature, that Pz is observed to reverse its sign in traversing from −k// to +k// . Moreover, our in-plane spin measurements [Fig. 7.4(c)] show that Zn-Bi2 Se3 film retains the helical spin texture protected by the TR symmetry, as observed in pure Bi2 Se3 and Bi2 Te3 single crystals [34]. Therefore we conclude that nonmagnetic Zn doping does not induce observable spin reorientation on the topological surface. The contrasting behavior observed between Mn-Bi2 Se3 and ZnBi2 Se3 samples as presented in Figs. 7.3, 7.4 provide clear evidence for TR symmetry breaking in Mn-Bi2 Se3 . A surface band gap at the Dirac point can also be generated in Bi2 Se3 in its 180 ultra-thin film limit. In this case, the top and bottom surfaces couple together and open up a gap as electrons can tunnel from one to the other [Figs. 7.4(e)-(h)]. Such a gap in the surfaces is not related to magnetism. It is important to know the spin configuration associated with such a gap. In Figs. 7.4(e)-(h), we utilize Spin-resolved ARPES to measure the spin configuration on the very top region (within 5 Å) of a Bi2 Se3 film whose thickness is three quintuple layers (3 QL≃ 28.6Å). At large −1 parallel-momenta far away from Γ̄ [e.g. -0.10 Å in Fig. 7.4(g)], we observe clear spin polarization following left-handed helical configuration with the magnitude of the polarization around 35 − 40%. However, in going to smaller k// , the magnitude of the spin polarization is observed to be reduced. At the TR invariant Γ̄ momenta, spin-resolved measurements [Fig. 7.4(g) red curve] show no net spin polarization. This reduction of the spin polarization at small momenta near the gap is an intrinsic effect. These observations can be understood by considering the scenario where the surfaceto-surface coupling dominates, and the two energetically degenerate surface states from top and bottom that possess opposite helicities of the spin texture cancel each other at Γ̄ [62]. This results in strong suppression of spin polarization in the vicinity of this gap, whereas upon probing momenta to large k// away from Γ̄, the finite kinetic energy of the surface states (∝vk// ) naturally leads to the spatial decoupling of two Dirac cones. These spin measurements on the ultra-thin Bi2 Se3 film reveal the interplay between quantum tunneling (coupling) and the spin texture modification, which is of importance in spin-based device design with thin films. The observed spin texture however does not break TR symmetry, since the spins remain doubly degenerate at the TR invariant momenta Γ̄. This is in clear contrast to the spin texture observed in Mn-Bi2 Se3 . The magnetic contribution to the gap of the Mn-Bi2 Se3 film can be quantitatively identified using the spin texture data. The simplest k·p Hamiltonian that describes topological surface states under TR symmetry breaking can be written as 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR H = v(kx σy − ky σx ) + bz σz , where σ and k are the spin and momentum operators respectively, bz corresponds to half of the magnetic gap and v is the velocity of the surface Dirac band. We specify the out-of-plane polar angle θ of the spin polarization vector [inset of Fig. 7.3(g)] as θ = arctan PP//z . The magnitude of the polar angle θ reflects the competition between the out-of-plane TR breaking texture (∝bz ) and the in-plane helical configuration component (∝vk// ). Using the measured spin-resolved data sets (θ, k), we fit the magnetic interaction strength bz within a k·p scenario. As an example, we fit bz based on spin-resolved data sets in Fig. 7.3(g) on Mn(2.5%)Bi2 Se3 film II, as shown in Fig. 7.5(c) and obtain a value of 21 meV. This is a significant fraction of the SWS energy scale observed on the same sample, ESWS > 50 meV (see Fig. 7.2(c) for Mn=2.5%) obtained from the spin-integrated measurements in Fig. 7.1(c). Thus we identify the magnitude of the magnetic contribution (bz ) to the observed spectral weight suppression using spin-sensitive measurements, which suggests that the magnetic contribution is significant to ESWS . As demonstrated recently [37], the geometrical phase (GP) defined on the spin texture of the surface state Fermi surface [14] (also known as the Berry’s phase) bears a direct correspondence to the bulk topological invariant realized in the bulk electronic band structure via electronic band inversion [34, 37]. We experimentally show that a GP tunability can be realized on our magnetic films which is important to prepare the sample condition to the axion electrodynamics limit. On the Mn-Bi2 Se3 film, spin configuration pattern can be understood as a competition between the outof-plane TR breaking component and the in-plane helical component of spin. The in-plane spin that can be thought of winding around the Fermi surface in a helical pattern contributes to a nonzero GP [34], whereas the out-of-plane TR breaking spin direction is constant as one loops around the Fermi surface hence does not contribute to the Berry’s phase (GP). As a result, the GP remains almost π if the chemical potential lies at energies far away from the Dirac point, whereas it starts to decrease 182 and eventually reach to 0 as one approaches the TR breaking gap by lowering the chemical potential as discussed in theory [230], at least within the magnetic energy scale bz (Fig. 7.5). We show that this theoretical requirement can be experimentally achieved on the Mn-Bi2 Se3 surface via surface NO2 adsorption at various dosage levels. Fig. 7.5(a) shows the Mn(2.5%)-Bi2 Se3 surface states with in situ NO2 adsorption. The chemical potential is observed to be gradually shifted and finally placed within the magnetic gap. The associated phase (GP) at each experimentally achieved sample chemical potential [noted at the top-right corner of each panel in Fig. 7.5(a)] is found to gradually change from π to 0. The GP= 0 is the experimental condition for realizing axion electrodynamics with a topological insulator [223, 224]. With the chemical potential moved into the magnetic gap, the time-reversal breaking in-gap state features a singular hedgehog-like spin texture [Fig. 7.5(d)]. Such spin configuration simultaneous with the chemical potential placed within the magnetic gap [Fig. 7.5(d)] is the fundamental requirement for most of the theoretical proposals relevant to the utilization of magnetic topological insulators in novel devices [126,127,223,224,226]. Particularly, if Mn impurities form clusters on the surface of a 2D topological superconductor, the edges of these magnetic (time-reversal breaking) islands can exhibit helical Majorana edge states. We will further elaborate this exciting theoretical possibility in the next subsection. 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR Figure 7.1: Magnetic (Mn%) and non-magnetic (Zn%) doping on Bi2 Se3 films. (a),(b) Schematic layout and photograph of MBE grown Bi2 Se3 films used for the experiments. (c) Magnetization measurement at T = 45 K using magnetic circular dichroism shows out-of-plane ferromagnetic character of the Mn-Bi2 Se3 film (111) surface through the observed hysteretic response. Inset shows the measurement geometry. L(R)CP represents left(right)-handed circularly polarized light. (d) Electronic band dispersion of Mn(Zn)doped Bi2 Se3 MBE thin films along the M̄ − Γ̄ − M̄ momentum space cut. (e) Energymomentum distribution curves of Mn(Zn)-doped Bi2 Se3 samples. The energy scale associated with the spectral weight suppression (SWS) ESWS is observed as the energy spacing between the upper Dirac band minimum and the Dirac point location along the energy axis. This figure is adapted from Ref. [58]. 184 Figure 7.2: Temperature and doping dependence of magnetically induced changes on Mn-Bi2 Se3 surface. (a) The Mn atoms on the surface of the film are out-of-plane magnetically ordered, serving as a local magnetic field which results in the spin texture reorientation. (b) Two independent hysteresis measurements at T = 45 K using X-ray magnetic circular dichroism reveal the ferromagnetic character of the Mn-Bi2 Se3 film surface. The lower inset shows the remanent surface magnetization as a function of temperature. The out-of-plane magnetic hysteresis and ARPES gap were found to be correlated with each other. The upper inset shows the gap at the Dirac point in Mn(2.5%)-Bi2 Se3 film. (c) The spectral weight suppression energy scale ESWS and inverse momentum width 1/∆k of the surface states are shown as a function of Mn and Zn concentration measured at T = 20 K. (d) Temperature dependence of spectral weight suppression energy scale around the Dirac point of Mn(2.5%)-Bi2 Se3 film (as noted in Panel (c) by the dotted square). The ESWS decreases as temperature is raised signaling gradual weakening of magnetism. This figure is adapted from Ref. [58]. 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR Figure 7.3: Out-of-plane spin configuration measurements. Panels (a)-(d) present spin-resolved measurements on film I using 20 eV photons in the momentum distribution curve (MDC) mode. Panels (e)-(g) present spin-resolved measurements on film II using 9 eV photons in the energy distribution curve (EDC) mode. (a),(b) Spin-integrated data and corresponding MDCs. (c) Spin-resolved MDC spectra for out-of-plane direction as a function of electron binding energy. (d) Measured out-of-plane component of the spin polarization, presented in terms of respective out-of-plane polar angles (θ) defined in the inset of Panel (g). (e)-(f ) Spin-integrated dispersion and EDCs. The EDCs selected for detailed spin-resolved measurements are highlighted in green and red (Γ̄ momenta). (g) Measured out-of-plane spin polarization of the EDCs corresponding to Panel (f ). Inset ~ and the out-of-plane polar angle θ. The defines the definition of spin polarization vector P momentum value of each spin-resolved EDC is noted on the top. The polar angles (θ) of the spin vectors obtained from measurements are also noted. The 90◦ polar angle observed at Γ̄ suggests that the spin vector at Γ̄ momenta points in the vertical direction. The spin behavior at Γ̄ and its surrounding momentum space reveals a hedgehog-like spin configuration for each Dirac band separated by the gap, which breaks time-reversal symmetry (E(~k = 0, ↑)6=E(~k = 0, ↓)), as schematically shown in the inset of Panel (f ). This figure is adapted from Ref. [58]. 186 Figure 7.4: Spin configurations on non-magnetic samples. (a)-(d) Spin-resolved measurements on 1.5% non-magnetic Zn-Bi2 Se3 film. The in-plane polarization measurements (c) reveal the helical spin configuration, as in pure Bi2 Se3 topological insulator [34], suggesting that non-magnetic impurities do not induce spin reorientation on the topological surfaces. Out-of-plane measurements (d) show that no significant out-of-plane spin polarization Pz is induced near the Γ̄ point (a Kramers point), leaving the system timereversal invariant overall. (e)-(g) Spin-resolved ARPES measurements on ultra-thin undoped Bi2 Se3 film of three quintuple-layer thickness. The net spin polarization is found to be significantly reduced near the gap edge around the Γ̄ momenta. This is consistent with the fact that in ultra-thin films electrons tunnel between the top and bottom surfaces. (h),(i) A schematic of the two types of spin textures observed in our data. This figure is adapted from Ref. [58]. 7.1 HEDGEHOG SPIN TEXTURE IN A MAGNETIC TOPOLOGICAL INSULATOR Figure 7.5: Chemical potential tuned to lie inside the magnetic gap. (a) Measured surface state dispersion upon in situ NO2 surface adsorption on the Mn-Bi2 Se3 surface. The NO2 dosage in the unit of Langmuir (1 L = 1 × 10−6 torr·sec) and the tunable geometrical phase (see text) associated with the topological surface state are noted on the top-left and top-right corners of the panels, respectively. The red arrows depict the time-reversal breaking out-of-plane spin texture at the gap edge based on the experimental data. (b) Geometrical phase (GP) associated with the spin texture on the iso-energetic contours on the Mn-Bi2 Se3 surface as a function of effective gating voltage induced by NO2 surface adsorption. Red squares represent the GP experimentally realized by NO2 surface adsorption, as shown in Panel (a). GP= 0 (NO2 =2.0 L) is the condition for axion dynamics [224]. (c) The magnetic interaction strength bz (see text for definition), which corresponds to half of the magnetic gap magnitude, is obtained based on spin-resolved data sets (polar angle θ, momentum k) for Mn(2.5%)-Bi2 Se3 film II [see Figs. 7.3(e)-(g)]. (d) The time-reversal breaking spin texture features a singular hedgehog-like configuration when the chemical potential is tuned to lie within the magnetic gap, corresponding to the experimental condition presented in the last panel in Panel (a). (e),(f ) Spin texture schematic based on measurements of Zn-doped Bi2 Se3 film (60 QL), and 3 QL undoped ultra-thin film with chemical potential tuned onto the Dirac point energy or within the tunneling gap. This figure is adapted from Ref. [58]. 188 7.2 Helical Cooper pairing in topological insulator/superconductor heterostructures Realization of novel superconductivity is one of the central themes in condensed matter physics in general [2, 6, 53, 55, 125, 128, 225, 231–247]. Superconductivity is a collective phenomenon, where electrons moving to the opposite directions (±k) form dynamically bound pairs, resulting in a Cooper pair gas. In an ordinary superconductor, the conduction electrons that move along a certain direction have both spin-up and spin down electrons available for the Cooper pairing. The superconductivity observed so far, including in the conventional s-wave BCS superconductors as well as the cuprate or heavy fermion d-wave superconductors, all share this property. Recently, the discovery of 3D topological insulator in bismuth based semiconducting compounds have attracted much interest in condensed matter physics. In these TI materials, the bulk has a full energy gap while the surface exhibits an odd number of Dirac-cone electronic states, where the spin of the surface electrons is uniquely locked to their momentum [2, 6]. Therefore, at any given surface of a TI, the surface electrons moving to one direction (e.g. +k) will have only spin up electrons available whereas those of moving to −k only have spin down available. This is in contrast to the case in an ordinary superconductor, where at any given direction the conduction electrons will have both spin up and spin down available for the Cooper pairing. Such distinction can give rise to a wide range of exotic physics. Recently, a number of theories have highlighted these possibilities from both the fundamental physics and application point of view [125, 128, 225, 231–234]. For example, supersymmetry and Majorana fermions are both very interesting physics phenomena predicted in high energy theories that remain unobserved in particle physics experiments. And it has been theoretically predicted, very recently, that such new physics can be realized in a condensed matter setting [125, 128], if superconductivity can be induced in a spin- OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES helical gas. Moreover, a low energy realization of these phenomena can also be utilized to build the topological qubit for a topological quantum computer, which therefore is also of value in device applications. The first step towards the realization of any of the fascinating theoretical proposals requires a clear demonstration of the helical-Cooper pairing. Helical-Cooper pairing is defined as the superconducting Bose condensation of a spin-momentum locked Dirac electron gas, independent of the bosonic character of the pairing glue [2, 6]. To date, a direct experimental demonstration of the helical-Cooper pairing and their magnetic response remain elusive. Here we use spin- and momentum-resolved photoemission spectroscopy with sufficiently high resolution and at sufficiently low temperature to allow direct evidence for the helical Cooper pairing in a spin-momentum locked Dirac electron gas. We achieve this through the observation of momentum-resolved Bogoliubov quasi-particle spectrum of a topological insulator (Bi2 Se3 ) in proximity to a superconducting NbSe2 substrate. We further systematically investigate the dependence of the helical Cooper pairing in the Dirac electrons upon varying the TI film thickness or doping magnetic impurities. Our data show that the helical superconductivity in the Dirac surface states can be suppressed by introducing time-reversal symmetry breaking magnetic elements. Our observation of helical-Cooper pairing and superconductivity in spinDirac electronic gas serves as an important platform for realizing many exotic physics including emergent supersymmetry [128] physics. We also demonstrate a systematic methodology using the combination of spin- and momentum-resolved ARPES and interface transport that can be more generally applied to discover, isolate, and systematically optimize exotic superconductivity in engineered materials. Previous studies of superconductivity in topological insulator settings have been limited to transport and STM [53, 55, 235–243] High quality Bi2 Se3 / 2H-NbSe2 interface-heterostructures [Figs. 7.6(a),(b)] are prepared using molecular beam epitaxy growth (MBE). The growth conditions are 190 systematically optimized to enhance the superconductivity signals in our ARPES measurements. In order to protect the Bi2 Se3 surface from exposure to atmosphere, an amorphous selenium layer is deposited on top of the TI surface. This layer can be removed in situ in our angle-resolved photoemission spectroscopy (ARPES) experiments by annealing the samples. Fig. 7.6(c) shows the momentum-integrated ARPES intensity curves over a wide energy window (core-level spectra) taken on a representative 3 quintuple layer (QL) film before and after removing the amorphous selenium capping layer (decapping). High-resolution ARPES measurements on the Bi2 Se3 surface are then performed [Fig. 7.6(e)]. A sharp spectrum for the Dirac surface states is clearly observed, indicating a good surface/interface quality of our heterostructure. Consistent with previous studies of ultrathin TI films [58, 62, 80], we observe a gap at the Dirac point because of the hybridization between the top and bottom surfaces. Furthermore, we perform spin-resolved ARPES measurements (photon energy 50 eV) on the 4QL sample [Fig. 7.6(f)]. Our spin-resolved measurements confirm that the surface states are indeed singly degenerate near the Fermi level, which is at an energy level far away from the hybridization gap (v·kF > ∆hybr ) [58, 80]. At the Fermi level, a left-handed spin-momentum locking profile is observed, which is one of the critical ingredients for the helical-Cooper pairing as we will show in later sections. In order to study the possible proximity induced superconductivity in the Dirac surface states, we perform systematic ultra-low temperature (T ∼ 1 K) and ultra-high energy resolution (∼ 2 meV) ARPES measurements on these TI/superconductor heterostructures. We start with the 4QL sample using incident photon energy of 18 eV. Fig. 7.7(b) shows the measured dispersion of the Bi2 Se3 film. Both the topological surface states (TSSs) and the bulk conduction bands are observed. Six representative momenta, namely ±~k1 , ±~k2 , and ±~k3 are chosen for detailed studies, where k1 = 0.12 Å −1 −1 corresponds to the TSSs, and k2 = 0.08 Å −1 and k3 = 0.04 Å corre- spond to the outer and inner parts of the bulk band states, respectively. In order to OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES search for possible superconductivity signals, we study the ARPES energy-spectra at various momentum space locations in close vicinity to the Fermi level (EB = EF ± 5 meV). Fig. 7.7(c) shows the ARPES spectra at the momentum of k1 (TSSs) at different temperatures. Clear leading-edge shifts (superconducting gap) and coherence peaks are observed at low temperatures. The observed superconducting signals as temperature increases disappear at higher temperatures such as T = 7 K and 12 K. In order to better visualize the superconductivity gap in our data, the ARPES spectra are symmetrized with respect to the Fermi level, where the temperature evolution of the full (symmetrized) superconducting gap and the coherence peaks are clearly seen in Fig. 7.7(d). These measurements show the existence of induced superconductivity in the helical Dirac electrons occurring in the Bi2 Se3 TSSs, which is not possible in conventional momentum-integrated experiments that lacking spin resolution [53,55,235–243]. We compare and contrast the proximity induced superconductivity in the Dirac surface states to that of the bulk band states. Fig. 7.7(e) shows the ARPES spectra at k2 , where the bulk conduction bands are identified. Superconducting signals including leading edge shifts and coherence peaks are also observed at k2 . In order to obtain the magnitude of the superconducting energy gap, we fit the bulk state (±~k2 , and ±~k3 ) data by the Dynes function [248] [black curves in Fig. 7.7(g)], which is widely used in s-wave superconductors, whereas the surface state data (±~k1 ) is fitted by a BCS function with consideration of the spin-momentum locking and Dirac dispersion properties of the TSSs [blue curves in Fig. 7.7(g)]. Since the surface states and the bulk conduction bands co-exist at the chemical potential [Fig. 7.7(b)], we need to examine whether the observed superconducting proximity signal at k1 has contribution from the bulk bands. To further isolate the signals of Dirac surface states from the bulk bands, we choose another incident photon energy of 50 eV where we utilize the photoemission matrix element effect to suppress the spectral weight of the bulk conduction states. As shown in Fig. 7.7(i), at photon 192 energy of 50 eV, the bulk conduction band is almost completely suppressed and the only dispersive band near the Fermi level is the Dirac surface state. We subsequently study the spectra at the momentum k1 where the ARPES signal is dominated by the contribution from the surface states. Leading edge shifts and coherence peaks are clearly observed from k1 , which confirms the superconductivity in the Dirac surface states using a different photon energy. These systematic momentum-resolved measurements clearly show the existence of a superconducting helical electron gas, which is realized on the top surface of Bi2 Se3 grown on top of an s-wave superconductor NbSe2 . We perform ARPES measurements around the surface state Fermi surface as a function of Fermi surface azimuthal angle θ, to study the extent of anisotropy of the surface state superconducting gap. To isolate the surface state signal from the bulk, photon energy of 50 eV is used, where only surface states are observed near the Fermi level as seen in Fig. 7.8(a). Five representative momentum space cut-directions (θ1−θ5) are chosen as indicated by the dotted lines in Fig. 7.8(a). The helical-surface state superconducting gap observed by ARPES at different θ angles and their fits are shown in Fig. 7.8(b). The reasonably good surface state fitting results [blue curves in Figs. 7.7(g) and Fig. 7.8(b)] indicate that the obtained surface state superconductivity is consistent with its spin-helical and linear dispersive properties, which supports its helical-Cooper pairing nature. The obtained magnitude of superconducting order parameter is then plotted as a function of Fermi surface angle in Fig. 7.8(c). The superconducting gap is found to be nearly isotropic, which is also consistent with the time-reversal invariant helical nature of the surface state superconductivity as expected theoretically [125, 225]. We note that the helical Cooper pairing in the topological surface states as observed here is also different from that of in other singly degenerate (spin-momentum locked) but non-topological systems. For example, in a Rashba-2DEG, although the electrons are also singly degenerate, but along any OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES k−direction, there are still both spin up and spin down electrons available for Cooper pairing [see Fig. 7.8(e)]. Therefore, only in the topological surface state, there are electrons with only one spin available for the Cooper pairing along any k−direction [Fig. 7.8(d)]. This unique property as demonstrated here (which we refer as the helical Cooper pairing) is indispensable for all the fascinating phenomena as predicted in theories [125, 128, 225, 231–234]. In Fig. 7.8(f), we present model calculation analysis, which shows a px ±ipy superconducting order parameter in the Dirac surface states, supporting the helical Cooper pairing nature. Therefore, through our systematic ARPES measurements with simultaneous energy, momentum and spin resolution, we observe superconductivity in an odd number of spin-momentum locked Dirac surface states, which serves as the direct experimental evidence for the helical-Cooper pairing. We study the observed superconductivity in the surface states as a function of surface-to-surface hybridization strength (effectively as a function of the TI film thickness), in order to experimentally prove its proximity-induced nature. As shown in Fig. 7.9(a), a sample with a Dirac point hybridization gap as large as ∼ 200 meV is realized in a 3QL film sample. Clear leading-edge shifts, coherence peaks and their temperature evolution are observed in the TSSs near the Fermi energy [Figs. 7.9(b),(c)] evidence for the helical-Cooper pairing and helical superconductivity in the 3QL film samples. The observed surface state superconducting gap value is about 0.7 − 0.8 meV. We now turn to a gapless (7QL) sample as shown in Fig. 7.9(d). The absence of hybridization gap at the Dirac point reveals that surface state wavefunctions from the top and the interface surfaces are completely separated in real space. Finite superconductivity signals are observed in the ARPES spectra at both momenta of k1 (Dirac surface states) and k2 (bulk conduction states), which are found to be weaker than the gapped samples. The Bi2 Se3 top surface’s superconducting gap as a function of Dirac point gap value (surface-to-surface hybridization strength) is shown in Figs. 7.9(g),(h) in a (surface and bulk) band-resolved fashion. It can be seen that the 194 induced superconducting gap near the top surface increases with a larger the Dirac point hybridization gap, which is realized in thinner TI films. This observation is qualitatively consistent with the theoretical description of the superconducting proximity effect, where the Cooper pair potential on the top surface is enhanced with the decreasing thickness of the normal metal. More interestingly, it can be seen that the surface state superconducting gap increases at a faster rate than that of the proximity gap on the bulk band. Such contrast reveals that stronger surface-to-surface hybridization significantly enhances the helical pairing in the surface states on the top surface. These microscopics of the superconducting proximity effect observed in our data will be a valuable guide in properly interpreting the vast complexity of the transport data addressing the proximity effects in TI films and heterostructures. In order to test the time-reversal invariant character of surface state superconductivity of Bi2 Se3 required by its helical nature, we study manganese (Mn) doped Bi2 Se3 grown on top of NbSe2 . Mn atoms are introduced into Bi2 Se3 throughout the film during the MBE growth. ARPES studies on 4QL Bi2 Se3 films with two different Mn doping (4% and 10%) levels are presented in Figs. 7.10(a)-(f). Bulk manganese doping is found to hole dope the system, thus bringing the chemical potential closer to the Dirac point. In principle, Mn impurities can affect the induced superconductivity in several different channels, all leading to the suppression of proximity superconductivity: The major effect is that Mn impurities introduce (either random or ordered) magnetism into the TI, which is destructive to the helical pairing; Another minor effect, which can also contribute, is that impurities generate random disorder reducing the electron mean free path. As shown in Figs. 7.10(a)-(f), the superconducting coherence peak is strongly suppressed in the heavily Mn-doped samples. These momentum-resolved measurements allow us to isolate the strength of the effect on helical surface states and bulk bands, thus directly demonstrating that magnetic impurities lead to strong pairing breaking in both conventional and helical OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES pairing channels. The complete suppression of superconductivity in the helical Dirac surface states upon strong Mn doping effectively drives a topological phase transition from a helical superconductor to a normal Dirac metal state as seen in our data. A sample fabricated to lie near the critical point of this transition can host many exotic phenomena (which will be discussed later in this paper). In order to check that the top surface superconductivity is indeed a proximity effect, we use the well-established methodology of point-contact Andreev reflection measurements to compare the induced gap values at the NbSe2 /Bi2 Se3 heterointerface. The point contract probe is characterized by measurements on pure NbSe2 [249]. The point-contact spectra on a NbSe2 /Bi2 Se3 (16QL) heterostructure sample are shown in Fig. 7.12(a). At temperatures below the Tc (∼ 7.2 K) of NbSe2 , the differential conductance (dI/dV ) around zero bias increases as a result of the Andreev reflection process, similar to the bare NbSe2 spectra. Interestingly, a second differential conductance increase appears below ∼ 5 K. The sharp rise of differential conductance corresponds to the energy gap of the superconducting layer. From the data, we obtain the larger gap (∆1 ) changing from 0 to 1.3 ± 0.2 mV from 7.5 K to 3.0 K. The second gap (∆2 ) feature changes from 0 to 0.8 ± 0.2 mV from 5.0 K to 3.0 K. Similar two gap features have been observed in point-contact studies of Ag/Pb [250] and Si/Nb [251] interface samples and were attributed to the superconducting energy gap of the superconducting layer and the proximity induced gap in the normal metal layer at the N/S interface, respectively. Injected electrons from the point-contact are Andreev reflected inside the superconducting Bi2 Se3 proximity layer if their energies are lower than the induced superconducting gap in Bi2 Se3 . When their energies are above the induced gap ∆TI but below the NbSe2 superconducting gap ∆SC , injected electrons are not affected by the order parameter in the Bi2 Se3 layer but Andreev reflected in the NbSe2 region. Therefore, the edge around ∆1 is likely due to the NbSe2 gap, while the sharp edge around ∆2 in the conductance spectrum is likely to reflect the induced 196 gap in Bi2 Se3 near the interface. It is worth noting that unlike ARPES, which is mostly sensitive to the top surface, the point-contact transport probes deeper into the superconductor, similar to the electron mean free path, which is estimated to be ∼16 nm in our films. The induced gap in Bi2 Se3 at the Bi2 Se3 /NbSe2 interface is ∼0.8 meV at 3 K from the point-contact measurement, which is in reasonable agreement with the fitted gap value extracted from the ARPES measurement (see data on 3QL sample). Our results thus suggest that the combination of ARPES and point-contact transport together provides a powerful method for probing superconducting proximity effect which can be used to correlate the proximity gap on the top surface and the buried interface if film thickness is not too large (not larger than the superconducting coherence length). In contrast to idealized theoretical models [125, 225] of topological superconductivity where only Dirac surface states cross the Fermi level, real samples exhibit a complex phenomenology due to the coexistence of multiple bands at the chemical potential, as demonstrated in our data above. Thus, the interpretation of experimental studies must take into account both the desirable Cooper pairing from the Dirac surface states and conventional superconductivity from the bulk, trivial surface states and impurity surface states. The coexistence of multiple bands at the Fermi level means that any superconductivity realized in actual TI materials consist of not only the desirable helical Cooper pairing from the Dirac surface states but also conventional superconductivity from the bulk states, as shown above in our data. We note that although progress has been reported by using conventional transport and STM experiments [53,55,235–243], those studies do not have the spin and momentum resolution necessary to distinguish the helical Cooper pairing from that of the conventional superconductivity from other bands that intermix at the interface making interpretation of Majorana fermions unreliable or complex. Hence a direct experimental demonstration of the existence of superconductivity in the helical Cooper OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES pairing channel remained elusive before our momentum and spin space observations reported here. In fact, it has been recently shown both theoretically and experimentally [244–247] that the conventional superconductivity in the bulk and impurity bands at the interface or surface lead to ambiguous interpretations of the transport and STM data. In order to achieve a clear case for Majorana zero mode, the helical component of the Cooper pairing must be isolated, as demonstrated here. Therefore, it is in this context that our observation of helical Cooper pairing and superconductivity in a half Dirac gas is of critical importance. Additionally, the overall methodology employed here can be applied to isolate helical Cooper pairing in other systems and in connection to a feedback loop for material growth for the optimization of the helical channel. We also note that our systematic studies (by observing the superconducting gap (leading edge shift), the clear coherence peak, as well as their systematic dependence upon varying temperature, TI film thickness and doping magnetic impurities) are in contrast to the debatable ARPES results on Bi2 Se3 /BSCCO samples [83, 84, 252]. In that case, no superconducting coherence peak was observed [83,84,252], and the claim of a ≥ 15 meV leading edge shift [252] in the Dirac surface states in Bi2 Se3 /BSCCO is in contrast to the absence of any observable leading edge shift in the other two studies [83, 84]. In fact, a strong superconducting proximity effect is inconsistent with important facts including the severe mismatch of both Fermi momenta and crystal symmetries between Bi2 Se3 and BSCCO, very short out-of-plane superconducting coherence length of high-Tc superconductors, as well as the different superconducting pairing symmetries between a TI and a d−wave cuprate superconductor. Thus, our data strongly supports the view that TI/NbSe2 is a more ideal platform than TI/BSCCO for the proposed novel physics if the system can be further optimized increasing helical Cooper pairing channel by tuning the material parameters. We discuss the emergent topological phenomena that can be enabled by our iden198 tification of helical-Cooper pairing. One exciting scenario is to realize supersymmetric phenomenon in our experimental setup [128] by further improvement of the film quality and magnetic doping process. As shown in Fig. 7.12(d), magnetic doping or an external in-plane magnetic field is necessary to drive the system to the critical point between the helical superconductivity and the normal Dirac gas states, with the chemical potential tuned to the Dirac point [demonstrated in Fig. 7.12(b)]. Under this condition, theory predicts that topological surface states (a fermionic excitation) and the fluctuations of superconducting order (a bosonic excitation) satisfy supersymmetry relationship, and therefore, strikingly, possess the same Fermi/Dirac velocity and same lifetime or self-energy [128]. While the superpartners of elementary particles in high energy physics have never been experimentally observed, the experimental methodologies, artificial sample fabrication control and experimental observations reported here pave the way for simulating and testing supersymmetric physics concepts in future sub-Kelvin nanodevices fabricated out of sample configurations discussed here. Another very exciting proposal is to deposit magnetic impurities on the surface of our TI/SC heterostructure samples [2]. Since the superconducting topological Dirac surface states naturally realize a 2D helical topological superconductor [61,125], a ferromagnetic island (or a cluster) can create a local non-superconducting region (Fig. 7.11). In this case, the edge of the magnetic island corresponds to the boundary between a topological superconductor and a normal (non-topological) state and is therefore expected to feature helical Majorana edge modes, which can be readily detected by advanced spatial-resolved spectroscopic probes such as scanning tunneling spectroscopy. OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES Figure 7.6: Topological superconductivity via proximity effect. (a) A schematic layout of ultra-thin Bi2 Se3 films epitaxially grown on the (0001) surface of single crystalline s-wave superconductor 2H-NbSe2 (Tc = 7.2 K) using the MBE technique. (b) High resolution transmission electron microscopy (TEM) measurements of the Bi2 Se3 /NbSe2 interface at 200 keV electron energy. An atomically abrupt transition from NbSe2 layered structure to the layered quintuple layer structure of Bi2 Se3 is resolved, showing a good atomically flat interface crystal quality. (c) Momentum-integrated ARPES intensity curves over a wide binding energy window (core-level spectra) taken on a representative 3QL Bi2 Se3 (≃ 3 nm) film grown on NbSe2 before and after removing the amorphous selenium capping layer (decapping). (d) A low-energy electron diffraction (LEED) image on a 4QL Bi2 Se3 film shows six-fold pattern providing evidence that the thin Bi2 Se3 film is well-ordered. (e) High-resolution ARPES dispersion map of a 4QL Bi2 Se3 film on NbSe2 after decapping using incident photon energy of 50 eV. The white circle and cross schematically show the measured direction of the spin texture on the top surface of our 4QL Bi2 Se3 film shown in Panel (f ). (f ) Spin-resolved ARPES measurements on 4QL Bi2 Se3 as a function of binding energy at a fix momentum which is indicated by the white dotted line in Panel (e). (g) High-resolution ARPES dispersion map of a 6QL Bi2 Se3 film on NbSe2 at T = 12 K. The white arrow indicates the momentum for the temperature dependent EDC in Panel (h). (h) Temperature dependence of the ARPES spectra in Panel (g). This figure is adapted from Ref. [61]. 200 Figure 7.7: Momentum resolved helical 2D topological superconductivity. (a) ARPES dispersion maps of Bi2 Se3 /NbSe2 as a function of Bi2 Se3 film thickness. All dispersion maps are measured with photon energy of 50 eV, except the 7QL sample which is measured by 18 eV. The blue arrows quantitatively depict the spin texture configuration in the ultra-thin limit. The length of the arrow is proportional to the magnitude of the spin polarization. (b) ARPES dispersion map of a 4QL Bi2 Se3 film measured at T = 12 K using incident photon energy of 18 eV. (c) ARPES spectra at the fixed momentum of k1 (the topological surface states). (d) Symmetrized ARPES spectra at k1 . (e) ARPES spectra at the fixed momentum of k2 (bulk band states). (f ),(g) Symmetrized ARPES spectra at ±k1 , ±k2 , and ±k3 at T ∼ 1 K. The surface state gap (±k1 ) is fitted by a BCS function considering its spin-momentum locking and Dirac dispersion properties, where as the bulk gap is fitted by the Dynes function [248]. (h) ARPES spectrum of the in situ evaporated gold film, where the kinetic energy of the Fermi level and the energy resolution are determined. (i) ARPES dispersion map of a 4QL Bi2 Se3 film measured with incident photon energy of 50 eV. (j),(k) ARPES spectra at the fixed momentum of k1 . The insets of Panels (c),(j) show an ARPES dispersion map near the Fermi level at low temperature of T ∼ 1 K at photon energies of 18 eV and 50 eV, respectively. This figure is adapted from Ref. [61]. OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES Figure 7.8: Topological superconducting gap and helical pairing magnitude. (a) Fermi surface map taken at incident photon energy of 50 eV. The white dotted lines indicate the momentum-space cut-directions chosen to study the surface state superconducting gap as a function of Fermi surface angle θ around the surface state Fermi surface. (b) Symmetrized and normalized ARPES spectra along θ1 through θ5 respectively (red) and their surface gap fittings. (c) Fermi surface angle dependence of the estimated superconducting gap around the surface state Fermi surface. (d) Illustrations for helical-Cooper pairing in a spin-momentum locked helical electron gas and (e) The conventional s-wave Cooper pairing in an ordinary superconductor. Note that the superconductivity in a Rashba-2DEG can be visualized also in the same schematic [Panel (e)] but with the length of the k-vector for spin up and spin down electrons being different (spin-split). However, for a Rashba-2DEG, it is still true that along any k-direction, both spin up and spin down electrons cross the Fermi level and are available for the Cooper pairing. (f ) Model calculation results of a topological insulator film in proximity to an s-wave superconductor shows the calculated e S ) and triplet (∆ eT) total superconducting pairing amplitude and its decomposed singlet (∆ components on the top surface of a 4-unit-cell thick TI interfaced with an s-wave superconductor, which further confirms the helical (topologically nontrivial) nature of the induced e is a dimensionless, we denote surface state superconductivity in our Bi2 Se3 films. Since ∆ e to differentiate from the superconducting gap ∆ measured in experiments. This a tilde ∆ figure is adapted from Ref. [61]. 202 Figure 7.9: Hybridization dependence of bulk superconducting gap vs. topological superconducting gap. (a) ARPES dispersion map of a 3QL Bi2 Se3 film measured at T = 12 K using incident photon energy of 50 eV. (b) ARPES spectra at the fixed momentum of k1 at different temperatures. (c) Symmetrized ARPES spectra at different temperatures. (d) ARPES dispersion map of a 7QL Bi2 Se3 film measured at T = 12 K using incident photon energy of 18 eV. (e),(f ) ARPES spectra at the fixed momenta of k1 and k2 . (g) ARPES measured superconducting gap for topological surface states (k1 ) and for the bulk conduction states (k2 ) as a function of Dirac point gap value (surface-to-surface hybridization strength). The dotted lines are guides to the eye. (h) Surface-to-surface hye TI in calculation is a bridization dependence in calculation. Since the pairing amplitude ∆ dimensionless number, we normalize it by the pairing amplitude of the substrate supercone Substrate (a constant). This figure is adapted from Ref. [61]. ductor ∆ OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES Figure 7.10: Destruction of the helical Cooper pairing via time-reversal symmetry breaking magnetic doping. (a) ARPES dispersion map of a 4QL Mn(4%)-doped Bi2 Se3 film measured at T ∼ 1 K. (b),(c) ARPES spectra at the fixed momenta of k1 (topological surface states) and k2 (bulk conduction states). (d)-(f ) Same as Panels (a)-(c) but for 10% Mn doping. The Mn concentrations indicated here are nominal, which means they are estimated by the flux ratio of Mn flux : Bi flux during the MBE growth. This figure is adapted from Ref. [61]. 204 Figure 7.11: A proposal to realize Majorana edge-modes by creating ferromagnetic islands on the surface of a 2D helical topological superconductor. OOPER PAIRING IN TOPOLOGICAL INSULATOR/SUPERCONDUCTOR HETEROSTRUCTURES Figure 7.12: Point-contact interface transport and conditions for theoretically predicted emergent supersymmetry. (a) Point-contact transport (dI/dV vs bias voltage) as a function of temperature. For T = 3.5 K, below the Tc of NbSe2 , as the bias voltage is swept from ±3mV to 0mV, dI/dV first increases, then levels off at |V | ≃ 1.3 mV, and then increases again, reaching a maximum at |V | ≃ 0.8 mV. dI/dV for other T < Tc exhibits a similar behavior. This indicates two Andreev reflection channels with different sizes of superconducting gap. The inset illustrates the two Andreev reflection processes via the induced superconducting gap in Bi2 Se3 and intrinsic superconducting gap in NbSe2 , respectively. (b) Measured surface state dispersion upon in situ NO2 surface adsorption on the surface of a 7QL Bi2 Se3 /NbSe2 sample using incident photon energy of 55 eV at temperature of 20 K. The NO2 dosage in the unit of Langmuir (1L = 1 × 10−6 torr·sec) is noted on the top-right corners of the panels, respectively. The white dotted lines in the last panel are guides to the eye. (c),(d) Theoretically proposed [128] unusual criticality related to supersymmetry phenomena can be realized in the topological insulator/s-wave superconductor interface as the chemical potential is tuned to the surface state Dirac point and an in-plane magnetization drives the system to the critical point between superconducting and normal Dirac metal phases. Fermions and bosons are expected to feature the same band velocity and quasi-paticle lifetime [128], where fermion velocity is estimated to be around 5 × 105 m/s from our ARPES result. This cartoon refers to a future possibility. This figure is adapted from Ref. [61]. 206 Bibliography [1] N. W. Ashcroft & N. D. Mermin, Solid State Physics (Holt, Rinehart and Winston, New York, 1976). [2] M. Z. Hasan & C. L. Kane, Colloquium: Topological Insulators. Rev. Mod. Phys. 82, 3045-3067 (2010). [3] J. E. Moore, The birth of topological insulators. Nature 464, 194-198 (2010); C.L. Kane and J. E. Moore, Topological insulators. Physics World 24, 32-36 (2011). [4] X. -L. Qi & S. -C. Zhang, The quantum spin Hall effect and topological insulators. Phys. Today 63, 33-38 (2010). [5] M. Z. Hasan & J. E. Moore, Three-Dimensional Topological Insulators. Ann. Rev. Cond. Mat. Phys. 2, 55-78 (2011). [6] X. -L. Qi & S. -C. Zhang, Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057-1110 (2011). [7] M. Z. Hasan, Su-Yang Xu, D. Hsieh, L. A. Wray & Y. Xia, Topological Surface States: A New Type of 2D Electron Systems. in Topological Insulators edited by M. Franz and L. Molenkamp (Elsevier, Oxford 2013). 207 BIBLIOGRAPHY [8] C.-X Liu & S.-C. Zhang, Models and Materials for Topological Insulators. in Topological Insulators edited by M. Franz and L. Molenkamp (Elsevier, Oxford 2013). [9] K. He, Y. Wang & Qi-Kun Xue, Quantum anomalous Hall effect. Natl. Sci. Rev. 1, 39-49 (2014). [10] A. M. Turner & A. Vishwanath, Beyond Band Insulators: Topology of Semimetals and Interacting Phases. Preprint at http://arXiv:1301.0330 (2013). [11] T. Okuda & A. Kimura, Spin- and Angle-Resolved Photoemission of Strongly SpinOrbit Coupled Systems. J. Phys. Soc. Jpn. 82, 021002 (2013). [12] Y. Ando, Topological Insulator Materials. J. Phys. Soc. Jpn. 82, 102001 (2013). [13] M. Z. Hasan Liu, Su-Yang Xu & M. Neupane, Topological Insulators, Topological Crystalline Insulators, and Topological Kondo Insulators. Preprint at http://arXiv:1406.1040 (2014). [14] L. Fu, C. L. Kane & E. J. Mele, Topological Insulators in Three Dimensions. Phys. Rev. Lett. 98, 106803 (2007). [15] R. Roy, Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009). [16] J. E. Moore & L. Balents, Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306(R) (2007). [17] D. Hsieh et al., A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970-974 (2008). [Completed and submitted in 2007]. Also see KITP Proceeding at http://online.itp.ucsb.edu/online/motterials07/hasan/ (2007). 208 BIBLIOGRAPHY [18] D. Hsieh et al., Observation of Unconventional Quantum Spin Textures in Topological Insulators. Science 323, 919-922 (2009). [This paper that reveals spintexture and spin-momentum locking thus the symmetry-protected Z2 topological state was submitted in 2008.] [19] K. v. Klitzing, G. Dorda & M. Pepper, New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 45, 494-497 (1980). [20] R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations. Phys. Rev. Lett. 50, 1395-1398 (1983). [21] D. J. Thouless et al., Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 49, 405-408 (1982). [22] J. E. Avron, D. Osadchy & R. Seiler, A Topological Look at the Quantum Hall Effect. Phys. Today 56(8), 38-42 (2003). [23] D. C. Tsui, H. L. Stormer & A. C. Gossard, Two-Dimensional Magnetotransport in the Extreme Quantum Limit. Phys. Rev. Lett. 48, 1559-1562 (1982). [24] X.-G. Wen, Topological Orders in Rigid States. Int. J. Mod. Phys. B 4, 239-271 (1990). [25] F. D. M. Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 61, 2015-2018 (1988). [26] C. L. Kane & E. J. Mele, Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95, 146802 (2005). BIBLIOGRAPHY [27] B. A. Bernevig, T. L. Hughes & S.-C. Zhang, Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 314, 1757-1761 (2006). [28] M. König et al., Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 318, 766-770 (2007). [29] L. Fu & C. L. Kane, Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007). [30] D. Hsieh et al., A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970-974 (2008). [31] D. Hsieh et al., Observation of Unconventional Quantum Spin Textures in Topological Insulators. Science 323, 919-922 (2009). [32] Y. Xia et al., Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398-402 (2009). [33] H. Zhang et al., Topological insulators in Bi2 Se3 , Bi2 Te3 and Sb2 Te3 with a single Dirac cone on the surface. Nature Phys. 5, 438-442 (2009). [34] D. Hsieh et al., A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101-1105 (2009). [35] Y. L. Chen et al., Experimental Realization of a Three-Dimensional Topological Insulator, Bi2 Te3 . Science 325, 178-181 (2009). [36] D. Hsieh et al., Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2 Te3 and Sb2 Te3 . Phys. Rev. Lett. 103, 146401 (2009). [37] Su-Yang Xu et al., Topological phase transition and texture inversion in a tunable topological insulator. Science 332 560-564 (2011). 210 BIBLIOGRAPHY [38] T. Sato et al., Unexpected mass acquisition of Dirac fermions at the quantum phase transition of a topological insulator. Nature Phys. 7, 840-844 (2011). [39] P. Dziawa et al., Topological crystalline insulator states in Pb1−x Snx Se. Nature Mat. 11, 1023-1027 (2012). [40] Su-Yang Xu et al., Observation of a topological crystalline insulator phase and topological phase transition in Pb1−x Snx Te. Nature Commun. 3, 1192 (2012). [41] Y. Tanaka et al., Experimental realization of a topological crystalline insulator in SnTe. Nature Phys. 8, 800-803 (2012). [42] Y. Okada et al., Observation of Dirac node formation and mass acquisition in a topological crystalline insulator. Science 341, 1496-1499 (2013). [43] M. Neupane et al., Observation of a topological 3D Dirac semimetal phase in high-mobility Cd3 As2 . Nature Commun. 5, 4786 (2014). [44] S. Borisenko et al., Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014). [45] Z. K. Liu et al., Discovery of a three-dimensional topological Dirac semimetal, Na3 Bi. Science 343, 864-867 (2014). [46] Su-Yang Xu et al., Fermi Arc Surface States in a Topological Metal: A New Type of 2D Electron Gas. DOI:10.1126/science.1256742 Science (2014). [47] Su-Yang Xu et al., Observation of a bulk 3D Dirac multiplet, Lifshitz transition, and nestled spin states in Na3 Bi. Preprint at http://arXiv:1312.7624 (2013). [48] Z. K. Liu et al., A stable three-dimensional topological Dirac semimetal Cd3 As2 . Nature Mater. 13, 677-681 (2014). BIBLIOGRAPHY [49] N. Xu et al., Surface and Bulk Electronic Structure of the Strongly Correlated System SmB6 and Implications for a Topological Kondo Insulator. Phys. Rev. B 88, 121102(R) (2013). [50] M. Neupane et al., Surface electronic structure of the topological Kondo-insulator candidate correlated electron system SmB6 . Nature Commun. 4, 2991 (2013). [51] J. Jiang et al., Observation of in-gap surface states in the Kondo insulator SmB6 by photoemission. Nature Commun. 4, 3010 (2013). [52] E. Frantzeskakis et al., Kondo hybridisation and the origin of metallic states at the (001) surface of SmB6 . Phys. Rev. X 3, 041024 (2014). [53] Y. S. Hor et al., Superconductivity in Cux Bi2 Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010). [54] L. A. Wray et al., Observation of topological order in a superconducting doped topological insulator. Nature Phys. 6, 855-859 (2010). [55] B. Sacépé et al., Gate-tuned normal and superconducting transport at the surface of a topological insulator. Nature Commun. 2, 575 (2011). [56] Y. S. Hor et al., Development of ferromagnetism in the doped topological insulator Bi2−x Mnx Te3 . Phys. Rev. B 81, 195203 (2010). [57] L. A. Wray et al., A topological insulator surface under strong Coulomb, magnetic and disorder perturbations. Nature Phys. 7, 32-37 (2011). [58] Su-Yang Xu et al., Hedgehog spin texture and Berry’s phase tuning in a magnetic topological insulator. Nature Phys. 8, 616-622 (2012). [59] J. G. Checkelsky et al., Dirac-fermion-mediated ferromagnetism in a topological insulator. Nature Phys. 8, 729-733 (2012). 212 BIBLIOGRAPHY [60] C.-Z. Chang et al., Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 340, 167-170 (2013). [61] Su-Yang Xu et al., Momentum space imaging of Cooper pairing in a half Dirac gas topological superconductor. Nature Phys. doi:10.1038/nphys3139 (2014). [62] Y. Zhang et al., Crossover of the three-dimensional topological insulator Bi2 Se3 to the two-dimensional limit. Nature Phys. 6, 584-588 (2010). [63] Su-Yang Xu et al., Discovery of several large families of Topological Insulator classes with backscattering-suppressed spin-polarized single-Dirac-cone on the surface. Preprint at http://arXiv:1007.5111 (2010). [64] K. Kuroda et al., Experimental Realization of a Three-Dimensional Topological Insulator Phase in Ternary Chalcogenide TlBiSe2 . Phys. Rev. Lett. 105, 146801 (2010). [65] Su-Yang Xu et al., Realization of an isolated Dirac node and strongly modulated Spin Texture in the topological insulator Bi2 Te3 . Preprint at http://arXiv:1101.3985 (2011). [66] S. Souma et al., Direct Measurement of the Out-of-Plane Spin Texture in the Dirac-Cone Surface State of a Topological Insulator. Phys. Rev. Lett. 106, 216803 (2011). [67] C. Jozwiak et al., Widespread spin polarization effects in photoemission from topological insulators. Phys. Rev. B 84, 165113 (2011). [68] P. D. C. King et al., Large tunable Rashba spin splitting of a two-dimensional electron gas in Bi2 Se3 . Phys. Rev. Lett. 107 096802 (2011). BIBLIOGRAPHY [69] Su-Yang Xu et al., Anomalous spin-momentum locked two-dimensional states in the vicinity of a topological phase transition. Preprint at http://arXiv:1204.6518 (2012). [70] S. V. Eremeev et al., Atom-specific spin mapping and buried topological states in a homologous series of topological insulators. Nature Commun. 3, 635 (2012). [71] Su-Yang Xu et al., Dirac point spectral weight suppression, surface ‘gaps’, and ‘twin-peak’ intensity profiles in nonmagnetic and magnetic topological insulators. Preprint at http://arXiv:1206.0278 (2012). [72] S. Kim et al., Surface Scattering via Bulk Continuum States in the 3D Topological Insulator Bi2 Se3 . Phys. Rev. Lett. 107, 056803 (2012). [73] Z. Pan et al., Photoemission Spectroscopy of Magnetic and Nonmagnetic Impurities on the Surface of the Bi2 Se3 Topological Insulator. Phys. Rev. Lett. 108, 117601 (2012). [74] M. Neupane et al., Topological surface states and Dirac point tuning in ternary topological insulators. Phys. Rev. B 85, 235406 (2012). [75] M. Brahlek et al., Topological-metal to band-insulator transition in (Bi1−x Inx )2 Se3 thin films. Phys. Rev. Lett. 109, 186403 (2012). [76] Y. H. Wang & N. Gedik, Circular dichroism in angle-resolved photoemission spectroscopy of topological insulators. Phys. Status Solidi RRL 7, 64-71 (2013). [77] Z.-H. Zhu et al., Layer-By-Layer Entangled Spin-Orbital Texture of the Topological Surface State in Bi2 Se3 . Phys. Rev. Lett. 110, 216401 (2013). [78] M. Neupane et al., Oscillatory surface dichroism of the insulating topological insulator Bi2 Te2 Se.Phys. Rev. B 88, 165129 (2013). 214 BIBLIOGRAPHY [79] Chang Liu et al., Spin correlated electronic state on the surface of a spin-orbit Mott system (Layered Iridates). Phys. Rev. B 90, 045127 (2014). [80] M. Neupane et al., Observation of Quantum-Tunneling Modulated Spin Texture in Ultrathin Topological Insulator Bi2 Se3 Films. Nature Commun. 5, 3841 (2014). [81] M. Neupane et al., Saddle point singularity and topological phase diagram in a tunable topological crystalline insulator (TCI). Preprint at http://arXiv:1403.1560 (2014). [82] J. Sánchez-Barriga et al., J. Photoemission of Bi2 Se3 with Circularly Polarized Light: Probe of Spin Polarization or Means for Spin Manipulation? Phys. Rev. X 4, 011046 (2014). [83] Su-Yang Xu et al., Search for superconducting proximity effect in a topological insulator and high temperature superconductor heterostructure Bi2 Se3 /Bi2 Sr2 CaCu2 O8+δ . Phys. Rev. B, 90 085128 (2014). [84] T. Yilmaz et al., Absence of a Proximity Effect in a Topological Insulator on a Cuprate Superconductor: Bi2 Se3 /Bi2 Sr2 CaCu2 O8 . Phys. Rev. Lett. 113, 067003 (2014). [85] M. Xia et al., Angle-resolved Photoemission Spectroscopy Study on the Surface States of the Correlated Topological Insulator YbB6 . Sci. Rep. 5999 (2014). [86] M. Neupane et al., Observation of non-Kondo-like electronic structure in strongly correlated electron system YbB6 . Preprint at http://arXiv:1404.6814 (2014). [87] N. Xu et al., Surface vs bulk electronic structures of a moderately correlated topological insulator YbB6 revealed by ARPES. Preprint at http://arXiv:1405.0165 (2014). BIBLIOGRAPHY [88] P. Roushan et al., Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106-1109 (2009). [89] T. Zhang et al., Experimental Demonstration of Topological Surface States Protected by Time-Reversal Symmetry. Phys. Rev. Lett. 103, 266803 (2009). [90] Z. Alpichshev et al., STM Imaging of Electronic Waves on the Surface of Bi2 Te3 : Topologically Protected Surface States and Hexagonal Warping Effects. Phys. Rev. Lett. 104, 016401 (2010). [91] P. Cheng et al., Landau Quantization of Topological Surface States in Bi2 Se3 . Phys. Rev. Lett. 105, 076801 (2010). [92] T. Hanaguri et al., Momentum-resolved Landau-level spectroscopy of Dirac surface state in Bi2 Se3 . Phys. Rev. B 82, 081305 (2010). [93] H. Beidenkopf et al., Spatial fluctuations of helical Dirac fermions on the surface of topological insulators. Nature Phys. 7, 939-943 (2011). [94] Y. Okada et al., Direct Observation of Broken Time-Reversal Symmetry on the Surface of a Magnetically Doped Topological Insulator. Phys. Rev. Lett. 106, 206805 (2011). [95] I. Zeljkovic et al., Mapping the unconventional orbital texture in topological crystalline insulators. Nature Phys. 10, 572-577 (2014). [96] D.-X. Qu et al., Quantum Oscillations and Hall Anomaly of Surface States in the Topological Insulator Bi2 Te3 . Science 329, 821-824 (2010). [97] J. G. Analytis et al., Two-dimensional surface state in the quantum limit of a topological insulator. Nature Phys. 6, 960-964 (2010). [98] H. L. Peng et al., Aharonov-Bohm interference in topological insulator nanoribbons. Nature Mater. 9, 225-229 (2010). 216 BIBLIOGRAPHY [99] H. Steinberg et al., Surface State Transport and Ambipolar Electric Field Effect in Bi2 Se3 Nanodevices. Nano Lett. 10, 5032-5036 (2010). [100] J. Chen et al., Gate-Voltage Control of Chemical Potential and Weak Antilocalization in Bi2 Se3 . Phys. Rev. Lett. 105, 176602 (2010). [101] H. T. He et al., Impurity Effect on Weak Antilocalization in the Topological Insulator Bi2 Te3 . Phys. Rev. Lett. 106, 166805 (2011). [102] M. Liu et al., Electron interaction-driven insulating ground state in Bi2 Se3 topological insulators in the two-dimensional limit. Phys. Rev. B 83, 165440 (2011). [103] J. Wang et al., Evidence for electron-electron interaction in topological insulator thin films. Phys. Rev. B 83, 245538 (2011). [104] D. Kim et al., Surface conduction of topological Dirac electrons in bulk insulating Bi2 Se3 . Nature Phys. 8, 459-463 (2012). [105] Z. Ren et al., Fermi level tuning and a large activation gap achieved in the topological insulator Bi2 Te2 Se by Sn doping. Phys. Rev. B 85, 155301 (2012). [106] S. Wolgast et al., Low temperature surface conduction in the Kondo insulator SmB6 . Phys. Rev. B 88, 180405(R) (2013). [107] D. J. Kim, J. Xia & Z. Fisk, Topological surface state in the Kondo insulator samarium hexaboride. Nature Mater. 13, 466-470 (2014). [108] D. Hsieh et al., Nonlinear Optical Probe of Tunable Surface Electrons on a Topological Insulator. Phys. Rev. Lett. 106, 057401 (2011). [109] J. N. Hancock et al., Surface State Charge Dynamics of a High-Mobility ThreeDimensional Topological Insulator. Phys. Rev. Lett. 107, 136803 (2011). BIBLIOGRAPHY [110] J. A. Sobota et al., Ultrafast Optical Excitation of a Persistent Surface-State Population in the Topological Insulator Bi2 Se3 . Phys. Rev. Lett. 108, 117403 (2012). [111] Y. H. Wang et al., Measurement of Intrinsic Dirac Fermion Cooling on the Surface of the Topological Insulator Bi2 Se3 Using Time-Resolved and AngleResolved Photoemission Spectroscopy. Phys. Rev. Lett. 109, 127401 (2012). [112] A. A. Schafgans et al., Landau level spectroscopy of surface states in the topological insulator Bi0.91 Sb0.09 via magneto-optics. Phys. Rev. B 85, 195440 (2012). [113] J. W. McIver et al., Control over topological insulator photocurrents with light polarization. Nature Nanotechnology 7, 96-100 (2012). [114] R. Valdés Aguilar et al., Terahertz Response and Colossal Kerr Rotation from the Surface States of the Topological Insulator Bi2 Se3 . Phys. Rev. Lett. 108, 087403 (2012). [115] L. Wu et al., A sudden collapse in the transport lifetime across the topological phase transition in (Bi1−x Inx )2 Se3 . Nature Phys. 9, 410-414 (2013). [116] L. Fu, Topological Crystalline Insulators. Phys. Rev. Lett. 106, 106802 (2011). [117] H. Hsieh et al., Topological Crystalline Insulators in the SnTe Material Class. Nature Commun. 3, 982 (2012). [118] M. Dzero et al., Topological Kondo Insulators. Phys. Rev. Lett. 104, 106408 (2010). [119] X. Wan et al., Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011). 218 BIBLIOGRAPHY [120] S. Murakami, Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase. New. J. Phys. 9, 356 (2007). [121] S. M. Young et al., Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012). [122] Z. Wang et al., Three-dimensional Dirac semimetal and quantum transport in Cd3 As2 . Phys. Rev. B 88, 125427 (2013). [123] Z. Wang et al., Dirac semimetal and topological phase transitions in A3 Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012). [124] B.-J. Yang & N. Nagaosa Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Preprint at http://arXiv:1404.0754 (2014). [125] L. Fu & C. L. Kane, Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 100, 096407 (2008). [126] X.-L. Qi, T. L. Hughes & S.-C. Zhang, Topological field theory of TR invariant insulators. Phys. Rev. B 78, 195424 (2008). [127] R. Yu et al., Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61-64 (2010). [128] T. Grover, D. N. Sheng & A. Vishwanath, Emergent Space-Time Supersymmetry at the Boundary of a Topological Phase. Science 344, 280-283 (2014). [129] Z.-C. Gu & X.-G. Wen, Tensor-Entanglement-Filtering Renormalization Approach and Symmetry Protected Topological Order. Phys. Rev. B 80, 155131 (2009). [130] N. Regnault & B. Andrei Bernevig, Fractional Chern Insulator. Phys. Rev. X 1, 021014 (2011). BIBLIOGRAPHY [131] M. Levin & A. Stern, Fractional topological insulators. Phys. Rev. Lett. 103, 196803 (2009). [132] Y. Sun et al., Rocksalt SnS and SnSe: Native topological crystalline insulators. Phys. Rev. B 88, 235122 (2013). [133] A. Damascelli, Z. Hussain & Z-.X. Shen, Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473-541 (2003). [134] S. Hufner, Photoelectron Spectroscopy. Springer, Berlin, 1995. [135] M. Hoesch et al., Spin structure of the Shockley surface state on Au(111). Phys. Rev. B 69, 241401(R) (2004). [136] D. Hsieh, Spin-resolved spectroscopic studies of topologically ordered materials. PhD dissertation, Princeton University. [137] F. U. Hillebrecht et al., High-efficiency spin polarimetry by very-low-energy electron scattering from Fe(100) for spin-resolved photoemission. Rev. Sci. Instrum. 73, 1229-1234 (2002). [138] T. Okuda et al., Efficient spin resolved spectroscopy observation machine at Hiroshima Synchrotron Radiation Center. Rev. Sci. Instrum. 82, 103302 (2011). [139] P. Goswami & S. Chakravarty, Quantum Criticality between Topological and Band Insulators in 3+1 Dimensions. Phys. Rev. Lett. 107, 196803 (2011). [140] G. Cho et al., Possible topological phases of bulk magnetically doped Bi2 Se3 : turning a topological band insulator into the Weyl semimetal. Preprint at http://arXiv:1110.1939 (2011). [141] D. Bulmash, C.-X. Liu & X.-L. Qi, Prediction of a Weyl Semimetal in Hg1−x−y Cdx Mny Te. Phys. Rev. B 89, 081106 (2014). 220 BIBLIOGRAPHY [142] C. Wang, A. C. Potter & T. Senthil, Classification of Interacting Electronic Topological Insulators in Three Dimensions. Science 343, 629-631 (2014). [143] V. D.Kulibaba, Some properties of Sb2 Se3 condensates, Inorg. Mater. 24, 15231526 (1988). [144] B. Yan et al., Theoretical prediction of topological insulators in thallium-based III-V-VI2 ternary chalcogenides. Euro. Phys. Lett. 90, 37002 (2010). [145] H. Lin et al., Single-Dirac-Cone Topological Surface States in the TlBiSe2 Class of Topological Semiconductors. Phys. Rev. Lett. 105, 036404 (2010). [146] K. Kuroda et al., Experimental Realization of a Three-Dimensional Topological Insulator Phase in Ternary Chalcogenide TlBiSe2 . Phys. Rev. Lett. 105, 146801 (2010). [147] T. Sato et al., Direct Evidence for the Dirac-Cone Topological Surface States in the Ternary Chalcogenide TlBiSe2 . Phys. Rev. Lett. 105, 136802 (2010). [148] Y. L. Chen et al., Single Dirac Cone Topological Surface State and Unusual Thermoelectric Property of Compounds from a New Topological Insulator Family. Phys. Rev. Lett. 105, 266401 (2010). [149] C.-X. Liu, P. Ye & X.-L. Qi, Chiral gauge field and axial anomaly in a Weyl semi-metal. Phys. Rev. B 87, 235306 (2013). [150] N. H. Lindner, G. Refael & V. Galitski, Floquet topological insulator in semiconductor quantum wells. Nature Phys. 7, 490-495 (2011). [151] L. Fu & E. Berg, Odd-Parity Topological Superconductors: Theory and Application to Cux Bi2 Se3 . Phys. Rev. Lett. 105, 097001 (2010). BIBLIOGRAPHY [152] I. Zeljkovic et al., Transformation of Dirac Surface States across the Quantum Phase Transition in a Topological Crystalline Insulator. Preprint at http://arXiv:1403.4906 (2014). [153] C. Fang et al., Theory of quasiparticle interference in mirror-symmetric twodimensional systems and its application to surface states of topological crystalline insulators. Phys. Rev. B 88, 125141 (2013). [154] C. Fang, M. J. Gilbert & B. A. Bernevig, Large-Chern-Number Quantum Anomalous Hall Effect in Thin-Film Topological Crystalline Insulators. Phys. Rev. Lett. 112, 046801 (2014). [155] J. Liu et al., Spin-filtered edge states with an electrically tunable gap in a twodimensional topological crystalline insulator. Nature Mater. 13, 178-183 (2014). [156] E. Tang & L. Fu, Strain-Induced Helical Flat Band and Interface Superconductivity in Topological Crystalline Insulators. Preprint at http://arXiv:1403.7523 (2014). [157] A. Gyenis et al., Quasiparticle interference on the surface of the topological crystalline insulator Pb1−x Snx Se.Phys. Rev. B 88, 125414 (2013). [158] T. Liang et al., Evidence for massive bulk Dirac fermions in Pb1−x Snx Se from Nernst and thermopower experiments. Nature Commun. 4, 2696 (2013). [159] B. M. Wojek et al., Spin-polarized (001) surface states of the topological crystalline insulator Pb0.73 Sn0.27 Se. Phys. Rev. B 87, 115106 (2013). [160] S. Safaei, P. Kacman & R. Buczko, Topological crystalline insulator (Pb,Sn)Te: Surface states and their spin polarization. Phys. Rev. B 88, 045305 (2013). [161] A. A. Taskin et al., Topological surface transport in epitaxial SnTe thin films grown on Bi2 Te3 . Phys. Rev. Lett. 89, 121302(R) (2014). 222 BIBLIOGRAPHY [162] Y. Tanaka et al., Two types of Dirac-cone surface states on (111) surface of topological crystalline insulator SnTe. Preprint at http://arXiv:1312.2803 (2013). [163] C. M. Polley et al., Observation of topological crystalline insulator surface states on (111)-oriented Pb1−x Snx Se films. Phys. Rev. Lett. 89, 075317 (2014). [164] I. Pletikosić, G. D. Gu & T. Valla, Inducing a Lifshitz Transition by Extrinsic Doping of Surface Bands in the Topological Crystalline Insulator Pb1−x Snx Se. Phys. Rev. Lett. 112, 146403 (2014). [165] G. Balakrishnan, L. Bawden, S. Cavendish & M. R. Lees, Superconducting properties of the In-substituted topological crystalline insulator SnTe. Phys. Rev. B 87, 140507(R) (2013). [166] T. Sato et al., Fermiology of the Strongly Spin-Orbit Coupled Superconductor Sn1−x Inx Te: Implications for Topological Superconductivity. Phys. Rev. Lett. 110, 206804 (2013). [167] R. D. Zhang et al., Optimizing the superconducting transition temperature and upper critical field of Sn1−x Inx Te. Phys. Rev. Lett. 88 020505(R) (2013). [168] L. P. He et al., Full superconducting gap in the doped topological crystalline insulator Sn0.6 In0.4 Te. Phys. Rev. Lett. 88, 014523 (2013). [169] M. Novak et al., Unusual nature of fully gapped superconductivity in In-doped SnTe. Phys. Rev. B 88, 140502(R) (2013). [170] J. C. Y. Teo, L. Fu & C. L. Kane, Surface states and topological invariants in three-dimensional topological insulators: Application to Bi1−x Sbx . Phys. Rev. B 78, 045426 (2008). BIBLIOGRAPHY [171] A. Alexandradinata, C. Fang, M. J. Gilbert & B. A. Bernevig, Spin-Orbit-Free Topological Insulators without Time-Reversal Symmetry. Phys. Rev. Lett. 113, 116403 (2014). [172] J. O. Dimmock & G. B. Wright, Band Edge Structure of PbS, PbSe, and PbTe. Phys. Rev. 135, 821 (1964). [173] J.O. Dimmock, I. Melngailis & A.J. Strauss, Band structure and laser action in Pbx Sn1−x Te. Phys. Rev. Lett. 16, 1193 (1966). [174] X. Gao & M. S. Daw, Investigation of band inversion in (Pb,Sn)Te alloys using ab initio calculations. Phy. Rev. B 77, 033103 (2008). [175] O. A. Pankratov, S. V. Pakhomov & B. A. Volkov, Supersymmetry in heterojunctions: Band-inverting contact on the basis of Pb1−x Snx Te and Hg1−x Cdx Te. Solid State Commun. 61, 93-96 (1987). [176] G. Li et al., Observation of van Hove singularities in twisted graphene layers. Nature Phys. 6, 109-113 (2010). [177] J. Nilsson et al., Electron-electron interactions and the phase diagram of a graphene bilayer. Phys. Rev. B 73, 214418 (2006) . [178] R. Nandkishore, R. L. S Levitov & A. V. Chubukov, Chiral superconductivity from repulsive interactions in doped graphene. Nature Phys. 8, 158-163 (2012). [179] S.Lipinski & D. Krychowski, Kondo effect near the van Hove singularity in biased bilayer graphene. Preprint at http://arXiv:1206.4455 (2013). [180] L. A. Ponomarenko et al., Cloning of Dirac fermions in graphene superlattices. Nature 497, 594-597 (2013). [181] R. C. Dean et al., Hofstadter’s butterfly in moire superlattices: A fractal quantum Hall effect. Nature 497, 598-602 (2013). 224 BIBLIOGRAPHY [182] A. Okazaki & I. Ueda, The Crystal Structure of Stannous Selenide SnSe. J. Phys. Soc. Japan 11, 470-470 (1956). [183] A. A. Volykhov et. al., Phase relations between germanium, tin, and lead chalcogenides in pseudobinary systems containing orthorhombic phases. Inorganic Materials 44, 345-356 (2008). [184] W. Albers et. al., Preparation and properties of mixed crystals SnS(1−x) Sex . J. Phys. Chem. Solids 23, 215-220 (1962). [185] F. D. M. Haldane, Attachment of Surface “Fermi Arc” to the Bulk Fermi Surface: “Fermi-Level Plumbing” in Topological Metals. Preprint at http://arXiv:1401.0529 (2014). [186] A. C. Potter, I. Kimchi & A. Vishwanath, Quantum Oscillations from Surface Fermi-Arcs in Weyl and Dirac Semi-Metals. Preprint at http://arXiv:1402.6342 (2014). [187] P. Hosur, Friedel oscillations due to Fermi arcs in Weyl semimetals. Phys. Rev. B 86, 195102 (2012). [188] G. B. Halasz & L. Balents, Time-reversal invariant realization of the Weyl semimetal phase. Phys. Rev. B 85, 035103 (2012). [189] M. Koshino & T. Ando, Anomalous orbital magnetism in Dirac-electron systems: Role of pseudospin paramagnetism. Phys. Rev. B 81, 195431 (2010). [190] T. Ojanen, Helical Fermi arcs and surface states in time-reversal invariant Weyl semimetals. Phys. Rev. B 87, 245112 (2013). [191] S.-K. Jian, Y.-F. Jiang & H. Yao, Emergent space-time supersymmetry in 3+1D Weyl and 2+1D Dirac semimetals. Preprint at http://arXiv:1407.4497 (2014). BIBLIOGRAPHY [192] T. Meng & L. Balents, Weyl superconductors. Phys. Rev. B 86, 054504 (2012). [193] A. A. Burkov, M. D. Hook & Leon Balents, Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011). [194] J.-P. Jay-Gerin et al., The electron mobility and the static dielectric constant of Cd3 As2 at 4.2 K, Solid State Commun. 21, 771-774 (1977). [195] L. Zdanowicz et al., Shubnikov-de Hass effect in amorphous Cd3 As2 in Applications of High Magnetic Fields in Semiconductor Physics. Lect. Notes Phys., 177, 386-395 (1983). [196] G. A. Steigmann & J. Goodyear, The Crystal Structure of Cd3 As2 . Acta Cryst. B 24, 1062-1067 (1968). [197] B. D. Plenkiewicz & P. Plenkiewicz, Inverted band structure of Cd3 As2 . Physica Status Solidi(b) 94, K57-K60 (2006). [198] A. Bostwick et al., Quasiparticle dynamics in graphene. Nature Phys. 3, 36-40 (2007). [199] T. B. Massalski, Binary alloy phase diagrams (ASM, Materials Park, 1990). [200] D. M. King et al., Observation of a saddle-point singularity in Bi2 (Sr0.97 Pr0.03 )2 CuO6+δ and its implications for normal and superconducting state properties. Phys. Rev. Lett. 73, 3298 (1994). [201] C. Liu et al., Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nature Phys. 6, 419-423 (2010). [202] X. Chen, Z.-C. Gu, Z.-X. Liu & X.-G. Wen, Symmetry protected topological orders and the group cohomology of their symmetry group. Phys. Rev. B 87, 155114 (2013). 226 BIBLIOGRAPHY [203] G. Aeppli & Z. Fisk. Kondo insulators. Comm. Condens. Matter Phys. 16, 155-165 (1992). [204] P. Riseborough, Heavy fermion semiconductors. Adv. Phys. 49, 257-320 (2000). [205] P. Coleman, Handbook of Magnetism and Advanced Magnetic Materials 1, 95148 (2007). [206] T. Takimoto, SmB6 : a promising candidate for a topological insulator. J. Phys. Soc. Jpn. 80, 123710 (2011). [207] F. Lu et al., Correlated topological insulators with mixed valence. Phys. Rev. Lett. 110, 096401 (2013). [208] A. Menth et al., Magnetic and semiconducting properties of SmB6 . Phys. Rev. Lett. 22, 295-297 (1969). [209] J. W. Allen et al., Large low-temperature Hall effect and resistivity in mixedvalent SmB6 . Phys. Rev. B 20, 4807-4813 (1979). [210] J. C. Cooley et al., SmB6 : Kondo insulator or exotic metal? Phys. Rev. Lett. 74, 1629-1632 (1995). [211] M. Miyazaki et al., Momentum-dependent hybridization gap and dispersive ingap state of the Kondo semiconductor SmB6 . Phys. Rev. B 86, 075105 (2012). [212] J. D. Denlinger et al., Advances in photoemission spectroscopy of f-electron materials. Physica B 281, 716-722 (2000). [213] S. Kimura et al., Low-energy optical excitation in rare-earth hexaborides. Phys. Rev. B 50, 1406-1414 (1994). [214] T. Nanba et al., Gap state of SmB6 . Physica B 186, 440-443 (1993). BIBLIOGRAPHY [215] P. Nyhus et al., Low-energy excitations of the correlation-gap insulator SmB6 : A light-scattering study. Phys. Rev. B 55, 12488-12496 (1997). [216] P. A. Alekseev et al., Magnetic excitations in SmB6 single crystals. Physica B 186, 384-386 (1993). [217] K. Flachbart et al., Energy gap of intermediate-valent SmB6 studied by pointcontact spectroscopy. Phy. Rev. B 64, 085104 (2001). [218] J. Botimer et al., Robust surface hall effect and nonlocal transport in SmB6 : indication for an ideal topological insulator. Sci. Rep. 3, 3150 (2013). [219] X. Zhang et al., Hybridization, inter-ion correlation, and surface states in the Kondo insulator SmB6 . Phys. Rev. X 3, 011011 (2013). [220] V. N. Antonov et al., Electronic Structure of Strongly Correlated Systems. Adv. Con. Mat. Phys. 2011, 1-107 (2011). [221] J. M. Tarascon et al., Magnetic and transport properties of pure and carbondoped divalent RE hexaboride single crystals. Appl. Phys. Lett. 100, 253115 (2012). [222] H. Weng et al., Topological Crystalline Kondo Insulator in Mixed Valence Ytterbium Borides. Phys. Rev. Lett. 112, 016403 (2014). [223] A. M. Essin, J. E. Moore & D. Vanderbilt, Magnetoelectric Polarizability and Axion Electrodynamics in Crystalline Insulators. Phys. Rev. Lett. 102, 146805 (2009). [224] R. Li, J. Wang, X.-L. Qi & S.-C. Zhang, Dynamical axion field in topological magnetic insulators. Nature Phys. 6, 284-288 (2010). 228 BIBLIOGRAPHY [225] X.-L. Qi, T. L. Hughes, S. Raghu & S.-C. Zhang. Time-Reversal-Invariant Topological Superconductors and Superfluids in Two and Three Dimensions. Phys. Rev. Lett. 102, 187001 (2009). [226] I. Garate & M. Franz, Inverse spin-galvanic effect in the interface between a topological insulator and a ferromagnet. Phys. Rev. Lett. 104, 146802 (2010). [227] R. Nakajima et al., Electron-yield saturation effects in L-edge x-ray magnetic circular dichroism spectra of Fe, Co, and Ni. Phys. Rev. B 59, 6421-6429 (1999). [228] K. W. Edmonds et al., Ferromagnetic moment and antiferromagnetic coupling in (Ga,Mn)As thin films. Phys. Rev. B 71, 064418 (2005). [229] L. Fu, Hexagonal Warping Effects in the Surface States of the Topological Insulator Bi2 Te3 . Phys. Rev. Lett. 103, 266801 (2009). [230] H.-Z. Lu, J. R. Shi & S.-Q. Shen, Competition between Weak Localization and Antilocalization in Topological Surface States. Phys. Rev. Lett. 107, 076801 (2011). [231] R. Nandkishore, L. S. Levitov & A. V. Chubukov, Chiral superconductivity from repulsive interactions in doped graphene. Nature Phys. 8, 158-163 (2012). [232] A. C. Potter & P. A. Lee, Engineering a p + ip superconductor: Comparison of topological insulator and Rashba spin-orbit-coupled materials. Phys. Rev. B 83, 184520 (2011). [233] J. D. Sau et al., A generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 (2010). [234] P. Hosur et al., Majorana Modes at the Ends of Superconductor Vortices in Doped Topological Insulators. Phys. Rev. Lett. 107, 097001 (2011). BIBLIOGRAPHY [235] S. Sasaki et al., Topological Superconductivity in Cux Bi2 Se3 . Phys. Rev. Lett. 107, 217001 (2011). [236] D. Zhang et al., Superconducting proximity effect and possible evidence for Pearl vortices in a candidate topological insulator. Phys. Rev. B 84, 165120 (2011). [237] G. Koren et al., Proximity-induced superconductivity in topological Bi2 Te2 Se and Bi2 Se3 films: Robust zero-energy bound state possibly due to Majorana fermions. Phys. Rev. B 84, 224521 (2011). [238] F. Qu et al., Strong Superconducting Proximity Effect in Pb-Bi2 Te3 Hybrid Structures. Sci. Rep. 2, 339 (2012). [239] S. Cho et al., Symmetry Protected Josephson Supercurrents in ThreeDimensional Topological Insulators. Nature Commun. 4, 1689 (2013). [240] J. R. Williams et al., Unconventional Josephson Effect in Hybrid Superconductor-Topological Insulator Devices. Phys. Rev. Lett. 109, 056803 (2012). [241] J.-P. Xu et al., Artificial Topological Superconductor by the Proximity Effect. Phys. Rev. Lett. 112, 217001 (2014). [242] M.-X. Wang et al., The Coexistence of Superconductivity and Topological Order in the Bi2 Se3 Thin Films. Science 336, 52-55 (2012). [243] V. Mourik et al., Signatures of Majorana Fermions in Hybrid SuperconductorSemiconductor Nanowire Devices. Science 336, 1003-1007 (2012). [244] J. Liu et al., Zero-Bias Peaks in the Tunneling Conductance of Spin-OrbitCoupled Superconducting Wires with and without Majorana End-States. Phys. Rev. Lett. 109, 267002 (2012). 230 BIBLIOGRAPHY [245] D. Roy, N. Bondyopadhaya & S. Tewari, Topologically trivial zero-bias conductance peak in semiconductor Majorana wires from boundary effects. Phys. Rev. B 88, 020502(R) (2013). [246] H. O. H. Churchill et al., Superconductor-Nanowire Devices from Tunneling to the Multichannel Regime: Zero-Bias Oscillations and Magnetoconductance Crossover. Phys. Rev. B 87, 241401(R) (2013). [247] E. J. H. Lee et al., Spin-resolved Andreev levels and parity crossings in hybrid superconductor-semiconductor nanostructures. Nature nanotech. 9, 79-84 (2014). [248] K. Okazaki et al., Octet-Line Node Structure of Superconducting Order Parameter in KFe2 As2 . Science 337, 1314-1317 (2012). [249] G. Blonder, M. Tinkham & T. Klapwijk, Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B 25, 4515-4532 (1982). [250] P. C. van Son, H. van Kempen & P. Wyder, New method to study the proximity effect at the normal-metal-superconductor interface. Phys. Rev. Lett. 59, 22262228 (1987). [251] D. Heslinga et al., Observation of double-gap-edge Andreev reflection at Si/Nb interfaces by point-contact spectroscopy. Phys. Rev. B 49, 10484-10494 (1994). [252] E. Wang et al., Fully gapped topological surface states in Bi2 Se3 films induced by a d-wave high-temperature superconductor. Nature Phys. 9, 621-625 (2013). Appendices 232 A List of Publications Relevant to This Thesis A. Principal Publications 1. Su-Yang Xu et al., Fermi Arc Surface States in a Topological Metal: A New Type of 2D Electron Gas. DOI:10.1126/science.1256742 Science (2014). 2. Su-Yang Xu et al., Topological Phase Transition and Texture Inversion in a Tunable Topological Insulator. Science 332, 560-564 (2011). 3. Su-Yang Xu et al., Momentum space imaging of Cooper pairing in a half Dirac gas topological superconductor. Nature Phys. doi:10.1038/nphys3139 (2014). 4. Su-Yang Xu et al., Hedgehog spin texture and Berrys phase tuning in a magnetic topological insulator. Nature Phys. 8, 616-622 (2012). 5. L. A. Wray, Su-Yang Xu et al., A topological insulator surface under strong Coulomb, magnetic and disorder perturbations. Nature Phys. 7, 32-37 (2011). 6. L. A. Wray, Su-Yang Xu et al., Observation of topological order in a superconducting doped topological insulator. Nature Phys. 6, 855-859 (2010). 7. Su-Yang Xu et al., Observation of a topological crystalline insulator phase and topological phase transition in Pb1−x Snx Te. Nature Commun. 3, 1192 (2012). 8. Su-Yang Xu et al., Su-Yang Xu et al., Unconventional transformation of spin-Dirac phase across a topological quantum phase transition. in review in Nature Commun. (2014). 9. M. Neupane*, Su-Yang Xu* et al., Observation of a topological 3D Dirac semimetal phase in high-mobility Cd3 As2 . Nature Commun. 5, 4786 (2014). 10. H. Lin, L. A. Wray, Y. Xia, Su-Yang Xu et al., Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nature Mater. 9, 546-549 (2010). 11. Su-Yang Xu et al., Fermi-level electronic structure of a topological-insulator/cupratesuperconductor based heterostructure in the superconducting proximity effect regime. Phys. Rev. B, 90 085128 (2014). B. Full List 1. Su-Yang Xu et al., Fermi Arc Surface States in a Topological Metal: A New Type of 2D Electron Gas. DOI:10.1126/science.1256742 in Science (2014). 2. Su-Yang Xu et al., Su-Yang Xu et al., Unconventional transformation of spin-Dirac phase across a topological quantum phase transition. in review in Nature Commun. (2014). 3. Su-Yang Xu et al., Momentum space imaging of Cooper pairing in a half Dirac gas topological superconductor. Nature Phys. doi:10.1038/nphys3139 (2014). 4. M. Z. Hasan, Su-Yang Xu, M. Neupane et al., Topological Insulators, Topological Crystalline Insulators, and Topological Kondo Insulators. Preprint at http://arXiv:1406.1040 (Invited Book Chapter) (2014). 5. M. Neupane*, Su-Yang Xu* et al., Observation of non-Kondo-like electronic structure in strongly correlated electron system YbB6 . Preprint at http://arXiv:1404.6814 (2014). 6. M. Neupane, A. Richardella, J. Snchez-Barriga, Su-Yang Xu et al., Observation of Quantum-Tunneling Modulated Spin Texture in Ultrathin Topological Insulator Bi2 Se3 Films. Nature Commun. 5, 3841 (2014). 7. Anjan A. Reijnders, Y. Tian, L. J. Sandilands, G. Pohl, I. D. Kivlichan, S. Y. Frank Zhao, S. Jia, M. E. Charles, R.J. Cava, Nasser Alidoust, Su-Yang Xu et al., Optical evidence of surface state suppression in Bi based topological insulators. Phys. Rev. B 89, 075138 (2014). 8. Chang Liu*, Su-Yang Xu* et al., Spin correlated electronic state on the surface of a spin-orbit Mott system (Layered Iridates). Phys. Rev. B 90, 045127 (2014). 9. Su-Yang Xu et al., Fermi-level electronic structure of a topological-insulator/cupratesuperconductor based heterostructure in the superconducting proximity effect regime. Phys. Rev. B, 90 085128 (2014). 234 10. M. Neupane*, Su-Yang Xu* et al., Saddle point singularity and topological phase diagram in a tunable topological crystalline insulator (TCI). Preprint at http://arXiv:1403.1560 (2014). 11. M. Neupane*, Su-Yang Xu* et al., Observation of a topological 3D Dirac semimetal phase in high-mobility Cd3 As2 . Nature Commun. 5, 4786 (2014). 12. N. Alidoust, G. Bian, Su-Yang Xu et al., Observation of monolayer valence band spin-orbit effect and induced quantum well states (QWS) in MoX2 . Nature Commun. 5, 4673 (2014). 13. Su-Yang Xu et al., Observation of a bulk 3D Dirac multiplet, Lifshitz transition, and nestled spin states in Na3 Bi. Preprint at http://arXiv:1312.7624 (2013). 14. M. Z. Hasan, Su-Yang Xu, D. Hsieh, L. A. Wray & Y. Xia, Topological Surface States: A New Type of 2D Electron Systems (Book chapter). in Topological Insulators edited by M. Franz and L. Molenkamp (Elsevier, Oxford 2013). 15. M. Neupane, S. Basak, N. Alidoust, Su-Yang Xu et al., Oscillatory surface dichroism of an insulating topological insulator Bi2 Te2 Se. Phys. Rev. B 88, 165129 (2013). 16. Y Okada, M. Serbyn, H. Lin, D. Walkup, W. Zhou, C. Dhital, M. Neupane, Su-Yag Xu et al., Observation of Dirac node formation and mass acquisition in a topological crystalline insulator. Science 341, 1496-1499 (2013). 17. M. Neupane, N. Alidoust, Su-Yang Xu et al., Surface electronic structure of a topological Kondo insulator candidate SmB6 : insights from high-resolution ARPES. Nature Commun. 4, 2991 (2013). 18. L. A. Wray, Su-Yang Xu et al., Chemically gated electronic structure of a superconducting doped topological insulator system. J. Phys.: Conf. Ser. 449 012037 (2013). 19. C. Fang, M. J. Gilbert, Su-Yang Xu, B. A. Bernevig, M. Z. Hasan, Theory of quasiparticle interference in mirror symmetric 2D systems and its application to surface states of topological crystalline insulators. Phys. Rev. B 88, 125141 (2013). 20. H. Lin, Tanmoy Das, L. A. Wray, Su-Yang Xu et al., An isolated Dirac cone on the surface of ternary tetradymite-like topological insulators. New J. of Phys. 13, 095005 (2011). 21. Y. J. Wang, W.-F. Tsai, H. Lin, Su-Yang Xu et al., Nontrivial spin texture of the coaxial Dirac cones on the surface of topological crystalline insulator SnTe. Phys. Rev. B 87, 235317 (2013). 22. Hsin Lin, Tanmoy Das, Yung Jui Wang, L. A. Wray, Su-Yang Xu et al., Adiabatic transformation as a search tool for new topological insulators: Distorted ternary Li2 AgSb-class semiconductors and related compounds. Phys. Rev. B 87, 121202 (2013). 23. Su-Yang Xu et al., Observation of a topological crystalline insulator phase and topological phase transition in Pb1−x Snx Te. Nature Commun. 3, 1192 (2012). 24. Su-Yang Xu et al., Hedgehog spin texture and Berrys phase tuning in a magnetic topological insulator. Nature Phys. 8, 616-622 (2012). 25. M. Brahlek, N. Bansal, N. Koirala, Su-Yang Xu et al., Topological-Metal to Band-Insulator Transition in (Bi1−x Inx )2 Se3 Thin Films. Phys. Rev. Lett. 109, 186403 (2012). 26. M. Neupane, Su-Yang Xu et al., Topological surface states and Dirac point tuning in ternary topological insulators. Phys. Rev. B 85, 235406 (2012). 27. D. Zhang, A. Richardella, D. W. Rench, Su-Yang Xu et al., Interplay between ferromagnetism, surface states, and quantum corrections in a magnetically doped topological insulator. Phys. Rev. B 86, 205127 (2012). 28. Su-Yang Xu et al., Dirac point spectral weight suppression and surface ”gaps” in nonmagnetic and magnetic topological insulators. Preprint at http://arXiv:1206.0278 (2012). 29. Su-Yang Xu et al., Anomalous spin-momentum locked two-dimensional 236 states in the vicinity of a topological phase transition. Preprint at http://arXiv:1204.6518 (2012). 30. Helin Cao, Su-Yang Xu et al., Structural and electronic properties of highly doped topological insulator Bi2 Se3 crystals. physica status solidi 7, 133-135 (2012). 31. M. Neupane, C. Liu, Su-Yang Xu et al., Fermi-surface topology and lowlying electronic structure of the iron-based superconductor Ca10 (Pt3 As8 )(Fe2 As2 )5 . Phys. Rev. B 85, 094510 (2012). 32. H. Ji, J. M. Allred, N. Ni, J. Tao, M. Neupane, A. Wray, Su-Yang Xu et al., Bulk intergrowth of a topological insulator with a room-temperature ferromagnet. Phys. Rev. B 85, 165313 (2012). 33. Su-Yang Xu et al., Topological Phase Transition and Texture Inversion in a Tunable Topological Insulator. Science 332, 560-564 (2011). 34. L. A. Wray, Su-Yang Xu et al., A topological insulator surface under strong Coulomb, magnetic and disorder perturbations. Nature Phys. 7, 32-37 (2011). 35. L. A. Wray, Su-Yang Xu et al., Spin-orbital ground states of superconducting doped topological insulators: A Majorana platform. Phys. Rev. B 83, 224516 (2011). 36. S. Basak, H. Lin, L. A. Wray, Su-Yang Xu et al., Spin texture on the warped Dirac-cone surface states in topological insulators. Phys. Rev. B 84, 121401(R) (2011). 37. Su-Yang Xu et al., Realization of an isolated Dirac node and strongly modulated Spin Texture in the topological insulator Bi2 Te3 . Preprint at http://arXiv:1101.3985 (2011). 38. M. Z. Hasan, D. Hsieh, Y. Xia, L. A. Wray, Su-Yang Xu, C. L. Kane, A new experimental approach for the exploration of topological quantum phenomena: Topological Insulators and Superconductors. Preprint at http://arXiv:1105.0396(2011). (Review article). 39. Su-Yang Xu et al., Discovery of several large families of Topological Insu- lator classes with backscattering-suppressed spin-polarized single-Dirac-cone on the surface. Preprint at http:// arXiv:1007.5111 (2010). 40. L. A. Wray, Su-Yang Xu et al., Observation of topological order in a superconducting doped topological insulator. Nature Phys. 6, 855-859 (2010). 41. H. Lin, L. A. Wray, Y. Xia, Su-Yang Xu et al., Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nature Mater. 9, 546-549 (2010). 42. Y. S. Hor, P. Roushan, H. Beidenkopf, J. Seo, D. Qu, J. G. Checkelsky, L. A. Wray, D. Hsieh, Y. Xia, Su-Yang Xu, Development of ferromagnetism in the doped topological insulator Bi2−x Mnx Te3 . Phys. Rev. B 81, 195203 (2010). 43. W. Al-Sawai, H. Lin, R. S. Markiewicz, L. A. Wray, Y. Xia, Su-Yang Xu et al., Topological electronic structure in half-Heusler topological insulators. Phys. Rev. B 82, 125208 (2010). 44. M. D. Schroer, Su-Yang Xu et al.,Development and operation of researchscale IIIV nanowire growth reactors. Rev. Sci. Instrum. 81, 023903 (2010). 238