Download - Lorentz Center

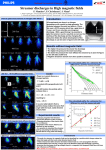
Modeling of streamer breakdown
of short non-uniform air gaps
G.V. Naidis
Institute for High Temperatures
Russian Academy of Sciences
Moscow, Russia
Lorentz Center workshop, Leiden, May 2005
Streamer-to-spark transition is considered in a
rod-to-plane gap with the length d = 1 cm in air
at pressure 1 bar and temperature 300 K
Two stages of the transition are simulated:
1) Streamer propagation inside the gap. At U/d > 5
kV/cm streamer bridges the gap, forming a plasma
channel with relatively low electrical conductivity
(τpropagation ~ 10 ns)
2) Evolution of plasma in the channel, governed by
kinetic and gas dynamic processes
(τbreakdown ~ 102-104 ns, depending on U)
2
Mechanisms resulting in streamer-to-spark
transition:
1) Thermal mechanism: a lowering of the gas density N inside
the channel due to expansion of the heated plasma (Marode
e.a.1979,1985; Bayle e.a.1985).
This factor is ineffective at τbreakdown « τexpansion
= R/Csound ~ 6x102 ns (for R = 0.02 cm).
2) Kinetic mechanism: accumulation of active particles changing
the ionization balance (Rodriguez e.a.1991; Eletskiy e.a.1991;
Lowke 1992; Aleksandrov, Bazelyan e.a.1998; Naidis 1999).
In the present work both factors are accounted for.
3
Simulation of positive streamer propagation
1) 2D model (with axial symmetry):
E  ,
,.
N j
t
 2  4π
 ( N j  j E)  F j  S j
2) 1.5D model, with constant streamer radius R,
electric field is calculated using the method of disks
Calculated streamer parameters:
R = 0.02-0.04 cm, Nec = (1.5-3.0)x1014 cm-3
4
Simulation of channel evolution after bridging the gap
Telegraph equations for the electric field E and current I :

I ( z, t )
  E ( z, t )  
,
z
( z , t )
,
I
( z, t )
 C
,
z
t
the capacity and electrical conductivity per unit length are
C
1
,
2 ln( d / R)
  πR 2e  j N j
j
Φ(0) Φ(d) = U - Ucathode, Ucathode = 0.2 kV.
5
Simulation of channel evolution after bridging the gap
Gas dynamic equations:
N 1 

(rNV )  0,
t r r
( NV ) 1 
1 
2

(rNV ) 
( NkT )  0,
t
r r
M r
ε v  ε v eq (T )
1  ( NkT )
1 1
NkT 

(rNkTV ) 
(rV )  ηT jE 
,
  1 t
  1 r r
r r
τ VT
ε v  ε v eq (T )
ε v 1 

(rε vV )  ηV jE 
t r r
τ VT
6
Simulation of channel evolution after bridging the gap
Kinetic equations for species N, O, NO, N2(A3Σ), N2(a'1Σ),
O2(a1Δ), ions O-, O2-, O3-, O2+, O4+, electrons:
N
( N j / N )
t
 Fj
.
(diffusion of species is neglected).
The density of energy input versus r is taken as
jE (r )  jE (0) exp( r 2 / R 2 )
7
Conditions of applicability of the model
1) Ions stay in the channel (positive charge does not change):
τbreakdown « τion drift = d/Vion ~ 4x104 ns
2) Diffusion of species may be neglected:
.
τbreakdown « τdiffusion = R2/6D
τbreakdown « τambipolar diffusion = R2/6Da
At R = 0.02 cm
τdiffusion ~ 4x105 ns, τambipolar diffusion ~ 3x104 ns
8
The electric field distributions along the channel
after bridging the gap at U = 19 kV
The distribution
becomes nearly
uniform along
the channel at
t ~ 102 ns
9
The electric current dependence on time
for various applied voltages
0D simulation at
E=(U-Ucathode)/d
gives the results in
agreement with
those of 1D model
(accounting for the
change of plasma
parameters along z)
1D (solid) and 0D (dashed) simulations at N = const
10
The electric current dependence on time
for various applied voltages
0D simulations: R = 0.02 cm, Ne0 = 2x1014 cm-3
11
The streamer-to-spark transition time
R = 0.02 (full) and 0.04 cm (broken), Ne0 = 2x1014 cm-3
12
The densities of neutral species
U = 19 kV (simulation at N = const)
13
The densities of charged species
U = 19 kV (simulation at N = const)
14
The rates of the processes of generation
and loss of electrons
Accumulation of
oxygen atoms leads
to the increase of
detachment rate,
resulting in the
change of sign of
the source term for
electrons
U = 19 kV (simulation at N = const)
15
Gas pressure at the streamer axis
for various applied voltages
At U = 18 kV
τbreakdown ~
τexpansion
(~ 103 ns)
16
Gas temperature at the streamer axis
for various applied voltages
17
Vibrational temperature of N2 molecules at the
streamer axis for various applied voltages
18
Gas density at the streamer axis
for various applied voltages
19
Reduced electric field at the streamer axis
for various applied voltages
20
Radial distributions of pressure at U = 18 kV
21
Radial distributions of gas temperature at U = 18 kV
22
Radial distributions of gas density at U = 18 kV
23
Radial distributions of gas velocity at U = 18 kV
24
The streamer-to-spark transition time
(the effect of initial electron density)
25
Effect of pressure variation
pd = 1 bar cm, pR = 0.02 bar cm, Ne0/p2 = 2x1014 cm-3 bar-2
26
Conclusions
1. Streamer breakdown of atmospheric-pressure air in gaps
with lengths d ~ 1cm at constant applied voltage U occurs
during one current pulse if U/d > 14 kV/cm.
In this case τbreakdown < 10-4 s.
2.
Streamer-to-spark transition at τbreakdown «10-6 s may be
described in approximation of constant gas density;
at τbreakdown »10-6 s it may be described in approximation
of constant pressure.
3.
Streamer breakdown is observed also at lower U/d. In this
case the breakdown is the result of a sequence of streamers,
propagating along the same path with frequencies
f < 104 Hz, each of these streamers changing slightly the
parameters of the medium (temperature, density, etc.).
27