Download Lecture4

Intermolecular
Forces:Electrostatics
•“Dielectrics
•Different classical electrostatic interactions
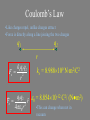
Coulomb’s Law
•Like charges repel, unlike charges attract
•Force is directly along a line joining the two charges
q1
q2
r
ke q1q2
Fe 
2
r
ke = 8.988109 Nm2/C2
-12 C2/ (N●m2)
q1q2

=
8.85410
0
ˆ
Fe 
r
2
4 0 r
•This can change when not in
vacuum
Dielectric
The dielectric constant tells us about how electric
fields are weakened due to mobility of dipoles.
If we place a charge in a media with
orientable/polarizable dipoles, the charge will be
“solvated” by the dipoles
Dielectric constants depend on mobility, size and
polarizability of dipoles
Not readily defined in a heterogenous flexible
medium!
Dielectric
In a homogenous material, a scale factor
In a complex material, poisson’s equation
Multiple charges
q3
r3
r1
q1
q2
r2
ke qi
V 
ri
We can handle multiple charges by considering
each on explicitly, or by a multipole expansion
Multipole expansion
(qualitatively)
When outside the charge distribution, consider a
set of charges as being a decomposition of a
monopole, a dipole { and higher order terms}
The monopole term is the net charge at the center
of the charges {often zero}
The dipole moment has its positive head at the
center of the positive changes, and its negative tail
at the center of the negative charges
Multipole expansion
The multipole expansion expands a potential in a
complete set of functions:


Pi (cos  )  

4 0 i 0
r
q

i
The significance is that we can study the different poles one by one, to
understand any charge distribution
Where might we have a significant dipole moment?
Where might we have a significant quadrapole moment?
Charge-Charge Interaction
r
q1q2
Ep 
2
4 0 r
0 = 8.85410-12 C2/ (N●m2)
When might we have charge-charge interactions?
Charge-Dipole Interaction
+

-
~
~
U   pE cos    p  E
p
+
E
 pq cos 
Ep 
4 0 r 2
What is ?
q1
4 0 r
2
rˆ
Dipole-Dipole Interaction
Since we have two different vectors, there are
two angles, and so the angular component
becomes complicated (see page20)
+
+
-
Ep 
p1 p 2 K
4 0 r 3
The angular component is interesting when
one has restricted motion, but otherwise only
the radial component is essential
Why is the angular component not interesting when one has
unrestricted motion?
When might restricted motion by interesting?
Npole-Mpole Interaction
In general, when there are different “poles”
interacting, the interaction energy has a rdependence that increases with increasing
order of the pole.
Ep 
1
r
m  n 1
The decreasing range of the electrostatics is
why higher order poles are less important,
especially in biomolecules, where they many
charges and dipoles {and quadrupoles around}
Induced Dipoles
When a molecule is placed in an external field,
the electron distribution is distorted
For example: when a molecule is placed in
water, the electric fields from the water
molecules will change the electron
distributions
pE
First approximation: with the polarizability
being the coefficient
Induced Dipoles
E
E
E2
E    p  dE   0  E  dE   0
2
0
0
•When the field is due to a charge
q2
E   0 4
2r (4 0 ) 2
•When the molecule has a scalar polarizability, and there is a dipole:
p0 2
E   0 6
2r (4 0 )2
Proportionality constant depends on
geometry if fixed; 2 if thermal motion
Induced Dipoles
E
1 2
r
6
Precise calculation requires high-quality QM
calc; form from radiation and matter
Included as part of vdW interactions
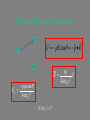
Thermal Averaging: ion-dipole
•Recall: At nonzero finite temperature, thermal energy can result in the
population of multiple states inside an ensemble
•What does this mean?
•We have to consider the statistical weight of each possible orientation
exp( E / kBT )  exp( pE cos  / kBT )
•Integrate to determine the mean value of p in the direction of the field:
p  p coth( pE / kBT )  kBT /( E)
Thermal Averaging: Results
•In the high T approximation:
•What is the high T approximation?
p  p 2 E / 3kBT
•When is the high T approximation realistic?
•This means that the mean Energy is
E   p2 E 2 / 3kBT
•This means that the mean Energy is:
E   p q /((4 0 ) 3kBTr )
2 2
2
4
Thermal Averaging: Dipole-Dipole
•In the high T approximation:
E  2 p12 p22 /((4 0 )2 3kBTr 6 )
•Note the range!
Why don’t I consider thermal motion with charge-charge interactions?
Hierarchy
Ion-ion
Charge-dipole
Dipole-dipole
Charge-molecule
Dipole-molecule
Fixed
Thermal
q1q2
r
qp
 2
r
q1q2
r
q2 p2

Tr 4
p12 p2 2

Tr 6
p1 p2
 3
r2
q
 4
r

 p 20
r6
Induced dipole-induced dipole

1 2 p 2 0
r6