Download chapter16

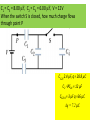
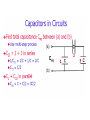
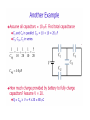
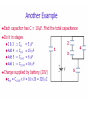
Summary
• More circuits
• Forces between
plates of a capacitor
• Dielectrics
• Energy and the
distinction about
constant Q or V.
C1 = 5μF, C2 = 10 μF, C3 = 2 μF
Calculate the equi. Capacitance.
a)
b)
c)
d)
6 μF
2 μF
4 μF
8 μF
a. Find the equivalent capacitance between points a and b.
b. What fraction of the total energy is stored in the 7 µF capacitor , if the circuit has been
charged by a 12 volt battery?
a. 12.92 µF
b. 46%
C1 = C3 = 8.00 μF, C2 = C4 = 6.00 μF, V = 12V
When the switch S is closed, how much charge flows
through point P
C123 2.4 µF, q = 28.8 µC
C2 C24 = 12 µF
C1234 = 3 µF q =36 µC
Δq = 7.2 µC
Question
• A parallel-plate capacitor has a plate area of 0.3m2
and a plate separation of 0.1mm. If the charge on
each plate has a magnitude of 5x10-6 C then the
force exerted by one plate on the other has a
magnitude of about:
• A. 0
B. 5N
E. 9 x 105 N
C. 9N
D. 1 x104 N
Question
• A parallel-plate capacitor
has a plate area of 0.3m2
and a plate separation of
0.1mm. If the charge on
each plate has a magnitude
of 5x10-6 C then the force
exerted by one plate on the
other has a magnitude of
about:
A. 0
B. 5N
C. 0. 9N
D. 1 x104 N
E. 9 x 105 N
F  qE 

q2
2 o A
5  10 
6 2
2  8.85  10
12
 0.3
 4.71N
The electric field = σ/2εo why?
C  o A/ d
C   Cair
q
-q
V
q'
V
-q'
q
V
-q
q
-q
V'
Capacitor with a dielectric
In 1837 Michael Faraday investigated what happens to the
capacitance C of a capacitor when the gap between the plates
is completely filled with an insulator (a.k.a. dielectric)
Faraday discovered that the new capacitance is given by :
C   Cair Here Cair is the capacitance before the insertion
of the dielectric between the plates. The factor  is known
as the dielectric constant of the material.
Faraday's experiment can be carried out in two ways:
1. With the voltage V across the plates remaining constant
In this case a battery remains connected to the plates .
This is shown in fig.a
2. With the charge q of the plates remaining constant.
In this case the plates are isolated from the battery
This is shown in fig.b
(25 - 15)
C   Cair
q
-q
V
q'
V
-q'
q
V
-q
q
-q
V'
Fig.a : Capacitor voltage V remains constant
This is bacause the battery remains connected to the plates
After the dielectric is inserted between the capacitor plates
the plate charge changes from q to q   q
q κq
q
The new capacitance C  
 κ  κCair
V
V
V
Fig.b : Capacitor charge q remains constant
This is bacause the plates are isolated
After the dielectric is inserted between the capacitor plates
V
the plate voltage changes from V to V  

The new capacitance C 
q
q
q

    Cair
V V /
V
(25 - 16)
C  o
A
 1   2 
2d
If the areas are A1 and A-A1.
C
Effect of a dielectric : C  κC
o
d
A 2  A1 (1   2 
C123 2.4 µF, q = 28.8 µC
C2 C24 = 12 µF
C1234 = 3 µF q =36 µC
The force on a filling dielectric as it is inserted between the
parallel plates of a capacitor.
C  C1  C2 
  1
dC
C
dx
L
o 
d
x


A1    1 

With the battery connected,
U1 = ½CV2
F 
x
  1
dU1
 U1
dx
L
L
L
With the battery disconnected,
U2 = Q2/2C
F 
  1
dU 2
 U2
dx
L
With the battery connected, since x is increasing downwards, a negative force is upwards,
pushing the dielectric away.
With the battery disconnected, the force is positive and pointed downwards, pulling in the
dielectric.
The force is proportional to (κ-1) and inversely to L.
To make the argument simple, we have omitted the fact that the field at the end includes the
fringe field which depends on distance between the plates. The result including fringe fields
is quantitatively different. See S. Margulies, American Journal of Physics, V. 52, p 515 (1984)
A question
What is the equivalent
capacitance between the
points A and B?
A.
B.
C.
D.
E.
1 μF
2 μF
4 μF
10μF
None of these
A
B
What would a 10V battery do, i.e. how much charge will it provide,
when it is connected across A and B? 40 μC (20 μC) on 2 μF
HITT
A parallel-plate capacitor has a plate area of
0.2m2 and a plate separation of 0.1 mm. To
obtain an electric field of 2.0 x 106 V/m between
the plates, the magnitude of the charge on each
plate should be:
A. 8.9 x 10-7 C
B. 1.8 x 10-6 C
C.
3.5 x 10-6 C
D. 7.1 x 10-6 C
E. 1.4 x
10-5 C
More complex capacitor systems
In general a capacitor system
may consist of smaller capacitor
groups that can be identified as
connected "in parallel" or
"in series"
In the example of the figure C1 and C2 in fig.a are connected in parallel.
They can be substituted by the equivalent capacitor C12  C1  C2 as
shown in fig.b. Capacitors C12 and C3 in fig.b are connected in series.
They can be substituted by a single capacitor C123 as shown in fig.c
C123 is given by the equation:
(25 - 12)
1
1
1


C123
C12 C3
All C’s are 8.00 nF. The battery is 12 V.
What is the equivalent capacitance?
C12 = 4 nF
C123 = 12 nF
Q123 = C123 x V = 144 nC
Q3 = C3 x V = 96 nC
Q12 = C12 x V = 48 nC
U123 = ½ C123V2 = ½ x 12x10-9 x122 = 864 nJ
U1 = ½ C1V12 = ½ x 8x10-9 x62 = 144 nJ = U2
U3 = ½ x 8x10-9 x122 = 576 nF
C3 stores most energy, also the highest electric field
and most charge, the most stressed part of the circuit.
• Series combinations reduce the capacitance.
Equal C reduce by the number involved.
• In parallel the capacitance increases.
A basket of 4 capacitors, each of C = 6 nF. How
can you arrange them to get
a) 1.5 nF
b) 2 nF
g) 2.4 nF
c) 3 nF
h) 3.6 nF
d) 4 nF
i) 4.5 nF
j) 6 nF
e) 12 nF
k) 18 nF
f) 24 nF
clicker
All C’s are 8.00 nF. The battery is 12 V.
What is the equivalent capacitance?
a.
b.
c.
d.
e.
4 nF
6 nF
8 nF
10 nF
12 nF
Circuits
• All capacitors being the same, rank the
equivalent capacitances of the four circuits.
summary
C  o A/ d
 2o L / ln( b / a)
C  4o
• Capacitance
• Parallel plates, coaxial
cables, Earth
• Series and parallel
combinations
• Energy in a capacitor
• Dielectrics
• Dielectric strength
ab
 4o a
ba
b  a
Q  CV
1
1
1


 ..
C C1 C2
C  C
C  C1  C2  ...
2
1
Q
U  CV 2 
2
2C
A question
• Each of the four capacitors shown is 500 μF.
The voltmeter reads 1000V. The magnitude of
the charge, in coulombs, on each capacitor
plate is:
A. 0.2
these
B. 0.5
C. 20 D. 50 E. none of