* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download GEOG370_Ch3p2
History of geography wikipedia , lookup
Iberian cartography, 1400–1600 wikipedia , lookup
Diver navigation wikipedia , lookup
History of navigation wikipedia , lookup
Contour line wikipedia , lookup
Counter-mapping wikipedia , lookup
History of cartography wikipedia , lookup
Cartography wikipedia , lookup
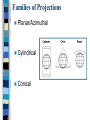
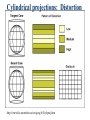
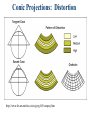
Map Basics, partII GEOG 370 Christine Erlien, Instructor Previously in Ch. 3 Symbolization Simplification/generalization Classification Scale Reference & Thematic Maps Major Map Elements Wrapping up with: Projections Grid systems Geographic Data Features must be referenced to some real world location Georeferencing Geographic Data & Position Important elements must agree: – scale – ellipsoid – datum – projection – coordinate system Geographic Data & Position: Scale When is this is an issue? – When data created for use at a particular scale are used at another Why is this an issue? – All features are stored with precise coordinates, regardless of the precision of the original source data – What does this mean? • Data from a mixture of scales can be displayed & analyzed in the same GIS project this can lead to erroneous or inaccurate conclusions Geographic Data & Position: Scale Example: – Location of same feature at different scales – (-114.875, 45.675) (-114.000, 45.000) • Zoomed out look like same point • Zoomed in look like separate points Take-home message: – Be aware of the scale at which data were collected metadata – Measurements will only be as good as least accurate data source Geodesy Study of the Earth’s – Size – Shape – Gravitational fields Geographic Data & Position: Ellipsoid The earth is not flat it must be round?! Not perfectly round: – Small irregularities on the surface such as mountains, basins, etc. – Distortion due to the Earth’s rotation – Irregularities due to variations in gravity Geographic Data & Position: Ellipsoid The earth’s shape is irregular – Slightly flattened at the poles – Equator bulges – Southern Hemisphere slightly larger than Northern Hemisphere Geographic Data & Position: Ellipsoid Ellipsoid: Hypothetical, non-spherical shape of earth – Note: Earth’s ellipsoid is only 1/300 off from sphere – Basis for datums • Datum: Reference for elevation on the earth’s surface Reference Ellipsoids Earth's surface not perfectly symmetrical, so ellipsoid fitting one geographical region may not fit another – Reason for different reference ellipsoids – Examples: • Clarke 1866: Used for N. America until recently • GRS80: Geodetic Reference System of 1980 • WGS84: Developed by US military, refined version of GRS80 Ellipsoids & Datums: Importance Differences exist between different ellipsoids & datums – Coordinates different in each can be significant distance – Elevation can be major differences at large scales Note: Be aware of the ellipsoid & datum for datasets you are working with Geographic Data & Position: Projection Projection: Process by which the round earth is portrayed on a flat map To project – Think of a light inside the globe, projecting outlines of continents onto a piece of paper wrapped around globe Process of Map Projection 1. Scale change – Actual globe reference globe based on desired scale (e.g. 1:1,000,000) 2. Reference globe mathematically projected onto flat surface Families of Projections Planar/Azimuthal Cylindrical Conical Cylindrical projections http://www.progonos.com/furuti/MapProj/Normal/ProjCyl/projCyl.html Cylindrical projections General properties: – Meridians equally spaced – Spacing between parallels of latitude increases toward poles – On globe, longitude lines converge at poles cylindrical projection forces them to be parallel – The farther away a point is from the tangent line (where cylinder contacts the globe), the greater the distortion – Useful for sailing (No direction distortion) Cylindrical projections: Distortion http://www.fes.uwaterloo.ca/crs/geog165/cylproj.htm Conic Projections Conic projections are created by setting a cone over a globe and projecting light from the center of the globe onto the cone. Conic Projections General properties: – Contact with globe along either 1 or 2 lines of latitude – Longitude lines projected onto the conical surface, meeting at its apex – Latitude lines projected onto the cone as rings – Distance between longitude lines widens as their distance from the apex increases – Typically used for mid-latitude zones with an east-to-west orientation Conic Projections From Getting Started with Geographic Information Systems, Keith C. Clarke Conic Projections: Distortion http://www.fes.uwaterloo.ca/crs/geog165/conproj.htm Azimuthal/Planar Projections Planar projections, also called azimuthal projections, project map data onto a flat surface. When the plane touches the earth at either the north or south poles latitude lines appear as concentric circles and longitude lines radiate from the pole at their true angle like the spokes on a wheel. This particular map projection's light source originates at the center of the earth but this is not true for all planar map projections. (ESRI Press) Azimuthal/Planar Projections General properties: – Tangent to the globe at one point – North & South Poles most common contact points • Longitude lines converge at the pole • Distance between longitude lines increases as the distance from the pole increases • Latitude lines appear as a series of concentric circles. – Used most often to map polar regions Azimuthal/Planar Projections:Distortion http://www.fes.uwaterloo.ca/crs/geog165/azproj.htm Map projections: Distortion Converting from 3-D globe to flat surface causes distortion Types of distortion – Shape – Area – Distance – Direction No projection can preserve all four of these spatial properties Map projections: Distortion Shape – The ability of a map projection to maintain shape of geographic features – Conformal projections: Map projections that maintain shapes/angles, scale factor locally • Best used on small areas difficult to maintain true angles for large areas • Distorts area • Application: Marine or air navigation Conformal projections Example: Mercator Map projections: Distortion Area – The ability of a map projection to maintain equal area for geographic features (e.g., correct area relative to one another) – Equal area projections: Map projections that maintain this property • Application: Instruction & small-scale general reference maps – No map projection can preserve both conformality and equal area Equal area projections Example: Mollweide Distortion minimal near the intersection of Equator & central meridian, increases toward the edges of the map Map projections: Distortion Distance – Map projection's ability to maintain true distance • Maintained for only certain parallels or meridians OR • Maintained in all directions around 1 or 2 points Equidistant projections http://www.fes.uwaterloo.ca/crs/geog165/cylproj.htm#Equidistant%20Projections Map projections: Distortion Direction – Map projection's ability to maintain true direction between geographic locations – Azimuthal map projections: Maintain direction with respect to 1 or 2 points • Angle of a line drawn between any two locations on the projection gives the correct direction with respect to true north • Application: Navigation Azimuthal projections Lambert azimuthal Tangent to North Pole http://www.warnercnr.colostate.edu/class_info/nr502/lg2/projection_descriptions /lambert_azimuthal.html