* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download g - Cloudfront.net
Heat capacity wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
Equipartition theorem wikipedia , lookup
Heat transfer wikipedia , lookup
Thermal conduction wikipedia , lookup
Heat equation wikipedia , lookup
Thermodynamic system wikipedia , lookup
Adiabatic process wikipedia , lookup
First law of thermodynamics wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
Conservation of energy wikipedia , lookup
Internal energy wikipedia , lookup
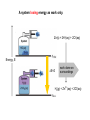
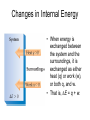
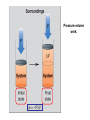
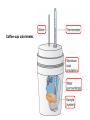
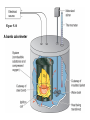
Chapter 8 Thermochemistry 8.1 Principles of Heat Flow 8.2 Calorimetry 8.3 Enthalpy 8.4 Thermochemical Equations. Hess’s Law 8.5 Enthalpies of Formation 8.6 Bond Enthalpy 8.7 The First Law of Thermodynamics Thermodynamics is the study of heat and its transformations. Thermochemistry is a branch of thermodynamics that deals with the heat involved with chemical and physical changes. Fundamental premise When energy is transferred from one object to another, it appears as work and/or as heat. For our work we must define a system to study; everything else then becomes the surroundings. The system is composed of particles with their own internal energies (E or U). Therefore the system has an internal energy. When a change occurs, the internal energy changes. A chemical system and its surroundings. the surroundings the system Energy is the capacity to do work. Potential Energy energy due to the position of an object or energy due to composition which can be released in a chemical reaction Kinetic Energy energy due to the motion of the object Potential and kinetic energy can be interconverted. Energy is the capacity to do work. Figure A less stable, Ep= mgh change in potential energy EQUALS kinetic energy more stable, Ek= 1/2 mv2 A gravitational system. The potential energy of a lifted weight is converted to kinetic energy as the weight falls. Energy is the capacity to do work. Figure B less stable change in potential energy EQUALS kinetic energy more stable A system of two balls attached by a spring. The potential energy gained by a stretched spring is converted to kinetic energy when the moving balls are released. Energy is the capacity to do work. Figure C less stable change in potential energy EQUALS kinetic energy more stable A system of oppositely charged particles. The potential energy gained when the charges are separated is converted to kinetic energy as the attraction pulls these charges together. Energy is the capacity to do work. Figure D less stable change in potential energy EQUALS kinetic energy more stable A system of fuel and exhaust. A fuel is higher in chemical potential energy than the exhaust. As the fuel burns, some of its potential energy is converted to the kinetic energy of the moving car. Energy diagrams for the transfer of internal energy (E) between a system and its surroundings. DE = Efinal - Einitial = Eproducts - Ereactants Internal Energy, E, of the system consists of potential (composition, state of subdivision), and kinetic (vibrational, rotational, and translational) energies. A system transferring energy as heat only. A system losing energy as work only. Zn(s) + 2H+(aq) + 2Cl-(aq) Energy, E DE<0 work done on surroundings H2(g) + Zn2+(aq) + 2Cl-(aq) Changes in Internal Energy • If DE < 0, Efinal < Einitial – Therefore, the system released energy to the surroundings. – This energy change is called exergonic, or exothermic. Changes in Internal Energy • When energy is exchanged between the system and the surroundings, it is exchanged as either heat (q) or work (w), or both q, and w. • That is, DE = q + w. The Sign Conventions* for q, w and DE q + w = DE + + + + - depends on sizes of q and w - + depends on sizes of q and w - - - * For q: + means system gains heat; - means system loses heat. * For w: + means word done on system; - means work done by system. DEuniverse = DEsystem + DEsurroundings Units of Energy Joule (J) 1 J = 1 kg·m2/s2 Calorie (cal) 1 cal = 4.184 J British Thermal Unit 1 Btu = 1055 J Two different paths for the energy change of a system. State Functions Usually we have no way of knowing the internal energy of a system; finding that value is simply too complex a problem. – In the system below, the water could have reached room temperature from either direction. However, we do know that the internal energy of a system is independent of the path by which the system achieved that state. State Functions • A state function depends only on the current state of a system. The change in a state function between two states is independent of the pathway between them. • Therefore, internal energy is a state function. • And so, DE depends only on Einitial and Efinal. State Functions • However, q and w are not state functions. • Whether the battery is shorted out (a) or is discharged by running the fan (b), its DE is the same. But q and w are different in the two cases! Sample Problem PROBLEM: PLAN: Determining the Change in Internal Energy of a System When gasoline burns in a car engine, the heat released causes the products CO2 and H2O to expand, which pushes the pistons outward. Excess heat is removed by the car’s cooling system. If the expanding gases do 451 J of work on the pistons and the system loses 325 J to the surroundings as heat, calculate the change in energy (DE) in J, kJ, and kcal. Define system and surroundings, assign signs to q and w and calculate DE. The answer should be converted from J to kJ and then to kcal. SOLUTION: q = - 325 J DE = q + w = -776J kJ 103J w = - 451 J -325 J + (-451 J) = -776 J = -0.776kJ -0.776kJ kcal 4.18kJ = -0.185 kcal Pressure-volume work. Sample Problem 1. A system expands against a constant pressure of 1.50 atm from 10.0 L to 25.0 L, while absorbing 150 J of heat. Determine the change in internal energy, ∆E. [1 L·atm = 101.3 J] Plan: Find work done by the system, add to heat change. w = -P∆V = -(1.50 atm)(25.0 L - 10.0 L)(101.3 J/L·atm) = - 2279.25 J = - 2280 J ∆E = q + w = 150 J - 2280 J = -2130 J Enthalpy • If a process takes place at constant pressure (as the majority of processes we study do) and the only work done is this pressure-volume work, we can account for heat flow during the process by measuring the enthalpy of the system. • Enthalpy is the internal energy plus the product of pressure and volume: H = E + PV Enthalpy • When the system changes at constant pressure, the change in enthalpy, DH, is DH = D(E + PV) • This can be written DH = DE + PDV Enthalpy • Since DE = q + w and w = - PDV, we can substitute these into the enthalpy expression: DH = DE + PDV DH = (q+w) - w DH = qp • So, at constant pressure the change in enthalpy is the heat gained or lost. The Truth about Enthalpy 1. Enthalpy is an extensive property. 2. DH for a reaction in the forward direction is equal in size, but opposite in sign, to DH for the reverse reaction. 3. DH for a reaction depends on the state of the products and the state of the reactants, that is ∆H is a state function. The Meaning of Enthalpy w = - PDV H = E + PV DH ≈ DE in 1. Reactions that do not involve gases. where H is enthalpy DH = DE + PDV qp = DE + PDV = DH 2. Reactions in which the number of moles of gas does not change. 3. Reactions in which the number of moles of gas does change but q is >>> (much, much, much greater) PDV When gases are involved, ∆H = ∆E + ∆nRT Where ∆n = moles gaseous products - moles gaseous reactants. Enthalpy diagrams for exothermic and endothermic processes. CH4(g) + 2O2(g) CO2(g) + 2H2O(g) H2O(l) CH4 + 2O2 H2O(g) DH < 0 heat out Enthalpy, H Enthalpy, H Hinitial DH > 0 CO2 + 2H2O H2O(l) Hfinal A Exothermic process B H2O(g) Hfinal heat in Hinitial Endothermic process Some Important Types of Enthalpy Change heat of combustion (DHcomb) C4H10(l) + 13/2O2(g) 4CO2(g) + 5H2O(g) heat of formation (DHf) K(s) + 1/2Br2(l) KBr(s) heat of fusion (DHfus) NaCl(s) NaCl(l) heat of vaporization (DHvap) C6H6(l) C6H6(g) Sample Problem PROBLEM: Finding the Quantity of Heat from Specific Heat Capacity A layer of copper welded to the bottom of a skillet weighs 125 g. How much heat is needed to raise the temperature of the copper layer from 250C to 300.0C? The specific heat capacity (Sp) of Cu is 0.387 J/g·˚C. PLAN: Given the mass, specific heat capacity and change in temperature, we can use q = Sp x mass x DT to find the answer. DT in 0C is the same as for K. SOLUTION: q= 0.387 J g·˚C x 125 g x (300-25)0C = 1.33x104 J Coffee-cup calorimeter. Sample Problem Determining the Heat of a Reaction PROBLEM: You place 50.0 mL of 0.500 M NaOH in a coffee-cup calorimeter at 25.000C and carefully add 25.0 mL of 0.500 M HCl, also at 25.000C. After stirring, the final temperature is 27.210C. Calculate qsoln (in J) and DHrxn (in kJ/mol). (Assume the total volume is the sum of the individual volumes and that the final solution has the same density and specfic heat capacity as water: d = 1.00 g/mL and Sp = 4.184 J/g·˚C) PLAN: We need to determine the limiting reactant from the net ionic equation. The moles of NaOH and HCl as well as the total volume can be calculated. From the volume we use density to find the mass of the water formed. At this point qsoln can be calculated using the mass, c, and DT. The heat divided by the M of water will give us the heat per mole of water formed. Sample Problem Determining the Heat of a Reaction continued SOLUTION: HCl(aq) + NaOH(aq) H+(aq) + OH-(aq) NaCl(aq) + H2O(l) H2O(l) For NaOH 0.500 M x 0.0500 L = 0.0250 mol OH- For HCl 0.500 M x 0.0250 L = 0.0125 mol H+ HCl is the limiting reactant. 0.0125 mol of H2O will form during the rxn. total volume after mixing = 0.0750 L 0.0750 L x 103 mL/L x 1.00 g/mL = 75.0 g of water q = - mass x specific heat x DT = - 75.0 g x 4.184 J/g·0C x (27.21-25.00)0C = - 693.50 J (-693.50 J/0.0125 mol H2O)(kJ/103 J) = -55.5 kJ/ mol H2O formed Figure 5.10 A bomb calorimeter Sample Problem A manufacturer claims that its new dietetic dessert has “fewer than 10 Calories per serving.” To test the claim, a chemist at the Department of Consumer Affairs places one serving in a bomb calorimeter and burns it in O2(the heat capacity of the calorimeter = 8.15 kJ/˚C). The temperature increases 4.9370C. Is the manufacturer’s claim correct? PROBLEM: PLAN: Calculating the Heat of Combustion Energy conservation; qsample + qcal = 0 => - q sample = qcalorimeter SOLUTION: qcalorimeter = heat capacity x DT = 8.151 kJ/˚C x 4.937 ˚C = 40.24 kJ 40.24 kJ kcal = 9.63 kcal or Calories 4.18 kJ The manufacturer’s claim is true. AMOUNT (mol) of compound A Summary of the relationship between amount (mol) of substance and the heat (kJ) transferred during a reaction. AMOUNT (mol) of compound B molar ratio from balanced equation HEAT (kJ) DHrxn (kJ/mol) gained or lost Sample Problem PROBLEM: Using the Heat of Reaction (DHrxn) to Find Amounts The major source of aluminum in the world is bauxite (mostly aluminum oxide). Its thermal decomposition can be represented by Al2O3(s) 2Al(s) + 3/2O2(g) DHrxn = 1676 kJ If aluminum is produced this way, how many grams of aluminum can form when 1.000x103 kJ of heat is transferred? PLAN: SOLUTION: heat(kJ) 1676kJ=2mol Al mol of Al xM g of Al 1.000x103 kJ x 2 mol Al 26.98 g Al 1676 kJ 1 mol Al = 32.20 g Al Using Hess’s Law to Calculate an Unknown DH Sample Problem PROBLEM: Two gaseous pollutants that form in auto exhaust are CO and NO. An environmental chemist is studying ways to convert them to less harmful gases through the following equation: CO(g) + NO(g) CO2(g) + 1/2N2(g) DH = ? Given the following information, calculate the unknown DH: Equation A: CO(g) + 1/2O2(g) Equation B: N2(g) + O2(g) PLAN: CO2(g) DHA = -283.0 kJ 2NO(g) DHB = 180.6 kJ Equations A and B have to be manipulated by reversal and/or multiplication by factors in order to sum to the first, or target, equation. SOLUTION: Multiply Equation B by 1/2 and reverse it. CO(g) + 1/2O2(g) NO(g) CO2(g) 1/2N2(g) + 1/2O2(g) CO(g) + NO(g) CO2(g) + 1/2N2(g) DHA = -283.0 kJ DHB = -90.3 kJ DHrxn = -373.3 kJ Sample Problem PROBLEM: Writing Formation Equations Write balanced equations for the formation of 1 mol of the following compounds from their elements in their standard states and include DH0f. (a) Silver chloride, AgCl, a solid at standard conditions. (b) Calcium carbonate, CaCO3, a solid at standard conditions. (c) Hydrogen cyanide, HCN, a gas at standard conditions. PLAN: Use the table of heats of formation for values. SOLUTION: (a) Ag(s) + 1/2Cl2(g) DH0f = -127.0 kJ AgCl(s) (b) Ca(s) + C(graphite) + 3/2O2(g) (c) 1/2H2(g) + C(graphite) + 1/2N2(g) CaCO3(s) HCN(g) DH0f = -1206.9 kJ DH0f = 135 kJ Elements -DH0f formation Reactants decomposition Enthalpy, H The general process for determining DH0rxn from DH0f values. DH0f Hinitial DH0rxn Products DH0rxn = S mDH0f(products) - S nDH0f(reactants) Hfinal Sample Problem PROBLEM: Calculating the Heat of Reaction from Heats of Formation Nitric acid, whose worldwide annual production is about 8 billion kilograms, is used to make many products, including fertilizer, dyes, and explosives. The first step in the industrial production process is the oxidation of ammonia: 4NH3(g) + 5O2(g) 4NO(g) + 6H2O(g) Calculate DH0rxn from DH0f values. PLAN: Look up the DH0f values and use Hess’s Law to find DHrxn. SOLUTION: DHrxn = S mDH0f (products) - S nDH0f (reactants) DHrxn = [4(DH0f NO(g) + 6(DH0f H2O(g)] - [4(DH0f NH3(g) + 5(DH0f O2(g)] = (4 mol)(90.3 kJ/mol) + (6 mol)(-241.8 kJ/mol) [(4 mol)(-45.9 kJ/mol) + (5 mol)(0 kJ/mol)] DHrxn = -906 kJ State Functions Usually we have no way of knowing the internal energy of a system; finding that value is simply too complex a problem.










































![Second review [Compatibility Mode]](http://s1.studyres.com/store/data/003692853_1-a578e4717b0c8365c11d7e7f576654ae-150x150.png)




