* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Intro to Probability
Survey
Document related concepts
Transcript
Intro to Probability
Objectives:
To evaluate the big idea in Probability:
chance behavior is unpredictable in the
short run but has a regular and
predictable pattern in the long run
(Law of Large Numbers).
To use Venn diagrams as a visual aid
for understanding concepts in context
Warm-up:
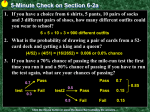
1. If you have 6 different books to place on a
bookshelf, how many different arrangements
are possible?
654321=720
2. How many different combinations exist for
your locker?
503 =125000
3. How many different locker combinations
would there be if you could only use each
number once? 504948 =117600
Questions in modern day probability:
Should I spend money on a warranty for
my new Ipod?
If I test positive for a rare blood disease,
does this mean that I definitely have this
disease?
Can we determine the chances of a child
having a psychological disorder based on
heredity?
Random Phenomenon
A phenomenon is
random if individual
outcomes are uncertain,
but there is a predictable
distribution of outcomes
over many repetitions.
Experimental versus Theoretical Probability
Probability
The probability of any outcome of a
random phenomenon is the
proportion of times the outcome
would occur in a very long series of
repetitions. (Probability is basically
long term relative frequency)
Sample Space (S)
The set of all possible outcomes for some
type of random phenomenon
Examples:
Coin Toss S = {H, T}
Fair die
S = {1, 2, 3, 4, 5, 6}
Toss a coin twice S = {HH, TT, HT, TH}
How many outcomes are there in the sample
space for rolling two dice?
36
Event
An event is any outcome or a set of outcomes of
a random phenomenon.
An event is basically a subset of the sample
space.
Examples:
Rolling a Prime #
A = {2, 3, 5}
Rolling a Prime # or an even #
B = {2, 3, 4, 5, 6}
Complement
c
E
Consists of all outcomes that are not in the
event
Example:
Rolling an even #
E={2,4,6}
Complement: Not rolling an even #
EC={1,3,5}
Union
E AB
the event A or B happening
consists of all outcomes that
are in at least one of the two
events
Ex. Rolling a prime # or even number
W ={2,3,4,5,6}
Intersection E A B
the event A and B happening
consists of all outcomes that
are in both events
Example:
Drawing a red card and a “2”
L = {2 of hearts, 2 of diamonds}
Mutually Exclusive (disjoint)
two events have no outcomes in
common
Example:
The event of rolling an even # is
disjoint from the event of rolling an
odd #
Probability model
Mathematical description of a random
phenomenon consisting of two parts
1. A sample space (S)
2. A method of assigning probabilities to
each event
We will focus on part 1 today…
Tree Diagram
It is very important to check that we have
not overlooked any possible outcome.
One visual method of checking
this is making use of a
tree diagram.
Ex. Flip a coin, then roll a die
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Multiplication Principle
If you can do one task in x number of ways and a
second task in y number of ways, then the sample
space of both task can be shown with x ● y
possible outcomes.
Example:
Tossing a coin – two possible outcomes
Rolling a die – six possible outcomes
Tossing a coin, then rolling a die:
2 ● 6 = 12 possible outcomes
Venn Diagrams
Used to display
relationships between
events
Helpful in calculating
probabilities
Venn diagram - Complement of A
AA
Venn diagram - A or B
A
B
Venn diagram - A and B
A
B
Venn diagram - disjoint events
A
B
Independence
The outcome of one trial must not influence
the outcome of another trial.
This is a major concept in statistics that is
often neglected in the design and data
collection process.
We will look at independence both logically
and mathematically in this course.
Closing:
1. In your own words, describe random phenomena.
1. Write down the symbol, key word, and visual display
for Union
1. Write down the symbol, key word, and visual display
for Intersection