Download Lecture 06. Average values

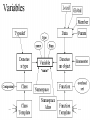
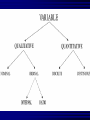
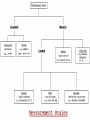
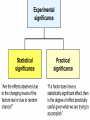
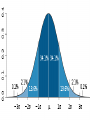
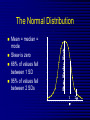
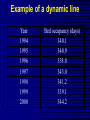
Average values
Measures of Association
Measures of Association




Absolute risk
- The relative risk and odds ratio provide a measure of risk
compared with a standard.
Attributable risk or Risk difference is a measure of absolute
risk. It represents the excess risk of disease in those exposed
taking into account the background rate of disease. The
attributable risk is defined as the difference between the
incidence rates in the exposed and non-exposed groups.
Population Attributable Risk is used to describe the excess
rate of disease in the total study population of exposed and
non-exposed individuals that is attributable to the exposure.
Number needed to treat (NNT)
- The number of patients who would need to be treated to
prevent one adverse outcome is often used to present the
results of randomized trials.
Relative Values
As a result of statistical research during
processing of the statistical data of
disease, mortality rate, lethality, etc.
absolute numbers are received, which
specify the number of the phenomena.
Though absolute numbers have a
certain cognitive values, but their use is
limited.
Relative Values
In order to acquire a level of the phenomenon,
for comparison of a parameter in dynamics or
with a parameter of other territory it is
necessary to calculate relative values
(parameters, factors) which represent result
of a ratio of statistical numbers between itself.
The basic arithmetic action at subtraction of
relative values is division.
In medical statistics themselves the
following kinds of relative parameters
are used:





Extensive;
Intensive;
Relative intensity;
Visualization;
Correlation.
The extensive parameter, or a
parameter of distribution,
characterizes a parts of the
phenomena (structure), that is it
shows, what part from the general
number of all diseases (died) is
made with this or that disease
which enters into total.
The role of Biostatisticians
Biostatisticians play essential roles in designing
studies, analyzing data and creating methods
to attack research problems as diverse as
 determination of major risk factors for heart
disease, lung disease and cancer
 testing of new drugs to combat AIDS
 evaluation of potential environmental factors
harmful to human health, such as tobacco
smoke, asbestos or pollutants
Applications of Biostatistics





Public health, including epidemiology, health services
research, nutrition, and environmental health
Design and analysis of clinical trials in medicine
Genomics, population genetics, and statistical genetics in
populations in order to link variation in genotype with a
variation in phenotype. This has been used in agriculture
to improve crops and farm animals. In biomedical
research, this work can assist in finding candidates for
gene alleles that can cause or influence predisposition to
disease in human genetics
Ecology
Biological sequence analysis
Applications of Biostatistics
Statistical methods are beginning to be
integrated into
 medical informatics
 public health informatics
 bioinformatics
Types of Data

Categorical data:  values belong to categories
- Nominal data: there is no natural order to the
categories e.g. blood groups
- Ordinal data: there is natural order e.g. Adverse
Events (Mild/Moderate/Severe/Life Threatening)
- Binary data: there are only two possible categories
e.g. alive/dead

Numerical data:  the value is a number
(either measured or counted)
- Continuous data: measurement is on a continuum
e.g. height, age, haemoglobin
- Discrete data: a “count” of events e.g. number of
pregnancies
Measures of Frequency of Events

Incidence
- The number of new events (e.g. death or a particular
disease) that occur during a specified period of time in
a population at risk for developing the events.

Incidence Rate
- A term related to incidence that reports the number of
new events that occur over the sum of time individuals
in the population were at risk for having the event (e.g.
events/person-years).

Prevalence
- The number of persons in the population affected by a
disease at a specific time divided by the number of
persons in the population at the time.
Measures of Association

Relative risk and cohort studies
- The relative risk (or risk ratio) is defined as the
ratio of the incidence of disease in the
exposed group divided by the corresponding
incidence of disease in the unexposed group.

Odds ratio and case-control studies
- The odds ratio is defined as the odds of
exposure in the group with disease divided by
the odds of exposure in the control group.
Measures of Association
Measures of Association




Absolute risk
- The relative risk and odds ratio provide a measure of risk
compared with a standard.
Attributable risk or Risk difference is a measure of absolute
risk. It represents the excess risk of disease in those exposed
taking into account the background rate of disease. The
attributable risk is defined as the difference between the
incidence rates in the exposed and non-exposed groups.
Population Attributable Risk is used to describe the excess
rate of disease in the total study population of exposed and
non-exposed individuals that is attributable to the exposure.
Number needed to treat (NNT)
- The number of patients who would need to be treated to
prevent one adverse outcome is often used to present the
results of randomized trials.
Terms Used To Describe The
Quality Of Measurements
Reliability is variability between subjects
divided by inter-subject variability plus
measurement error.
 Validity refers to the extent to which a test
or surrogate is measuring what we think it
is measuring.

Measures Of Diagnostic Test
Accuracy




Sensitivity is defined as the ability of the test to identify
correctly those who have the disease.
Specificity is defined as the ability of the test to identify
correctly those who do not have the disease.
Predictive values are important for assessing how
useful a test will be in the clinical setting at the individual
patient level. The positive predictive value is the
probability of disease in a patient with a positive test.
Conversely, the negative predictive value is the
probability that the patient does not have disease if he
has a negative test result.
Likelihood ratio indicates how much a given diagnostic
test result will raise or lower the odds of having a disease
relative to the prior probability of disease.
Measures Of Diagnostic Test
Accuracy
Expressions Used When
Making Inferences About Data

Confidence Intervals
- The results of any study sample are an estimate of the true value
in the entire population. The true value may actually be greater or
less than what is observed.



Type I error (alpha) is the probability of incorrectly
concluding there is a statistically significant difference in
the population when none exists.
Type II error (beta) is the probability of incorrectly
concluding that there is no statistically significant
difference in a population when one exists.
Power is a measure of the ability of a study to detect a
true difference.
Kaplan-Meier Survival Curves
Why Use Statistics?
Cardiovascular Mortality in Males
1,2
1
0,8
SMR 0,6
0,4
0,2
0
'35-'44 '45-'54 '55-'64 '65-'74 '75-'84
Bangor
Roseto
Percentage of Specimens Testing
Positive for RSV (respiratory syncytial virus)
Jul Aug Sep Oct Nov Dec Jan Feb Mar Apr May Jun
South 2
2
5
7
20
30
15
20
15
8
4
3
North- 2
east
West 2
3
5
3
12
28
22
28
22
20
10
9
2
3
3
5
8
25
27
25
22
15
12
2
2
3
2
4
12
12
12
10
19
15
8
Midwest
Descriptive Statistics
Percentage of Specimens Testing Postive for
RSV 1998-99
South
Northeast
West
Midwest
D
ec
Ja
n
Fe
b
M
ar
A
pr
M
ay
Ju
n
Ju
l
Ju
l
A
ug
Se
p
O
ct
N
ov
35
30
25
20
15
10
5
0
Distribution of Course Grades
14
12
10
Number of
Students
8
6
4
2
0
A
A- B+ B
B- C+ C
Grade
C- D+ D
D-
F
The Normal Distribution




Mean = median =
mode
Skew is zero
68% of values fall
between 1 SD
95% of values fall
between 2 SDs
Mean, Median, Mode
.
1

2
Hypertension Trial
DRUG Baseline mean SBP F/u mean SBP
A
150
130
B
150
125
30 Day % Mortality
Study
IC STK Control
p
N
Khaja
5.0
10.0
0.55
40
Anderson
4.2
15.4
0.19
50
Kennedy
3.7
11.2
0.02 250
95% Confidence Intervals
Khaja
(n=40)
Anderson
(n=50)
Kennedy
(n=250)
-,40 -,35 -,30 -,25 -,20 -,15 -,10 -,05 ,00
,05
,10
,15
,20
Types of Errors
Truth
No
difference
Conclusion
TYPE II
ERROR ()
No
difference
Difference
Difference
TYPE I
ERROR ()
Power = 1-
Using this parameter, it is possible to
determine the structure of patients
according to age, social status, etc. It is
accepted to express this parameter in
percentage, but it can be calculated and in
parts per thousand case when the part of
the given disease is small and at the
calculation in percentage it is expressed as
decimal fraction, instead of an integer.
The general formula of its calculation is the
following:
part × 100
total




The intensive parameter characterizes frequency
or distribution.
It shows how frequently the given phenomenon
occurs in the given environment.
For example, how frequently there is this or that
disease among the population or how frequently
people are dying from this or that disease.
To calculate the intensive parameter, it is
necessary to know the population or the
contingent.

General formula of the calculation is the
following:
phenomenon×100 (1000; 10 000; 100 000)
environment
General mortality rate
number of died during the year × 1000
number of the population


Parameters of relative intensity represent a
numerical ratio of two or several structures of
the same elements of a set, which is studied.
They allow determining a degree of conformity
(advantage or reduction) of similar attributes
and are used as auxiliary reception; in those
cases where it isn’t possible to receive direct
intensive parameters or if it is necessary to
measure a degree of a disproportion in
structure of two or several close processes.



The parameter of correlation characterizes the
relation between diverse values.
For example, the parameter of average bed
occupancy, nurses, etc.
The techniques of subtraction of the correlation
parameter is the same as for intensive
parameter, nevertheless the number of an
intensive parameter stands in the numerator, is
included into denominator, where as in a
parameter of visualization of numerator and
denominator different.


The parameter of visualization characterizes
the relation of any of comparable values to the
initial level accepted for 100. This parameter is
used for convenience of comparison, and also
in case shows a direction of process (increase,
reduction) not showing a level or the numbers
of the phenomenon.
It can be used for the characteristic of dynamics
of the phenomena, for comparison on separate
territories, in different groups of the population,
for the construction of graphic.
SIMULATION
Consider a box containing chips or cards,
each of which is numbered either 0 or 1.
We want to take a sample from this box in
order to estimate the percentage of the
cards that are numbered with a 1. The
population in this case is the box of cards,
which we will call the population box. The
percentage of cards in the box that are
numbered with a 1 is the parameter π.
SIMULATION
In the Harris study the parameter π is
unknown. Here, however, in order to see
how samples behave, we will make our
model with a known percentage of cards
numbered with a 1, say π = 60%. At the
same time we will estimate π, pretending
that we don’t know its value, by examining
25 cards in the box.
SIMULATION
We take a simple random sample with replacement
of 25 cards from the box as follows. Mix the box of
cards; choose one at random; record it; replace it;
and then repeat the procedure until we have
recorded the numbers on 25 cards. Although
survey samples are not generally drawn with
replacement, our simulation simplifies the analysis
because the box remains unchanged between
draws; so, after examining each card, the chance
of drawing a card numbered 1 on the following
draw is the same as it was for the previous draw, in
this case a 60% chance.
SIMULATION
Let’s say that after drawing the 25 cards this way,
we obtain the following results, recorded in 5
rows of 5 numbers:
SIMULATION
Based on this sample of 25 draws, we want to guess
the percentage of 1’s in the box. There are 14
cards numbered 1 in the sample. This gives us a
sample percentage of p=14/25=.56=56%. If this is
all of the information we have about the population
box, and we want to estimate the percentage of 1’s
in the box, our best guess would be 56%. Notice
that this sample value p = 56% is 4 percentage
points below the true population value π = 60%.
We say that the random sampling error (or simply
random error) is -4%.
ERROR ANALYSIS
An experiment is a procedure which
results in a measurement or
observation. The Harris poll is an
experiment which resulted in the
measurement (statistic) of 57%. An
experiment whose outcome depends
upon chance is called a random
experiment.
ERROR ANALYSIS
On repetition of such an experiment one
will typically obtain a different
measurement or observation. So, if the
Harris poll were to be repeated, the
new statistic would very likely differ
slightly from 57%. Each repetition is
called an execution or trial of the
experiment.
ERROR ANALYSIS
Suppose we made three more series of draws,
and the results were + 16%, + 0%, and +
12%. The random sampling errors of the four
simulations would then average out to:
ERROR ANALYSIS

Note that the cancellation of the positive and
negative random errors results in a small average.
Actually with more trials, the average of the
random sampling errors tends to zero.
ERROR ANALYSIS
So in order to measure a “typical size” of a random
sampling error, we have to ignore the signs. We
could just take the mean of the absolute values
(MA) of the random sampling errors. For the four
random sampling errors above, the MA turns out to
be
ERROR ANALYSIS
The MA is difficult to deal with theoretically because
the absolute value function is not differentiable at
0. So in statistics, and error analysis in general, the
root mean square (RMS) of the random sampling
errors is generally used. For the four random
sampling errors above, the RMS is
ERROR ANALYSIS
The RMS is a more conservative
measure of the typical size of the
random sampling errors in the
sense that MA ≤ RMS.
ERROR ANALYSIS
For a given experiment the RMS of all possible
random sampling errors is called the standard
error (SE). For example, whenever we use a
random sample of size n and its percentages p to
estimate the population percentage π, we have
Dynamic analysis
 Health
of people and activity of
medical establishments change in
time.
 Studying of dynamics of the
phenomena is very important for the
analysis of a state of health and
activity of system of public health
services.
Example of a dynamic line
Year
1994
1995
1996
1997
1998
1999
2000
Bed occupancy (days)
340.1
340.9
338.0
343.0
341.2
339.1
344.2
Parameters applied for analysis
of changes of a phenomenon
of growth –relation of all
numbers of dynamic lines to
the previous level accepted for
100 %.
 Rate
Parameters applied for
analysis of changes of a
phenomenon
gain – difference
between next and previous
numbers of dynamic lines.
 Pure
Parameters applied for
analysis of changes of a
phenomenon
of gain – relation of the
pure gain to previous
number.
 Rate
Parameters applied for
analysis of changes of a
phenomenon
of visualization —
relation of all numbers of
dynamic lines to the first level,
which one starts to 100%.
 Parameter
Measures of Association
Measures of Association




Absolute risk
- The relative risk and odds ratio provide a measure of risk
compared with a standard.
Attributable risk or Risk difference is a measure of absolute
risk. It represents the excess risk of disease in those exposed
taking into account the background rate of disease. The
attributable risk is defined as the difference between the
incidence rates in the exposed and non-exposed groups.
Population Attributable Risk is used to describe the excess
rate of disease in the total study population of exposed and
non-exposed individuals that is attributable to the exposure.
Number needed to treat (NNT)
- The number of patients who would need to be treated to
prevent one adverse outcome is often used to present the
results of randomized trials.
Relative Values
As a result of statistical research during
processing of the statistical data of
disease, mortality rate, lethality, etc.
absolute numbers are received, which
specify the number of the phenomena.
Though absolute numbers have a
certain cognitive values, but their use is
limited.
Relative Values
In order to acquire a level of the phenomenon,
for comparison of a parameter in dynamics or
with a parameter of other territory it is
necessary to calculate relative values
(parameters, factors) which represent result
of a ratio of statistical numbers between itself.
The basic arithmetic action at subtraction of
relative values is division.
In medical statistics themselves the
following kinds of relative parameters
are used:





Extensive;
Intensive;
Relative intensity;
Visualization;
Correlation.
The extensive parameter, or a
parameter of distribution,
characterizes a parts of the
phenomena (structure), that is it
shows, what part from the general
number of all diseases (died) is
made with this or that disease
which enters into total.
Using this parameter, it is possible to
determine the structure of patients
according to age, social status, etc. It is
accepted to express this parameter in
percentage, but it can be calculated and in
parts per thousand case when the part of
the given disease is small and at the
calculation in percentage it is expressed as
decimal fraction, instead of an integer.
The general formula of its calculation is the
following:
part × 100
total




The intensive parameter characterizes frequency
or distribution.
It shows how frequently the given phenomenon
occurs in the given environment.
For example, how frequently there is this or that
disease among the population or how frequently
people are dying from this or that disease.
To calculate the intensive parameter, it is
necessary to know the population or the
contingent.

General formula of the calculation is the
following:
phenomenon×100 (1000; 10 000; 100 000)
environment
General mortality rate
number of died during the year × 1000
number of the population
SIMULATION
Let’s say that after drawing the 25 cards this way,
we obtain the following results, recorded in 5
rows of 5 numbers: