* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 06. Average values
Survey
Document related concepts
Transcript
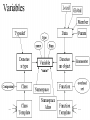
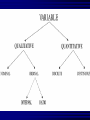
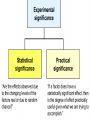
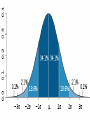
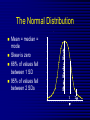
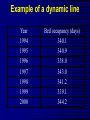
Average values Measures of Association Measures of Association Absolute risk - The relative risk and odds ratio provide a measure of risk compared with a standard. Attributable risk or Risk difference is a measure of absolute risk. It represents the excess risk of disease in those exposed taking into account the background rate of disease. The attributable risk is defined as the difference between the incidence rates in the exposed and non-exposed groups. Population Attributable Risk is used to describe the excess rate of disease in the total study population of exposed and non-exposed individuals that is attributable to the exposure. Number needed to treat (NNT) - The number of patients who would need to be treated to prevent one adverse outcome is often used to present the results of randomized trials. Relative Values As a result of statistical research during processing of the statistical data of disease, mortality rate, lethality, etc. absolute numbers are received, which specify the number of the phenomena. Though absolute numbers have a certain cognitive values, but their use is limited. Relative Values In order to acquire a level of the phenomenon, for comparison of a parameter in dynamics or with a parameter of other territory it is necessary to calculate relative values (parameters, factors) which represent result of a ratio of statistical numbers between itself. The basic arithmetic action at subtraction of relative values is division. In medical statistics themselves the following kinds of relative parameters are used: Extensive; Intensive; Relative intensity; Visualization; Correlation. The extensive parameter, or a parameter of distribution, characterizes a parts of the phenomena (structure), that is it shows, what part from the general number of all diseases (died) is made with this or that disease which enters into total. The role of Biostatisticians Biostatisticians play essential roles in designing studies, analyzing data and creating methods to attack research problems as diverse as determination of major risk factors for heart disease, lung disease and cancer testing of new drugs to combat AIDS evaluation of potential environmental factors harmful to human health, such as tobacco smoke, asbestos or pollutants Applications of Biostatistics Public health, including epidemiology, health services research, nutrition, and environmental health Design and analysis of clinical trials in medicine Genomics, population genetics, and statistical genetics in populations in order to link variation in genotype with a variation in phenotype. This has been used in agriculture to improve crops and farm animals. In biomedical research, this work can assist in finding candidates for gene alleles that can cause or influence predisposition to disease in human genetics Ecology Biological sequence analysis Applications of Biostatistics Statistical methods are beginning to be integrated into medical informatics public health informatics bioinformatics Types of Data Categorical data: values belong to categories - Nominal data: there is no natural order to the categories e.g. blood groups - Ordinal data: there is natural order e.g. Adverse Events (Mild/Moderate/Severe/Life Threatening) - Binary data: there are only two possible categories e.g. alive/dead Numerical data: the value is a number (either measured or counted) - Continuous data: measurement is on a continuum e.g. height, age, haemoglobin - Discrete data: a “count” of events e.g. number of pregnancies Measures of Frequency of Events Incidence - The number of new events (e.g. death or a particular disease) that occur during a specified period of time in a population at risk for developing the events. Incidence Rate - A term related to incidence that reports the number of new events that occur over the sum of time individuals in the population were at risk for having the event (e.g. events/person-years). Prevalence - The number of persons in the population affected by a disease at a specific time divided by the number of persons in the population at the time. Measures of Association Relative risk and cohort studies - The relative risk (or risk ratio) is defined as the ratio of the incidence of disease in the exposed group divided by the corresponding incidence of disease in the unexposed group. Odds ratio and case-control studies - The odds ratio is defined as the odds of exposure in the group with disease divided by the odds of exposure in the control group. Measures of Association Measures of Association Absolute risk - The relative risk and odds ratio provide a measure of risk compared with a standard. Attributable risk or Risk difference is a measure of absolute risk. It represents the excess risk of disease in those exposed taking into account the background rate of disease. The attributable risk is defined as the difference between the incidence rates in the exposed and non-exposed groups. Population Attributable Risk is used to describe the excess rate of disease in the total study population of exposed and non-exposed individuals that is attributable to the exposure. Number needed to treat (NNT) - The number of patients who would need to be treated to prevent one adverse outcome is often used to present the results of randomized trials. Terms Used To Describe The Quality Of Measurements Reliability is variability between subjects divided by inter-subject variability plus measurement error. Validity refers to the extent to which a test or surrogate is measuring what we think it is measuring. Measures Of Diagnostic Test Accuracy Sensitivity is defined as the ability of the test to identify correctly those who have the disease. Specificity is defined as the ability of the test to identify correctly those who do not have the disease. Predictive values are important for assessing how useful a test will be in the clinical setting at the individual patient level. The positive predictive value is the probability of disease in a patient with a positive test. Conversely, the negative predictive value is the probability that the patient does not have disease if he has a negative test result. Likelihood ratio indicates how much a given diagnostic test result will raise or lower the odds of having a disease relative to the prior probability of disease. Measures Of Diagnostic Test Accuracy Expressions Used When Making Inferences About Data Confidence Intervals - The results of any study sample are an estimate of the true value in the entire population. The true value may actually be greater or less than what is observed. Type I error (alpha) is the probability of incorrectly concluding there is a statistically significant difference in the population when none exists. Type II error (beta) is the probability of incorrectly concluding that there is no statistically significant difference in a population when one exists. Power is a measure of the ability of a study to detect a true difference. Kaplan-Meier Survival Curves Why Use Statistics? Cardiovascular Mortality in Males 1,2 1 0,8 SMR 0,6 0,4 0,2 0 '35-'44 '45-'54 '55-'64 '65-'74 '75-'84 Bangor Roseto Percentage of Specimens Testing Positive for RSV (respiratory syncytial virus) Jul Aug Sep Oct Nov Dec Jan Feb Mar Apr May Jun South 2 2 5 7 20 30 15 20 15 8 4 3 North- 2 east West 2 3 5 3 12 28 22 28 22 20 10 9 2 3 3 5 8 25 27 25 22 15 12 2 2 3 2 4 12 12 12 10 19 15 8 Midwest Descriptive Statistics Percentage of Specimens Testing Postive for RSV 1998-99 South Northeast West Midwest D ec Ja n Fe b M ar A pr M ay Ju n Ju l Ju l A ug Se p O ct N ov 35 30 25 20 15 10 5 0 Distribution of Course Grades 14 12 10 Number of Students 8 6 4 2 0 A A- B+ B B- C+ C Grade C- D+ D D- F The Normal Distribution Mean = median = mode Skew is zero 68% of values fall between 1 SD 95% of values fall between 2 SDs Mean, Median, Mode . 1 2 Hypertension Trial DRUG Baseline mean SBP F/u mean SBP A 150 130 B 150 125 30 Day % Mortality Study IC STK Control p N Khaja 5.0 10.0 0.55 40 Anderson 4.2 15.4 0.19 50 Kennedy 3.7 11.2 0.02 250 95% Confidence Intervals Khaja (n=40) Anderson (n=50) Kennedy (n=250) -,40 -,35 -,30 -,25 -,20 -,15 -,10 -,05 ,00 ,05 ,10 ,15 ,20 Types of Errors Truth No difference Conclusion TYPE II ERROR () No difference Difference Difference TYPE I ERROR () Power = 1- Using this parameter, it is possible to determine the structure of patients according to age, social status, etc. It is accepted to express this parameter in percentage, but it can be calculated and in parts per thousand case when the part of the given disease is small and at the calculation in percentage it is expressed as decimal fraction, instead of an integer. The general formula of its calculation is the following: part × 100 total The intensive parameter characterizes frequency or distribution. It shows how frequently the given phenomenon occurs in the given environment. For example, how frequently there is this or that disease among the population or how frequently people are dying from this or that disease. To calculate the intensive parameter, it is necessary to know the population or the contingent. General formula of the calculation is the following: phenomenon×100 (1000; 10 000; 100 000) environment General mortality rate number of died during the year × 1000 number of the population Parameters of relative intensity represent a numerical ratio of two or several structures of the same elements of a set, which is studied. They allow determining a degree of conformity (advantage or reduction) of similar attributes and are used as auxiliary reception; in those cases where it isn’t possible to receive direct intensive parameters or if it is necessary to measure a degree of a disproportion in structure of two or several close processes. The parameter of correlation characterizes the relation between diverse values. For example, the parameter of average bed occupancy, nurses, etc. The techniques of subtraction of the correlation parameter is the same as for intensive parameter, nevertheless the number of an intensive parameter stands in the numerator, is included into denominator, where as in a parameter of visualization of numerator and denominator different. The parameter of visualization characterizes the relation of any of comparable values to the initial level accepted for 100. This parameter is used for convenience of comparison, and also in case shows a direction of process (increase, reduction) not showing a level or the numbers of the phenomenon. It can be used for the characteristic of dynamics of the phenomena, for comparison on separate territories, in different groups of the population, for the construction of graphic. SIMULATION Consider a box containing chips or cards, each of which is numbered either 0 or 1. We want to take a sample from this box in order to estimate the percentage of the cards that are numbered with a 1. The population in this case is the box of cards, which we will call the population box. The percentage of cards in the box that are numbered with a 1 is the parameter π. SIMULATION In the Harris study the parameter π is unknown. Here, however, in order to see how samples behave, we will make our model with a known percentage of cards numbered with a 1, say π = 60%. At the same time we will estimate π, pretending that we don’t know its value, by examining 25 cards in the box. SIMULATION We take a simple random sample with replacement of 25 cards from the box as follows. Mix the box of cards; choose one at random; record it; replace it; and then repeat the procedure until we have recorded the numbers on 25 cards. Although survey samples are not generally drawn with replacement, our simulation simplifies the analysis because the box remains unchanged between draws; so, after examining each card, the chance of drawing a card numbered 1 on the following draw is the same as it was for the previous draw, in this case a 60% chance. SIMULATION Let’s say that after drawing the 25 cards this way, we obtain the following results, recorded in 5 rows of 5 numbers: SIMULATION Based on this sample of 25 draws, we want to guess the percentage of 1’s in the box. There are 14 cards numbered 1 in the sample. This gives us a sample percentage of p=14/25=.56=56%. If this is all of the information we have about the population box, and we want to estimate the percentage of 1’s in the box, our best guess would be 56%. Notice that this sample value p = 56% is 4 percentage points below the true population value π = 60%. We say that the random sampling error (or simply random error) is -4%. ERROR ANALYSIS An experiment is a procedure which results in a measurement or observation. The Harris poll is an experiment which resulted in the measurement (statistic) of 57%. An experiment whose outcome depends upon chance is called a random experiment. ERROR ANALYSIS On repetition of such an experiment one will typically obtain a different measurement or observation. So, if the Harris poll were to be repeated, the new statistic would very likely differ slightly from 57%. Each repetition is called an execution or trial of the experiment. ERROR ANALYSIS Suppose we made three more series of draws, and the results were + 16%, + 0%, and + 12%. The random sampling errors of the four simulations would then average out to: ERROR ANALYSIS Note that the cancellation of the positive and negative random errors results in a small average. Actually with more trials, the average of the random sampling errors tends to zero. ERROR ANALYSIS So in order to measure a “typical size” of a random sampling error, we have to ignore the signs. We could just take the mean of the absolute values (MA) of the random sampling errors. For the four random sampling errors above, the MA turns out to be ERROR ANALYSIS The MA is difficult to deal with theoretically because the absolute value function is not differentiable at 0. So in statistics, and error analysis in general, the root mean square (RMS) of the random sampling errors is generally used. For the four random sampling errors above, the RMS is ERROR ANALYSIS The RMS is a more conservative measure of the typical size of the random sampling errors in the sense that MA ≤ RMS. ERROR ANALYSIS For a given experiment the RMS of all possible random sampling errors is called the standard error (SE). For example, whenever we use a random sample of size n and its percentages p to estimate the population percentage π, we have Dynamic analysis Health of people and activity of medical establishments change in time. Studying of dynamics of the phenomena is very important for the analysis of a state of health and activity of system of public health services. Example of a dynamic line Year 1994 1995 1996 1997 1998 1999 2000 Bed occupancy (days) 340.1 340.9 338.0 343.0 341.2 339.1 344.2 Parameters applied for analysis of changes of a phenomenon of growth –relation of all numbers of dynamic lines to the previous level accepted for 100 %. Rate Parameters applied for analysis of changes of a phenomenon gain – difference between next and previous numbers of dynamic lines. Pure Parameters applied for analysis of changes of a phenomenon of gain – relation of the pure gain to previous number. Rate Parameters applied for analysis of changes of a phenomenon of visualization — relation of all numbers of dynamic lines to the first level, which one starts to 100%. Parameter Measures of Association Measures of Association Absolute risk - The relative risk and odds ratio provide a measure of risk compared with a standard. Attributable risk or Risk difference is a measure of absolute risk. It represents the excess risk of disease in those exposed taking into account the background rate of disease. The attributable risk is defined as the difference between the incidence rates in the exposed and non-exposed groups. Population Attributable Risk is used to describe the excess rate of disease in the total study population of exposed and non-exposed individuals that is attributable to the exposure. Number needed to treat (NNT) - The number of patients who would need to be treated to prevent one adverse outcome is often used to present the results of randomized trials. Relative Values As a result of statistical research during processing of the statistical data of disease, mortality rate, lethality, etc. absolute numbers are received, which specify the number of the phenomena. Though absolute numbers have a certain cognitive values, but their use is limited. Relative Values In order to acquire a level of the phenomenon, for comparison of a parameter in dynamics or with a parameter of other territory it is necessary to calculate relative values (parameters, factors) which represent result of a ratio of statistical numbers between itself. The basic arithmetic action at subtraction of relative values is division. In medical statistics themselves the following kinds of relative parameters are used: Extensive; Intensive; Relative intensity; Visualization; Correlation. The extensive parameter, or a parameter of distribution, characterizes a parts of the phenomena (structure), that is it shows, what part from the general number of all diseases (died) is made with this or that disease which enters into total. Using this parameter, it is possible to determine the structure of patients according to age, social status, etc. It is accepted to express this parameter in percentage, but it can be calculated and in parts per thousand case when the part of the given disease is small and at the calculation in percentage it is expressed as decimal fraction, instead of an integer. The general formula of its calculation is the following: part × 100 total The intensive parameter characterizes frequency or distribution. It shows how frequently the given phenomenon occurs in the given environment. For example, how frequently there is this or that disease among the population or how frequently people are dying from this or that disease. To calculate the intensive parameter, it is necessary to know the population or the contingent. General formula of the calculation is the following: phenomenon×100 (1000; 10 000; 100 000) environment General mortality rate number of died during the year × 1000 number of the population SIMULATION Let’s say that after drawing the 25 cards this way, we obtain the following results, recorded in 5 rows of 5 numbers: