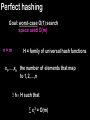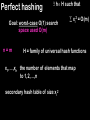Download Hashing

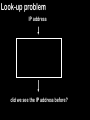
Look-up problem
IP address
did we see the IP address before?
Hashing + chaining
use IP address
as an index
IP address
hash function
linked list
index
How to choose a hash function?
depends on the distribution of the data
x [0,1]
x  x.n
interpret x as a number
x  x mod n
IP-addresses
n=256
bad
n=257
good?
Universal hash functions
choose a hash function “randomly”
n = number of entries in the hash table
U = the universe
h: U  {0,...,n-1} a hash function
Universal hash functions
choose a hash function “randomly”
n = number of entries in the hash table
U = the universe
h: U  {0,...,n-1} a hash function
a set of hash functions H is universal
if x,y U and random h  H
P ( h(x) = h(y) )  1/n
Universal hash functions
a set of hash functions H is universal
if x,y U and random h  H
P ( h(x) = h(y) )  1/n
For IP addresses
choose a1,a2,a3,a4  {0,1,...,256}
(x1,x2,x3,x4)  a1x1+a2x2+a3x3+a4x4 mod 257
Perfect hashing
Goal: worst-case O(1) search
space used O(m)
static set of elements
Perfect hashing
Goal: worst-case O(1) search
space used O(m)
static set of elements
n = m2
i.e., space used (m2)
H = family of universal hash functions
 hash function h H with no collision
Perfect hashing
Goal: worst-case O(1) search
space used O(m)
n=m
H = family of universal hash functions
x1,...,xn the number of elements that map
to 1,2,...,n
 h H such that
 xi2 = O(m)
Perfect hashing
 h H such that
Goal: worst-case O(1) search
space used O(m)
n=m
 xi2 = O(m)
H = family of universal hash functions
x1,...,xn the number of elements that map
to 1,2,...,n
secondary hash table of size xi2
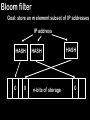
Bloom filter
Goal: store an m element subset of IP addresses
IP address
HASH
0
0
HASH
n-bits of storage
HASH
0
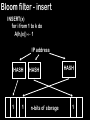
Bloom filter - insert
INSERT(x)
for i from 1 to k do
A(hi(x))  1
IP address
HASH
1
1
HASH
n-bits of storage
HASH
1
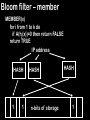
Bloom filter – member
MEMBER(x)
for i from 1 to k do
if A(hi(x))=0 then return FALSE
return TRUE
IP address
HASH
1
1
HASH
n-bits of storage
HASH
1
Bloom filter – member
MEMBER(x)
for i from 1 to k do
if A(hi(x))=0 then return FALSE
return TRUE
sometimes gives false positive answer
error parameter: false positive probability
Bloom filter – analysis
error parameter: false positive probability
m = number of items to be stored
n = number of bits of storage
k = number of hash functions
Bloom filter – analysis
error parameter: false positive probability
m = number of items to be stored
n = number of bits of storage
k = number of hash functions
p = fraction of the bits filled
p
-km/n
e
Bloom filter – analysis
error parameter: false positive probability
m = number of items to be stored
n = number of bits of storage
k = number of hash functions
p = fraction of the bits filled
false positive probability
k
(1-p)
p  e-km/n
Bloom filter – analysis
error parameter: false positive probability
m = number of items to be stored
n = number of bits of storage
k = number of hash functions
optimal
k  0.7 m/n
false positive rate  0.6185m/n