Download CHAPTER 5 PROBABILITY

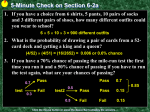
CHAPTER 5
PROBABILITY
CARDS & DICE
BLACK
RED
CLUB
SPADE
DIAMOND HEART
TOTAL
ACE
1
1
1
1
4
FACE CARD
(K, Q, J)
3
3
3
3
12
NUMBERED
CARD (1-9)
9
9
9
9
36
TOTAL
13
13
13
13
52
CARDS & DICE


Single Die: Six sides Numbered 1 to 6
Double Dice: Use the sum of the two top
sides (totals are 2 to 12)
PROBABILITY DEFINITIONS:





Probability – The likelihood that a given event
will occur. Expressed as a proportion.
Experiment – A procedure that can be
repeated that has uncertain random results.
Sample Space – All possible outcomes of an
experiment or observation – Examples.
Event – Subset of the Sample Space (could
be simple or complex).
Notation – P(A) = Probability of A occurring.
TWO WAYS TO DETERMINE:



Empirical – Trial;
Run a number of
times and count
successes; Then
#_ OF _ SUCCESSES
P( A) 
#_ OF _ TRIALS
Classical –
Calculated based on
known outcomes
P( A) 
Examples of each.
#_ OF _ WAYS _ A _ CAN _ OCCUR
#_ OF _ ALL _ POSSIBLE _ OUTCOMES
LAW OF LARGE NUMBERS

As the number of trials increases using
the Empirical Method, the closer the
trial P(A) approaches the Classical
(actual) P(A).
PROBABILITY PROPERTIES




The probability of an impossible event is 0.0.
The probability of an absolutely certain event
is 1.0.
For any event A, 0.0 ≤P(A) ≤ 1.0.
The sum of probabilities of all events in the
Sample Space is 1.0.
PROBABILITY DEFINITIONS:


Probability Model: A table listing each
outcome of the Sample Space and its
Probability of Occurrence.
For the Table to be a true Probability
model, all outcomes must be listed; all
the probabilities must meet probability
definition; and the sum of all
probabilites must add to 1.0.
PROBABILITY DEFINITIONS:

Unusual Event: Any event whose
probability is less than 0.05 or 5%.
PROBABILITY EXAMPLES
For each, show sample space as well as
probabilities:

Coins

Jar of Colored Marbles

Triplets

Cards

Dice – Do full Probability Space
DEFINE DISJOINT (5.2):

Disjoint (Mutually Exclusive) Events –
Events that can not occur simultaneous.
P  A B  0

Venn Diagram

Examples of Mutually Exclusive Events



Flipping a coin.
Drawing a card.
Picking a marble from a jar.
ADDITION (OR) RULE:

If Events A & B are Mutually Exclusive (or
disjoint), the Probability of Event A or Event
B occurring is P(A) + P(B).
P  A B   P( A)  P(B)
P  A B  0
DEFINE NOT DISJOINT (Not
Mutually Exclusive):

Examples of events that are Not
Disjoint:

Cards of number and suit.

Marbles of colors and letters.

Venn Diagram
P  A B  0
ADDITION (OR) RULE:

If Events A & B are NOT Mutually Exclusive (or
disjoint), the Probability of Event A or Event B
occurring is P(A) + P(B) – the overlap P(A and B).
P  A B   P( A)  P( B)  P  A B 
P  A B  0

AND

Venn Diagram

Use with given probabilities.
ADDITION (OR) RULE:

Examples of disjoint probabilities

Cards

Marbles

Tables
ADDITION (OR ) RULE:
FRESHMEN
SOPHOMORE
JUNIOR
SENIOR
TOTAL
SATISFIED
57
49
64
61
231
NEUTRAL
23
15
16
11
65
NOT SATISFIED
21
18
14
26
79
TOTAL
101
82
94
98
375
COMPLIMENT RULE:

 
Probability of A not occurring is P A
 
P  A  P A  1
then
 
P A  1  P  A
COMPLIMENT RULE:

If A, B, C, D & E are all possible events, then
P  A  P  B   P(C)  P  D   P  F   1
And P  A  P  B   P(C)  P  D   1  P  F 
DEFINE INDEPENDENCE(5.3):



Two events are independent if the occurrence
of one event does not affect the probability of
the occurrence of the other event.
In other words, P(B) is the same whether or
not event A has occurred or not.
Occurrence of event A does not affect
probability of event B.
MULTIPLICATION (AND) RULE:

If two events are independent then
P  A B   P  A * P  B 

Examples:

Die

Marbles with replacement.

Games
CONDITIONAL
PROBABILITY(5.4):
Means the probability of B occurring
GIVEN THAT event A has already
occurred.
P  B | A
The statement “Given That” CHANGES
THE SAMPLE SPACE.
FORMULA:
P( A  B)
P( A | B) 
P( A)
Do with given probabilities.
CONDITIONAL PROBABILITY:
FRESHMEN
SOPHOMORE
JUNIOR
SENIOR
TOTAL
SATISFIED
57
49
64
61
231
NEUTRAL
23
15
16
11
65
NOT SATISFIED
21
18
14
26
79
TOTAL
101
82
94
98
375
MULTIPLICATION RULE FOR
EVENTS THAT ARE NOT
INDEPENDENT:

If events A & B are NOT independent
P  A B   P  A * P  B | A 

Examples

Marbles without replacement

Cards without replacement

Table
MULTIPLICATION RULE FOR
LARGE POPULATION:


If the population is very large (size of a
large town) then we can consider two
events as independent even without
replacement (consider it as with
replacement).
Example of survey.
ACCEPTANCE SAMPLING
EXAMPLE:





Lot of 100 circuits has 5 defective.
Take 2 circuits without replacement. If only
one defective then reject the lot.
What is the probability of rejecting the lot?
Build tree of good/bad using conditional
probability.
Use the addition & multiplication rules to find
probability of lot being rejected.
ACCEPTANCE SAMPLING
EXAMPLE:
95/100
Pass
1st Sample
5/100
Fail
Pass 94/99
2nd Sample
Fail 5/99
Pass 95/99
2nd Sample
Fail 4/99
PROBABILITY SUMMARY


Good Summary of Probability Rules on
Page 284 of text.
There is NO relationship between
Mutually Exclusive and Independence
concepts.
COUNTING METHODS:


Using the classical method of
calculating probabilities, we need to
find better ways to count possibilities.
Example of births of triplets.
COUNTING METHODS:

Multiplication Rule with Replacement:




How many three or five digit numbers?
How many “word” combinations with 6 letters?
How many meals?
Formula: n items to select from and want to
select r items r
n
COUNTING METHODS:


Multiplication Rule without
Replacement:
Define Factorial.



How many three digit numbers using only
numbers 0, 1, 2 without replacement?
How many word combinations with 6
letters without replacement?
How many ways to arrange 5 books
without replacement?
COUNTING METHODS:



Multiplication Rule without Replacement and
with more items than options:
Have n items but only r places for them.
Order matters: PERMUTATION



8 books but only 5 places
10 people 5 offices
Formula:
n!
n pr 
 n  r !
COUNTING METHODS:



Multiplication Rule without Replacement and
with more items than options:
Have n items but only r places for them.
Order does not matter: COMBINATION




8 books but only 5 places
10 people committee of 5
Lottery
n!
Formula: n Cr 
r ! n  r !
COUNTING METHODS:
CALCULATOR FUNCTIONS
COUNTING METHODS:


Arrange n items n ways, if not all n items
are distinct.
n!
Formula:
n1 * n2 * n3 *....* nk

Where the

Example using fruits or names.
ni ' s
are non distinct items.
COUNTING METHODS:
SUMMARY ON PAGE 304
READ SECTION 5.6
PROBABILITY QUOTES



“The 50-50-90 rule: Anytime you have a 50-50
chance of getting something right, there's a 90%
probability you'll get it wrong.” Andy Rooney
“From principles is derived probability, but truth or
certainty is obtained only from facts.” Tom Stoppard
“Life is a school of probability.” Walter Bagehot
PROBABILITY