* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download texture
History of randomness wikipedia , lookup
Birthday problem wikipedia , lookup
Mixture model wikipedia , lookup
Infinite monkey theorem wikipedia , lookup
Ars Conjectandi wikipedia , lookup
Inductive probability wikipedia , lookup
Probability interpretations wikipedia , lookup
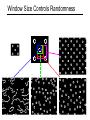
Today: Stochastic Processes Two Topics • CONDENSATION • Modeling texture Monday (3/5) • Reflectance • Environment Matting Final Project Presentations • Tentatively: Monday March 12, 2:30-4:30 Tracking We’ve seen what tracking can do Where does it fail? • occlusions • fast motions • ambiguity Need to be able to recover from failures • multiple hypothesis tracking Modeling Texture What is texture? • An image obeying some statistical properties • Similar structures repeated over and over again • Often has some degree of randomness What Do These Have in Common Tracking and texture can both be modeled by stochastic processes Stochastic Process Terminology Random variable • • • • nondeterministic value with a given probability distribution e.g. result of roll of dice discrete: can take on a finite number of possible values continuous: not discrete Probability density function (PDF) • non-negative real valued function p(x) such that • called probability distribution when x is discrete • sometimes probability distribution is used to refer to densities Discrete stochastic process • sequence or array of random variables, statistically interrelated • e.g. states of atoms in a crystal lattice Conditional probability • P[A|B,C] means probability of A given B and C • e.g. probability of snow today given snow yesterday and the day before Statistical Inference Estimation • Given measurements z = (z1, z2, ..., zn) • Compute model parameters x = (x1, x2, ..., xm) Statistical estimation • Given measurements z and uncertainty information • Compute p(x | z) – probability of every possible model Key Tool: Bayes Law likelihood (what measurement would we expect to see if we knew the model?) prior posterior (our knowledge about these parameters) (what’s the model?) normalization MAP Estimation Often we just want to maximize p(x|z) • Can ignore p(z), since it’s a constant (doesn’t depend on x) • Maximum a posteriori (MAP) estimate of x is What if no prior information? • p(x) is constant for all x (a uniform distribution) • Posterior likelihood term • Maximum likelihood estimate of x is Markov Process 1D stochastic process • a sequence of interdependent random variables xt, xt-1, xt-2, ..., x1 • xt is the state of the model at time t Markov assumption • model state depends depends only on a fixed (finite) number of previous states • First order Markov Chain • N th order Markov Chain Putting It To Work Text Synthesis • Create plausible looking poetry, love letters, term papers, congressional reports, etc. • Learn – find all blocks of N consecutive words/letters in training documents – build probabilities of these N-tuples from histogram » probability of N-tuple X = (# of occurances of X / total # N-tuples) – Create K th word by taking a random sample from » possible methods » » » » invert cumulative probability distribution (must be invertable to work) rejection sampling use importance sampling (e.g., Metropolis Algorithm) simpler: just remember the most likely N tuples beginning with previous N-1 words [Scientific American, June 1989, Dewdney] “I Spent an Interesting Evening Recently with a Grain of Salt” - Mark V. Shaney (computer-generated contributor to UseNet News group called net.singles) Output of 2nd order word-level Markov Chain after training on 90,000 word philosophical essay: “If we were to revive the fable is useless. Perhaps only the allegory of simulation is unendurable--more cruel than Artaud's Theatre of Cruelty, which was the first to practice deterrence, abstraction, disconnection, deterritorialisation, etc.; and if it were our own past. We are witnessing the end of the negative form. But nothing separates one pole from the very swing of voting ''rights'' to electoral...” Probabilistic Tracking Treat tracking problem as a Markov process • Estimate p(xt | zt, xt-1) • Combine Markov assumption with Bayes Rule measurement likelihood prediction (likelihood of seeing this measurement) (based on previous frame and motion model) Approach • Predict position at time t: • Measure (perform correlation search or Lukas-Kanade) and compute likelihood • Combine to obtain (unnormalized) state probability Kalman Filtering: assume p(x) is a Gaussian initial state prediction measurement posterior prediction Key • s = x (position) • o = z (sensor) [Schiele et al. 94], [Weiß et al. 94], [Borenstein 96], [Gutmann et al. 96, 98], [Arras 98] Robot figures courtesy of Dieter Fox Modeling Probabilities with Samples Allocate samples according to probability • Higher probability—more samples CONDENSATION [Isard & Blake] Initialization: unknown position (uniform) Measurement posterior CONDENSATION [Isard & Blake] Prediction: • draw new samples from the PDF • use the motion model to move the samples CONDENSATION [Isard & Blake] Measurement posterior Monte Carlo Robot Localization Particle Filters [Fox, Dellaert, Thrun and collaborators] CONDENSATION Contour Tracking Training a tracker CONDENSATION Contour Tracking Red: smooth drawing Green: scribble Blue: pause Modeling Texture What is texture? • An image obeying some statistical properties • Similar structures repeated over and over again • Often has some degree of randomness 2D Stochastic Process Terminology Random field • multi-dimensional stochastic process – e.g., each pixel a random variable. • a random field is stationary if statistical relationships are space-invariant (translate across the image) Markov random field • random field where each variable is conditioned on a finite neighborhood MRF’s and Images A Markov random field (MRF) • generalization of Markov chains to two dimensions. Homogeneous (stationary) first-order MRF: • probability that pixel X takes a certain value given the values of neighbors A, B, C, and D: A • P[X|A,B,C,D] D X B C • Higher order MRF’s have larger neighborhoods * * * * * X * * * * * * * * * X * * * * * * Modeling MRF’s Given training image(s) • compute p(X), p(X | A, B, C, D) based on training set – by creating histograms of pixels, neighborhoods Not quite what we want • We’d like a joint probability function over the entire image: – p(X11, X12, X13, ...) – If we had this, we could just sample random images from it • Turns out this function is a Gibbs distribution – [Geman & Geman, 1984] • However, still hard to sample from – poor convergence – can be very slow—hours, days... Texture Synthesis [Efros & Leung, ICCV 99] Simpler algorithm, avoids Gibbs sampling Synthesizing One Pixel SAMPLE p Infinite sample image Generated image • Assuming Markov property, what is conditional probability distribution of p, given the neighbourhood window? • Instead of constructing a model, let’s directly search the input image for all such neighbourhoods to produce a histogram for p • To synthesize p, just pick one match at random Slides courtesy of Alyosha Efros Really Synthesizing One Pixel SAMPLE finite sample image p Generated image • However, since our sample image is finite, an exact neighbourhood match might not be present • So we find the best match using SSD error (weighted by a Gaussian to emphasize local structure), and take all samples within some distance from that match Growing Texture • Starting from the initial image, “grow” the texture one pixel at a time • The size of the neighborhood window is a parameter that specifies how stochastic the user believes this texture to be Some Details Growing is in “onion skin” order • Within each “layer”, pixels with most neighbors are synthesized first • If no close match can be found, the pixel is not synthesized until the end Using Gaussian-weighted SSD is very important • to make sure the new pixel agrees with its closest neighbors • Approximates reduction to a smaller neighborhood window if data is too sparse Window Size Controls Randomness More Synthesis Results Increasing window size Brodatz Results reptile skin aluminum wire Failure Cases Growing garbage Verbatim copying Image-Based Text Synthesis Other Texture Synthesis Methods Heeger & Bergen, SIGGRAPH 95 • Early work, got people interested in problem DeBonet, SIGGRAPH 97 • Breakthrough method, surprisingly good results • More complex approach, more parameters (filter banks) Wei & Levoy, SIGGRAPH 99 • Similar to Efros and Leung, but faster • Uses coarse-to-fine, vector quantization Zhu et al., IJCV 98 (and other papers) • Rigorous MRF algorithms, Gibbs sampling • Well-founded statistically, but slower Others... Applications of Texture Modeling Super-resolution • Freeman & Pasztor, 1999 • Baker & Kanade, 2000 Image/video compression Video Textures • Wei & Levoy, 2000 • Schodl et al., 2000 Texture recognition, segmentation • DeBonet Restoration • removing scratches, holes, filtering • Zhu et al. Art/entertainment