Download Statistics

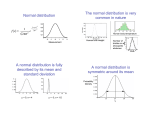
Statistics
Decay Probability
• Radioactive decay is a
statistical process.
– Assume N large for
continuous function
• Express problem in terms of
probabilities for a single event.
– Probability of decay p
– Probability of survival q
– Time dependent
N  N 0 e  t
p  1  e  t
q  e  t
p  q 1
Combinatorics
• The probability that n specific
occurrences happen is the
product of the individual
occurrences.
– Other events don’t matter.
– Separate probability for
negative events
• Arbitrary choice of events
require permutations.
• Exactly n specific events
happen at p:
P  pn
• No events happen except the
specific events:
N n
Pq
• Select n arbitrary events from a
pool of N identical types.
N
N!
  
 n  n!( N  n)!
Bernoulli Process
• Treat events as a discrete trials.
– N separate trials
– Trials independent
– Binary outcome of trial
– Probability same for all
trials.
• This defines a Bernoulli
process.
Typical Problem
• 10 atoms of 42K with a half-life
of 12.4 h is observed for 3 h.
What is the probability that
exactly 3 atoms decay?
Answer
• Probability of 1 decay,
p  1  e t  1  e(t ln 2) / T  0.154
• And 3 arbitrary atoms decay
from the 10 and 7 do not:
10  3 7
P    p q  0.136
3
Binomial Distribution
• The general form of the
Bernoulli process is the
binomial distribution.
– Terms same as binomial
expansion
 N  n N n
Pn    p q
n
• Probabilities are normalized.
N
P
n 0
n
 ( p  q) N  1
mathworld.wolfram.com
Mean and Standard Deviation
• The mean m of the binomial
distribution:
N
N
 N  n N n
m   nPn   n  p q
n 0
n 0  n 
• The standard deviation s of the
binomial distribution:
• Consider an arbitrary x, and
differentiate, and set x = 1.
N
 N  n n N n
N
( px  q)     p x q
n 0  n 
s 2   (n2 Pn  2mnPn  m 2 Pn )
N
Np( px  q ) N 1   nx n 1 Pn
n 0
N
s   n  m 2 Pn
2
n 0
s 2   n2 Pn  2m  nPn  m 2  Pn
s 2  [ N ( N  1) p 2  m ]  2m 2  m 2
s 2  N 2 p 2  Np 2  Np  N 2 p 2
N
Np   nPn  m
n 0
s  Np(1  p)  Npq
Disintegration Counts
• In counting experiments there is
a factor for efficiency e.
– Probability that a
measurement is recorded
p  e (1  e t )
q  1  p  1  e  ee t
Typical Problem
• A sample has 10 atoms of 42K
in an experiment with e = 0.32.
What is the expected count rate
over 3 h?
Answer
• Use the mean of the observable
count, convert to rate.
rc  m / t  Ne (1  e  t ) / t
• 10(0.32)(0.154)/3 h = 0.163 h-1.
More Counts
• Consider a source of 42K with
an activity of 37 Bq, in a
counter with e = 0.32 measured
in 1 s intervals.
• The mean disintegration rate is
just the activity, rd = 37 Bq.
– The count rate is
• What is the mean count rate?
• Decay constant is  = ln2 / T =
0.056 h-1 = 1.55 x 10-5 s-1.
– The probability of decay is
• What is the standard deviation
of the count rate?
rc  erd  11.8 s 1
p  1  e t  1.55 105
• Number of atoms is N = rd / =
2.4 x 106.
s c  Nep(1  ep)  3.4 s1
Poisson Distribution
• Many processes have a a large
pool of possible events, but a
rare occurrence for any
individual event.
– Large N, small n, small p
N
N!
Nn
  

n
  n!( N  n)! n!
• This is the Poisson distribution.
– Probability depends on only
one parameter Np
– Normalized when summed
from n =0 to .
q N n  q N  (1  p) N
N ( N  1) 2
p 
2!
( Np) 2
 1  Np 
   e  Np
2!
q N n  1  Np 
q N n
 N  n N n ( Np) n  Np
Pn    p q

e
n!
n
Poisson Properties
• The mean and standard deviation are simply related.
– Mean m = Np, standard deviation s2 = m, s  m
• Unlike the binomial distribution the Poisson function has values
for n > N.
Poisson Away From Zero
• The Poisson distribution is
based on the mean m = Np.
– Assumed N >> 1, N >> n.
• Now assume that n >> 1, m
large and Pn >> 0 only over a
narrow range.
• This generates a normal
distribution.
• Let x = n – m.
m m  xe m
m m m xe m
Px 

( m  x)! m![( m  x)! / m!]
• Use Stirling’s formula
m! 2mm m e m
Px 
Px 
mx
2m[( m  1)...( m  x)]
1
2m[(1  1 / m )...(1  x / m )]
e x / 2m
Px 

1/ m
x/m
2m[(e )...(e )]
2m
1
2
Normal Distribution
• The full normal distribution
separates mean m and standard
deviation s parameters.
f ( x) 
e  x  m 
2
2 s
/ 2s 2
• Tables provide the integral of
the distribution function.
• Useful benchmarks:
– P(|x - m| < 1 s = 0.683
– P(|x - m| < 2 s = 0.954
– P(|x - m| < 3 s = 0.997
Typical Problem
• Repeated counts are made in 1min intervals with a long-lived
source. The observed mean is
813 counts with s = 28.5
counts. What is the probability
of observing 800 or fewer
counts?
Answer
• This is about -0.45s.
• Look up P((x-m)/s < -0.45)
– P = 0.324
Cumulative Probability
• Statistical processes can be
described for large numbers.
– Can we model one event?
– No two events are equal
• Consider an event with a 500
keV incident photon on soft
tissue with attenuation m =
0.091 cm-1.
• Probability distributions
typically reflect incidence in an
infinitessimal region.
– Integrate over a range
• The probability of an
interaction in 2 cm is
x
Pc   P1 ( x)dx
x
Pc ( x)   memx dx  1  emx
0
• P = 1 – 0.834 = 0.166
0
• How does one simulate this?
Random Numbers
• To simulate a statistical process
one needs a random selection
from the possible choices.
• Algorithms can generate
pseudo-random numbers.
– Uncorrelated over a large
range of trials.
– Randomness limited for
large sets or fixed starts
• Linear Congruential Generator
• Start with a seed value, X0.
– Select integers a, b.
• For a given Xn,
– Xn+1 = (aXn + b) mod m
• The maximum number of
random values is m.
Random Distribution
• A selected random number is
usually generated in a large
range of integers.
– Uniform over the range
• To select a number with a
normal distribution:
– Take two random numbers
R1, R2 from 1 to N.
ri  Ri / N
• Normalize values to select a
narrow range.
– Usually from 0 to 1
– Apply algorithm with m, s
• Convert range to match a
distribution.
– (Box-Mueller algorithm)
x  m  s cos2r1   2 ln r2
Monte Carlo Method
• The Monte Carlo method
simulates complicated systems.
• Use random numbers with
distribution functions to select a
value.
• Test that value to see if it meets
certain conditions.
• Simple Monte Carlo for .
– Select a pair of random
numbers from 0 to 1.
– Sum the squares and count
if it’s less than 1.
– Multiply the fraction that
succeed by 4.
Interaction Simulation
Typical Problem
• A 100 keV neutron beam is
incident on a mouse (3 cm
thick). Calculate the energy
deposited at different depths.
Data Table
• H
m=0.777 cm-1
• O
m=0.100 cm-1
• C
m=0.0406 cm-1
• N
m=0.00555 cm-1
• Total m=0.92315 cm-1
• Simulate one neutron.
• Find the distance of penetration
by inverting the probability.
x
1
mtot
ln 1  ri 
• Find the nucleus struck.
– Normalize the mi to the total
possible mtot.
• Select the energy of recoil and
angle.
• Repeat for new distance.
Fitting Tests
• Collected data points will approximate the physical
relationship with large statistics.
• Limited statistics require fits of the data to a
functional form.
Least Squares
• Assume that the data fits to a
straight line.
y  ax  b
Q 1

a N
 2 y
x y
 a x 2j  b x j
j
• Use a mean square error to
determine closeness of fit.
1
Q
N

1
N
 y
N
j 1
 y
j  y( x j )

2
 ax j  b 
2
j
• Minimize the mean square
error.
j
Q
1

b
N
y
a
b
j
j
 ax j  b  x j   0
 2y
j
 x j  b  0
 a x j   b  a x j  Nb
N  x j y j   x j  y j 
N  x 2j   x j 
2
1
N
y
j

a
N
x
j
Polynomial Fit
• The procedure for a least
squares fit applies to any
polynomial.
– n+1 parameters ak
y ( x j )   ak x kj
• Minimize error expression Q.
n
1 N 

Q    y j   ak x kj 
N j 1 
k 0

n
k 0
2
n
Q 2 N 
k
m 
   y j   ak x j   x j   0
am N j 1 
k 0



• Requires simultaneous solutions
to a set of n+1 equations.
x
j
m
j

y j   ak x kj x mj   ak  x kj  m
k
j
k
j
Exponential Fit
• The least squares fit can be
applied to other functions.
• For a single exponential a fit
can be made on the log.
y  aebx
ln y  ln a  bx
n
y ( x )   ak e bk x
• For the sum of exponentials
consider constants a, b.
– Select initial values
– Taylor’s series to linearize
– Find hk that minimize Q
k 1
y
hk
k 1 bk
n
y( x j ; bk )  y( x j ; bk 0 )  
bk  bk 0  hk
Chi Squared Test
• Fitting is based on a limited
statistical sample.
• A chi-squared test measures the
data deviation from the fit.
– Normally distributed
– Mean k for k degrees of
freedom
• Divide the sample into n classes
with probabilities pi and
frequencies mi.
n
mi  Npi 2
i 1
Npi
s  
• The test is
k  1  s2
(
, )
2
2
2
2
P(    s ) 
k 1
(
,0)
2

(a, x)   t a 1et dt
x