Download Document

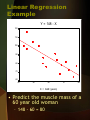
Introduction to
Biostatistics
Jane L. Meza, Ph.D.
Outline
• Hypothesis testing
– Comparing 2 groups
•
•
•
•
Paired t-test
2 Independent Samples t-test
Wilcoxon Signed Ranks test
Wilcoxon Rank Sum test
– Comparing 3 or more groups
• ANOVA
–
–
–
–
One-Way
Bonferroni Comparisons
Repeated Measures
Kruskal-Wallis
• Chi-square
• Regression
– Linear Correlation
– Linear Regression
Deck of Cards
• If you randomly select a card,
what is the probability the card
is red?
• If we draw 10 cards, how many
of the 10 cards do we expect to
be red?
• Are we guaranteed that 5 of the
cards will be red?
Deck of Cards
Experiment
• Is it possible that we could
draw 10 red cards in a row
from a standard deck of
cards?
• Is it very likely that we could
draw 10 red cards in a row
from a standard deck of
cards?
• We have conflicting
information – we assumed
that 50% of the cards were
red, but in our sample 100%
of the cards were red. What
should we conclude?
Experiment
• Why did you make that
conclusion?
• What assumptions are you
making?
• Is there a possibility that
your conclusion is
incorrect?
Hypothesis Testing
• Start with an assumption
(Null Hypothesis)
– 50% of the cards are red
• Gather data
– Draw 10 cards
Hypothesis Testing
• Find the probability of the
results under your
assumptions
– Find the probability of
drawing 10 red cards in a row,
assuming that 50% of the 52
cards are red.
– Probability of drawing 10
cards in a row is highly
unlikely if 50% of the 52 cards
are red (<0.001).
Hypothesis Testing
• State your conclusion.
– Either we experienced a rare
event, or one of our
assumptions is incorrect.
– Since the probability of
drawing 10 red cards in a row
is so small, we conclude that
our assumptions are probably
incorrect.
– We conclude that more than
50% of the cards are red.
Hypothesis Testing
Example:
Is There a Difference?
• Compare treatments or groups
• Psoriasis Example:
– Some studies have suggested that
psoriasis is more common among
heavy alcohol drinkers.
– Case-control study of men age 19-50.
(Poikolainen et al Br Med J 1990; 300:780-783)
– Cases were men who had psoriasis.
– Controls were men who did not have
psoriasis.
– All subjects completed
questionnaires regarding life style
and alcohol consumption.
– Is the mean alcohol intake for men
with psoriasis (cases) greater than
men without psoriasis (controls)?
– Cases: mean=43, SD=85.8, n=142
– Controls: mean=21, SD=34.2, n=265
Hypothesis Testing:
Is There a Difference?
• Null Hypothesis: HO
– Often a statement of no
treatment effect
– Example 1: The proportion of
red cards is the same as the
proportion of black cards
(50%).
– Example 2: There is no
association between alcohol
intake and psoriasis. In other
words, the mean alcohol
intake for men with psoriasis
is the same as the mean
alcohol intake for men
without psoriasis.
Hypothesis Testing:
Is There a Difference?
• Alternative Hypothesis: HA
– May be one-sided or two-sided
– Example 1:
• One-sided: The proportion of
red cards is larger than the
proportion of black cards.
• Two-sided: The proportion of
red cards is different than the
proportion of black cards.
– Example 2:
• One-sided: Mean alcohol intake
for cases (with psoriasis) is
larger than mean alcohol intake
for controls (without psoriasis)
• Two-sided: Mean alcohol intake
for cases is different than the
mean alcohol intake for controls
Hypothesis Testing:
Conclusions
• The null hypothesis is
assumed true until
evidence suggests
otherwise.
• 2 possible conclusions:
– Reject the null hypothesis
in favor of the alternative.
– Do not reject the null
hypothesis.
Hypothesis Testing:
Errors
DECISION
Do not
Reject HO
TRUTH
HO is True
HO is False
Reject HO
Type I
Correct
Error (a) Decision
Correct
Decision
Type II
Error (b)
• Significance level: a
– Probability of rejecting a true null
hypothesis
• b:
– Probability of not rejecting a false
null hypothesis
• Power: 1-b
– Probability of detecting a true
difference
Hypothesis Testing:
Steps
• Assume the null hypothesis is
true.
• Determine a test statistic
based on the observed data.
• Using the test statistic, how
likely is it that we observe
the outcome or something
more extreme if the null
hypothesis is true?
• If the test statistic is unlikely
under the null hypothesis, we
reject the null hypothesis in
favor of the alternative
hypothesis.
Hypothesis Testing:
P-value
• Measures how likely is it that
we observe the outcome or
something more extreme,
assuming the null hypothesis is
true.
• Small p-value is evidence
against the null hypothesis and
we reject the null hypothesis.
• Large p-value suggests the
data are likely if the null
hypothesis is true and we do
not reject the null hypothesis.
Hypothesis Testing:
P-value Method
• If p < a, Reject the null in
favor of the alternative.
• If p ≥ a, Do Not Reject the
null.
• p < .05 is generally considered
statistically significant.
• Determining the p-value
requires making assumptions
about the data.
Hypothesis Testing:
Psoriasis Example
• Ho: There is no association
between alcohol intake and
psoriasis.
• Ha: The mean alcohol intake
is different for cases and
controls.
• Using the test statistic, the pvalue was .004.
• Conclusion: Since the p-value
is less than 0.05, Reject Ho.
• There is evidence that the
mean alcohol intake is higher
for cases (mean=43) than
controls (mean=21).
Hypothesis Testing:
Antihypertensive Example
• Aim: Compare two
antihypertensive strategies
for lowering blood pressure
– Double-blind, randomized
study
– Enalapril + Felodipine vs.
Enalapril
– 6-week treatment period
– 217 patients
• Outcome of interest:
diastolic blood pressure
• Based on AJH, 1999;12:691696.
Hypothesis Testing:
Antihypertensive
Example
• After 6 weeks of therapy, the
average change in DBP was:
10.6 mm Hg in the Enalapril +
Felodipine group (n=109, SD=8.1)
compared to
7.4 mm Hg in the Enalapril group
(n=108, SD=6.9)
• The authors used a hypothesis
test to help determine which
therapy was more effective.
Hypothesis Testing:
Antihypertensive
Example
• Statement from AJH
– “The group randomized to 5 mg
enalapril + 5 mg felodipine had a
significantly greater reduction in
trough DBP after 6 weeks of blinded
therapy (10.6 mm Hg) than the
group randomized to 10 mg
enalapril (7.4 mm Hg, P<0.01).”
– What does P<0.01 mean?
• Assuming that the 2 therapies are
equally effective, there is less
than a 1% chance that we would
have observed treatment
differences as large or larger
than what was observed.
Hypothesis Testing
• Parametric methods make
assumptions about the
distribution of the observations.
• Non-parametric methods do not
make assumptions about the
distribution of the observations.
• The distribution of the data and
the design of the study should be
carefully considered when
choosing the statistical test to be
used.
Comparing 2 Groups Continuous Data
Paired Data
• For each observation in the first
group, there is a corresponding
observation in the second group.
• Example: “Before and After”
• Example: Subjects age/sex matched
• Pairing eliminates some of the
variability among individuals,
since measurements are made
on the same (or similar)
subjects.
• Paired groups are called
dependent.
Comparing 2 Groups Continuous Data
Paired t-test
• Two paired groups
• Sample size is large (30 or
more pairs)
Normal Distribution
• Data follows a
normal
distribution if
the histogram is
approximately
symmetric and
bell shaped.
• Described by two
parameters
– mean (m)
– SD (s)
Normal Distribution
• Z-score measures how many SDs
an observation is away from the
mean
• Z=(x-m)/s
• About 95% of the values fall
within 2 SDs of the mean
Comparing 2 Groups Continuous Data
Paired t-test Example
• In 40 subjects, blood pressure was
measured before and after taking
Captopril.
• Outcome of interest: change in
blood pressure after taking the
drug
• HO: No association between
Captopril and blood pressure.
• HA: Mean blood pressure is lower
after patients take Captopril.
• P-value < .001.
• Reject HO in favor of HA. There is
evidence that mean blood pressure
is lower after taking Captopril.
–
Based on MacGregor et al., British Medical Journal, Vol. 2
Comparing 2 Groups Continuous Data
Wilcoxon Signed Ranks Test
• Two paired groups
• Sample size is small (less
than 30 pairs).
• Wilcoxon Signed Ranks Test
compares medians rather
than means.
• Non-parametric test.
Comparing 2 Groups Continuous Data
Wilcoxon Signed Ranks Test Example
• In 10 postcoronary patients, maximum
oxygen uptake was measured before and
after a 6 month exercise program.
• Outcome of interest: change in oxygen
uptake after a 6 month exercise program
Difference in Maximum Oxygen Uptake
Before and After Exercise Program
5
4
3
Frequency
2
1
Std. Dev = 8.10
Mean = -5.2
N = 10.00
0
-20.0
-15.0
-10.0
-5.0
0.0
5.0
Difference in max. oxygen uptake ml/(kg)(min)
Comparing 2 Groups Continuous Data
Wilcoxon Signed Ranks Test
Example
• HO: There is no association
between exercise and
oxygen uptake.
• HA: Median oxygen uptake is
higher after exercise
program.
• p-value =.09.
• Do not reject HO. There is
not enough evidence to
conclude that oxygen uptake
is higher after the exercise
program.
Comparing 2 Groups Continuous Data
Independent Samples t-test
• Two independent groups
• Sample size is large (30 or
more in each group).
Comparing 2 Groups Continuous Data
Independent Samples t-test
Example
• 30 women with pregnancyinduced hypertension are given
low-dose aspirin
• 42 women with pregnancyinduced hypertension given a
placebo
• Outcome of interest: blood
pressure
–
Based on Schiff, E et al., Obstetrics and Gynecology, Vol 76,
Nov 1990, 742-744.
Comparing 2 Groups Continuous Data
Independent Samples t-test
Example
• HO: No association between
low-dose aspirin and blood
pressure.
• HA: Mean blood pressure is
lower for the aspirin group
• P-value = .15.
• Do not reject HO. There is
not enough evidence to
conclude that the mean blood
pressure is lower for the
aspirin group.
Comparing 2 Groups Continuous Data
Wilcoxon Rank Sum Test
• Two independent groups
• Sample size is small (less
than 30).
• Wilcoxon Rank Sum Test
compares medians rather
than means
• Nonparametric test
Comparing 2 Groups Continuous Data
Wilcoxon Rank Sum Test Example
• 13 patients were randomized to
placebo
• 15 take randomized to receive calcium
supplements
• Outcome of interest: blood pressure
• HO: No association between calcium
supplements and blood pressure.
• HA: Median blood pressure in calcium
supplement group is different than
placebo group.
• P-value =.79.
• Do not reject HO. There is not enough
evidence to conclude that median
blood pressure for the calcium group is
different than the placebo group.
–
Based on Lyle et al., JAMA, Vol 257, No 13.
Comparing 3 or more
groups
• Chi-square Test for categorical
data
• Analysis of Variance (ANOVA) for
continuous data
• Common uses:
– Compare an outcome for 3 or more
treatments
– Compare a characteristic in 3 or
more populations
Chi-Square Test
• Compare 2 or more groups
• Categorical data
• Example: To study effectiveness
of bicycle helmets, individuals
who were in an accident were
studied.
• Outcome of interest: Compare
proportion of persons suffering a
head injury while wearing a
helmet to proportion of persons
suffering a head injury while not
wearing helmet
Chi-Square Test
2x2 Table
Wearing Helmet
Injury
Yes
No
Yes
No
17 (12%)
130 (88%)
218 (34%)
428 (66%)
Total
147
646
• 12% (17/147) of those wearing a
helmet had a head injury
• 34% (218/646) of those not
wearing a helmet had a head
injury
Chi-Square Test
• Ho: The proportion suffering a head
injury is the same for accident victims
who wore helmets vs. accident victims
who did not wear helmets.
• Ha: The proportion suffering a head
injury is different for accident victims
who wore helmets vs. accident victims
who did not wear helmets.
• p-value < .001
• Conclusion: Reject Ho. The
proportion of individuals suffering
head injuries was higher for accident
victims who did not wear helmets
(34%) compared to those who did wear
helmets (12%).
• Among persons in an accident, wearing
a helmet appears to lower incidence of
head injury
ANOVA
(Analysis of variance)
• Used to compare a
continuous variable among
three or more groups
• HO: The group (or
treatment) means are the
same.
• HA: At least one mean is
different from the others.
One-Way ANOVA
• One factor (characteristic)
is being studied
– Example: treatment group
• Placebo
• experimental treatment 1
• experimental treatment 2
• 3 or more independent
groups
• The distribution for each
group is not heavily skewed.
• Group variances or sample
sizes are approximately
equal.
One-Way ANOVA
Example
• Aim: Compare microbiological
growth under 3 different CO2
pressure levels.
• Factor of interest: 3 different CO2
pressure levels
• Outcome of interest: average
microbiological growth in each
treatment group
• HO: The mean microbiological
growth for the 3 treatments (CO2
level) is the same
• HA: At least one of the means is
different.
• p-value = .001
• Reject HO in favor of HA. There is
evidence that mean growth is
different for the three treatment
groups.
One-Way ANOVA
Example
• Mean microbiological
growth under 3 different
CO2 pressure levels.
– Group 1 mean: 56.2
– Group 2 mean : 22.5
– Group 3 mean: 26.1
Bonferroni
Comparisons
• Use when ANOVA yields a
significant p-value.
• If we perform several t-tests
to compare each pair of
means, the probability of a
Type I error is > 5%.
• The Bonferroni method
modifies the p-value to
account for multiple
comparisons so that, overall,
the probability of making a
Type I error is 5%.
Bonferroni Comparisons
Example
• Is the mean for group 1 different from
the mean for group 2?
– P=.001
– Conclusion: The mean for group 1 is
different from the mean for group 2.
• Is the mean for group 1 different from
the mean for group 3?
– P=.02
– Conclusion: The mean for group 1 is
different from the mean for group 3.
• Is the mean for group 2 different from
the mean for group 3?
– P=.34
– Conclusion: The mean for group 2 is
different from the mean for group 3.
• Therefore, the difference in the 3
group means can primarily be explained
by the higher mean for group 1
compared to groups 2 and 3.
Repeated Measures
ANOVA
• Subjects are measured at
more than one time point
• Since multiple
measurements are taken for
the same subject over time,
the observations are not
independent
Repeated Measures
ANOVA Example
• 12 rabbits receive in random
order 3 different dose levels of a
drug to increase blood pressure,
with a washout period between
treatments.
• Outcome of interest: average
blood pressure for the three
dose levels
• HO: Average blood pressure is
the same for the 3 dose levels
• HA: At least one of the means is
different.
• P=.01
• Reject HO. There is evidence of
a difference in mean blood
pressure for the 3 dose levels.
Kruskal-Wallis ANOVA
• Nonparametric ANOVA
• Use when the distribution
for one or more groups is
heavily skewed.
Linear Regression
Y = 148 - X
120
110
100
90
80
70
60
40
50
60
70
80
X = AGE (years)
• Is there a linear relation between 2 continuous
variables? If so, what line best fits the data?
• Use the line to predict a value for a new
observation
– Example: Can we predict muscle based on a
woman’s age?
• Explore relationship between 2 numerical
variables
– Example: What is the relation between
muscle mass and age?
Linear Correlation (r)
Is There an Association?
• Measures linear relationship
between 2 continuous variables.
• Interpreting r :
Absolute
Value
of r
0 - .25
.25 - .50
.50 - .75
.75 – 1.0
Linear
Relationship
poor
fair
good
very good
Linear Correlation (r)
Examples
r=0
r = .55
r = .85
r = -.85
Linear Correlation (r)
Examples
r=1
r = -1
Linear Regression
Least Squares Regression
Line
• Estimate the best line to fit
the data
• Y = b0 + b1X
– Y is the dependent variable
• Example: Muscle mass
– X is the independent variable
• Example: Age of woman
– b0 is the intercept
– b1 is the slope
Linear Regression
Example
Y = 148 - X
120
110
100
90
80
70
60
40
50
60
70
80
X = AGE (years)
• Predict the muscle mass of a
60 year old woman
– 148 - 60 = 80
Linear Regression Example
Y = 148 - X
120
110
100
90
80
70
60
40
50
60
70
80
X = AGE (years)
• On average, what is the difference in
muscle mass for women who differ in
age by 1 year?
– b1 = -1
– For women whose age differs by
one year, we expect the average
muscle mass will be one unit
lower for the older women
Linear Regression
Notes
• Significant correlation does
not necessarily imply
causation.
• Do not use a line to predict
new observations if there is
not significant linear
correlation.
• When predicting new
observations, stay within
the domain of the sample
data.
References
• Dawson-Saunders, B and Trapp RG (1994). Basic
and Clinical Biostatistics. Appleton and Lange.
Norwalk, CT.
• Lane, DM. (2000). Hyperstat Online. On-line text,
www.statistics.com.
• MacGregor GA, Markandu ND, Roulston JE and Jones
JC (1979). “Essential Hypertension: Effect of an
Oral Inhibitor of Angiotensin-Converting Enzyme”.
British Medical Journal, Nov 3; Vol 2, 1106-9.
• Neter, J., Wasserman W. and Kutner, MH. (1990).
Applied Linear Statistical Models. Irwin. Burr
Ridge, IL.
• Pagano M and Gauvreau, K. (1993). Principles of
Biostatistics. Duxbury Press. Belmont, CA.
• Schiff E, Barkai G, Ben-Baruch G and Mashiach S.
(1990). “Low-Dose Aspirin Does Not Influence the
Clinical Course of Women with Mild PregnancyInduced Hypertension”. Obstetrics and
Gynecology, Vol 76, November, 742-744.
• Swinscow, TDV. (1997). Statistics at Square One.
BMJ Publishing Group. On-line text,
www.statistics.com.
• Triola MF (1998), Elementary Statistics. AddisonWesley. Reading, MS.