Download Chapter 8: The Binomial Distribution and The Geometric Distribution

Chapter 8:
The Binomial Distribution
and
The Geometric Distribution
“In God we trust. All others must bring data.”
Robert Hayden,
Plymouth State College
8.1 The Binomial Distributions
(pp. 414 – 432)


The Binomial distribution is frequently useful
in situations where there are two outcomes of
interest, such as SUCCESS or FAILURE.
It is often used to model real-life situations,
and it finds its way into many extremely
useful and important statistical applications
and computations.
The Binomial Setting
1.
2.
3.
4.
Each observation is in one of two
categories: success or failure
There is a fixed number, N, of observations.
Observations are independent. Knowing the
result of one observation tells you nothing
about the other observations.
The probability of success is the same for
each observation.
If a count, X, has a binomial distribution
with N number of observations and p of
success, then:
Mean  X    X  N p
standard deviation  X    X  N p 1  p 
The probability that one will get exactly k successes is
Ck p 1  p 
k
N
N k
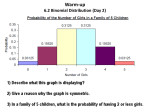
Example: Die is rolled 60 times.
X = number of times a “3” is rolled:
1
 X  60    10
6
 1  5 
 X  60      2.89
 6  6 
The probability that exactly ten "3's" will be rolled:
10
1 5
60 C10 
  
6
  6
50
 .1370  13.7%
1


On the TI83+, binompdf 100, ,10   .1370  13.7%
6


Another example: small sample size
from large population.


Use of binomial distribution is appropriate.
Assumption:



30% of a population is Hispanic
Random sample of size 4 is chosen from the
population
If X is the number of Hispanics in the sample
then:
   4  0.3  1.2
X
X 
 4 .3 .7   .9165
Pr  X  0   4 C0  .3  .7   0.2401
0
4
Pr  X  1  4 C1  .3  .7   0.4116
1
3
Pr  X  2  
Pr  X  3 
Pr  X  4  
The probability tha a sample would contain two or fewer Hispanics is
Pr  X  0   Pr  X  1  Pr  X  2   _________
Using the TI83+:

The probability that the sample contains
exactly 2 Hispanics is


Binompdf(4, .3, 2) = .2646
The probability that the sample contains 2 or
fewer Hispanics is

Binomcdf(4, .3, 2) = .9163
It is important to understand when one has a
binomial setting and when one does not.

Consider a shuffled deck of 52 playing cards:







Example #1: random card is selected; suit is noted (is it a
heart or not); then card is replaced
Cards shuffled with random card selected; suit is noted (is
it a heart or not); then card is replaced
Entire process is repeated 8 more times for a total of 10
random selections
X = total number of hearts obtained in 10 trials
Binomial setting? Why?
X = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
N =10 p = 0.25 AND each observation is INDEPENDENT of
the other
It is important to understand when one has a
binomial setting and when one does not.

Consider a shuffled deck of 52 playing cards:





Example #2: random card is selected; suit is
noted (is it a heart or not); then card is NOT
replaced
Cards shuffled with random card selected; suit is
noted (is it a heart or not); then card is NOT
replaced
Entire process is repeated 8 more times for a total
of 10 random selections
X = total number of hearts obtained in 10 trials
Binomial setting? Why NOT?
8.2 The Geometric Distributions
pp. 434 – 444



The AP Syllabus states that you only need to
know how to obtain geometric probabilities
through simulation.
The geometric setting is somewhat similar to
that of the binomial.
The basic difference is that the geometric
setting DOES NOT HAVE A FIXED NUMBER
OF OBSERVATIONS.
The Geometric Setting
1.
2.
3.
4.
Each observation is in one of two
categories: success or failure
The probability of success is the same for
each observation.
Observations are independent. Knowing the
result of one observation tells you nothing
about the other observations.
The variable of interest is the number of
trials required to obtain the first success.
Example: How many times would you expect
to have to roll a single die to get a “6” ?

Simulate 10 trials using TI83+: randint(1, 6, 10)











Trial 1:
Trial 2:
Trial 3:
Trial 4:
Trial 5:
Trial 6:
Trial 7:
Trial 8:
Trial 9:
Trial 10:
The mean of rolls for the 10 trials is _________
If p is the probability of success, and q =1 – p
is the probability of failure, then:




p = probability of success on first trial
qp = probability of success on second trial
q^2(p)=probability of success on the third trial, etc.
If X is a variable representing the number of trials
until the first success, the expected value of X is
 X  1 p  2qp  3q p  4q p  ....
2

3
 p 1  2q  3q  4q  ...
2
3

Observe that:
1  2q  3q 2  4q3  ...


 1  q  q 2  q3  ... 1  q  q 2  q3  ...


Also, for 0<q<1, the sum of the infinite series


1
1  q  q  q  ... 
1 q
2
3
 X  p 1  q  q 2  q 3  ... 1  q  q 2  q 3  ... 
 1  1 
p
p 1
 p
 2


2
p
p
 1  q   1  q  1  q 
The probability of rolling a “6” is 1/6.
The expected number of rolls before the first
success is 1/(1/6) = 6.

California Lottery:





You choose 6 numbers for {1, 2, 3, …,49, 50, 51}
The state randomly selects 6 numbers
You win $1 million if your 6 match the 6 selected by the state
Your probability of matching all six is
1
1

18009460
51 C6
So you would expect your first success after playing 18,009,460
times or after 346,336 weeks (6660 years) if you play once a
week.