* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download (1) limits of hearing
Survey
Document related concepts
Audiology and hearing health professionals in developed and developing countries wikipedia , lookup
Speech perception wikipedia , lookup
Noise-induced hearing loss wikipedia , lookup
Sound localization wikipedia , lookup
Olivocochlear system wikipedia , lookup
Auditory system wikipedia , lookup
Transcript
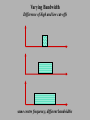
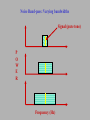
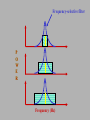
Hearing Outline (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception (1) Limits of hearing a) audibility function b) detection of complex stimuli c) masking & the critical band d) patterns of hearing loss range of hearing is 20 - 20,000 Hz How good is the ear at detecting sounds? How GOOD is the ear at detecting sounds? We can present complex stimuli by breaking up pure tones. Acoustic power can be concentrated into a single frequency (i.e., a pure tone). P O W E R Or distributed among multiple frequencies presented simultaneously (i.e., a complex tone). bandwidth low high Frequency (Hz) In addition, we can vary the bandwidth (i.e., the difference between the highest and lowest frequencies) in the complex tone. How does detectability of a sound depend on complexity? (1) when frequencies are close together (narrow bandwidth) detectability depends on the total acoustic power in the stimulus the acoustic power is summed across frequencies. (2) when the frequencies are far apart (wide bandwidth) detectability declines when the frequency components in a complex tone are too far apart the auditory system is no longer capable of combining their acoustic power. The bandwidth at which the integration begins to fail is called the critical bandwidth. Detection of Complex Stimuli nearby frequencies are combined % detection close together far apart critical bandwidth stimulus bandwidth frequencies falling within a critical bandwidth are integrated by the auditory system Noise Masking (1) broad-band noise contains all audible frequencies (“white noise”) (2) band-pass noise contains a smaller range of frequencies low frequency cut-off Power high frequency cut-off centre frequency Frequency (Hz) (3) bandwidth is the difference between the high and low frequency cutoffs. Varying Bandwidth Difference of high and low cut-offs same centre frequency, different bandwidths What does noise sound like? depends on bandwidth (1) a very narrow band noise sounds like a tone (centre frequency) (2) white noise is a hissing sound (no pitch) Detecting a signal embedded in noise How does noise affect pure tone thresholds? Consider a task in which you are asked to detect a pure tone (the signal) embedded in a background noise. (1) The noise is band-pass: the centre frequency equals the signal's frequency. (2) The bandwidth of the noise varies across experimental conditions. How does detectability vary with noise bandwidth? Noise Band-pass: Varying bandwidths Signal (pure tone) P O W E R Frequency (Hz) Detecting a signal embedded in noise Threshold How does noise affect pure tone thresholds? critical bandwidth no noise Noise Bandwidth threshold increases with noise bandwidth up to a point, then levels off Detecting a signal embedded in noise How does noise affect pure tone thresholds? (1) Increasing bandwidth does increase detection threshold. • this increase in threshold is referred to as masking. • we say that the signal is masked by the noise. (2) Increasing noise bandwidth results in more masking, but only up to a point. • beyond some critical bandwidth, increasing noise bandwidth does not result in more masking. • The amount of masking levels off and thresholds are constant. Interpretation of noise masking The critical band usually is interpreted as the width of an frequency-selective auditory channel/filter. • detect signal by monitoring response of 1 channel • noise falling within channel masks signal • noise falling outside channel has no effect (1) This filter responds well to a small range of auditory frequencies. (2) Analogous to the spatial frequency channels. Frequency-selective filter P O W E R Frequency (Hz) Frequency-selective filters (or channels) (1) The assumption is that observers have many auditory channels tuned to different frequencies. (2) Some channels respond to low frequencies, some to high frequencies, some to medium frequencies. (3) In all cases, the auditory filter responds to a small range around a preferred, or best frequency. (4) Generally, the critical band increases with increasing frequency. Hearing Loss Two types: (a) conduction loss (b) sensory/neural loss Conduction hearing loss Disorder of outer and/or middle ear • problem associated with mechanical transmission of sound into cochlea Causes: • blockage of outer ear • punctured eardrum • middle ear infection • otosclerosis Effects: • broad-band sensitivity loss • conduction loss can be severe (up to 30 dB) • loss occurs across a wide range of frequencies • does not affect neural mechanisms • treated with hearing aids/surgery (stapedectomy) Sensory/Neural Loss Damage to the cochlea and auditory nerves • age-related hearing loss (Presbycusis) • progressive sensitivity loss at high frequencies • high frequency cutoff drops from 15,000 Hz (30 years) to 6,000 Hz (70 years) Effects of Exposure to Noise (1) Temporary Thresholds Shifts (TTS) • short term exposure to noise (nightclub, concert) • increases your thresholds about 30 dB • recover over a period of several hours/days (2) Permanent Thresholds Shifts (PTS) • long term exposure to noise (work-related) • short, intense sounds (explosion) • can be as large as 60 dB (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception Loudness Loudness is a psychological, not physical, attribute of sound! • loudness is not the same as intensity (it is your subjective perception of intensity) • cannot measure loudness with a sound meter How can we estimate loudness? (1) Loudness Matching Method (2) Magnitude Estimation Method Loudness Matching Method Task: Match the loudness of 2 tones. (1) present a standard tone at a fixed intensity (2) present a test tone at a different intensity (3) adjust test's intensity until it has the same loudness as the standard (4) repeat procedure for many test frequencies (5) graph of intensities at all test frequencies (6) repeat entire procedure for a new standard intensity Equal Loudness Contour every point on the contour has the same loudness as the standard Equal Loudness Contours • When the standard intensity is low, equal loudness contours have the same shape as the audibility function. • When the standard intensity is high, equal loudness contours are much flatter than the audibility function. Another way of stating the results: • At low intensities tones have the same loudness when they are equally detectable • At high intensities they match in loudness when they have the same intensity. Magnitude Estimation In a magnitude estimation task, an observer rates the loudness of a stimulus on a numerical scale. (We are really good at this!) The loudness ratings are related to intensity according by the formula: Loudness = k * Intensity0.67 (Steven’s Power Law) Loudness Loudness grows more slowly than intensity! Intensity (dB) Effects of noise mask on loudness Consider a task in which observers rate the loudness of a pure tone signal embedded in a band-pass noise centred on the signal frequency. Noise will mask the target, so we would expect to find that loudness ratings are decreased for low intensity signals. Q: What happens at higher intensities, when the signal is above threshold? A: Once above threshold, loudness increases rapidly -- much more rapidly than normal. Effects of noise mask on loudness This figure shows loudness judgements for a 1,000 Hz tone presented in quiet (left curve) and in 2 different amounts of noise (middle and right curves). Note how all the curves converge at high intensities. This abnormally rapid growth in loudness with increasing intensity is referred to as loudness recruitment. Effects of hearing impairment on loudness Some forms of hearing loss (cochlear defects) affect loudness judgements in much the same way as a masking noise: loudness for weak, but not intense, tones is reduced. This phenomenon is another example of loudness recruitment. Loudness of Complex Tones complex tones vs. pure tones Complex tones are sometimes louder than pure tones of equal energy. Differences depend on the bandwidth of the complex stimulus. Zwicker, Flottorp, & Stevens (1957) compared loudness of pure tone (1,000 Hz) vs. complex tone (made up of frequencies ranging from 900 to 1,100 Hz) listeners adjusted the intensity of the pure tone to match loudness of complex tone experimenters varied the bandwidth of the complex tone all complex tones had equal energy Effect of bandwidth on loudness loudness changes at critical bandwidth Intensity of matching tone 160 Hz Stimulus Bandwidth (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception Pitch Pitch is also a psychological, not physical, attribute of sound! • pitch is not the same thing as frequency (it is your subjective perception of frequency!) • low frequencies (e.g., 500 Hz) will sound low in pitch • high frequencies (e.g., 1500 Hz) will sound high in pitch Place Theory of Pitch (of pure tones) • peak activity is localized on basilar membrane • different frequencies => different locations • pitch is encoded by the place of activation Pros (1) damaging parts of basilar membrane results in frequencyspecific deficits (2) stimulating parts of basilar membrane evokes different pitches Cons (1) low frequencies have a pitch, but don’t produce localized activity on basilar membrane (2) Can’t account for pitch of complex sounds Frequency Theory of Pitch • pitch depends on rate, not place, of response • neurons can fire in-synch with signals • rate of response might represent frequency of stimulus But…. cells can’t track high frequency sounds Maybe there is a dual coding theory of pitch! (place theory for high frequencies, response rate for low frequencies) Pitch of Complex Sounds • most sounds are complex • not all complex sounds have a pitch (white noise) • those that do tend to have a harmonic structure Pure Tone low Complex Sound (with pitch) high low high Frequency (Hz) pitch of the complex stimulus = pitch of fundamental frequency Fundamental Frequency The fundamental frequency of a set of frequencies is the highest common divisor of the set. What is the fundamental frequency for each of the following sets? 200, 400, 600, 800, 1000 Hz 200, 600, 800, 1000 Hz 100, 400, 600, 800, 1000 Hz 200, 300, 600, 800, 1000 Hz Each of the above sets has one fundamental frequency, although the fundamental itself may not actually be present in the set. Problem of the Missing Fundamental (Virtual Pitch) Is the fundamental really missing? When the fundamental is missing from the stimulus, do distortions produced by the ear introduce a fundamental frequency? Is the fundamental really missing? effect of masking on virtual pitch Intensity (dB) band-pass mask centred on the fundamental frequency 100 200 300 400 600 800 1000 Frequency (Hz) masking does not eliminate the pitch! (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception Perceptual Organization How do you group sounds to identify an object? Auditory Scene Analysis Gestalt grouping principles apply! (1) Good continuation: spectral harmonics • harmonics are grouped together • doe-rae-mi-fa-so-la-ti-doe (2) Similarity: common spectral content • similar frequencies are grouped together (3) Proximity: common time course • frequencies that occur at the same time are grouped together (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception Cone of Confusion Binaural cues do not provide unambiguous information about a sound's location. For example, the same binaural cues are produced by sounds directly in front of and behind an observer. A particular combination of IIDs and ITDs can be produced by sounds in many different directions. All such directions lie on the surface of the socalled cone of confusion. Minimizing Mislocalizations Even though binaural cues are ambiguous, we don't make very many localization errors. How does the auditory system minimize mislocalizations? (1) Head movements • Only one sound source location is consistent with multiple head positions. (2) Pinna (3) Visual cues Cocktail Party Effect You can focus on one sound in a noisy environment. This form of "sound segregation" is due in part to being able to tell from where the sound is coming. Binaural unmasking • masking reduced when sounds come from different locations Example of how binaural cues reduce masking: (1) Present signal with noise over headphones to the left ear • you can't hear signal (2) now add identical noise (via headphones) to the right ear • even though there is more noise, you now can hear the signal! • binaural unmasking occurs because the noise and signal have different perceived locations (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception Speech Perception Speech perception different from perception of other auditory stimuli. Evidence: (1) Psychophysical experiments demonstrating categorical nature of speech perception. (2) Hemispheric differences in auditory processing: • left hemisphere specialized for speech and language • right hemisphere seems to be more responsive for non-speech sounds Categorical Perception look more closely at physical/acoustic properties of speech signal sound spectrogram: picture of distribution of acoustic energy /da/ /ga/ (Hz) /ba/ (ms) density or darkness: amplitude (loudness) Formants: bands of energy - due to resonances of vocal tract /ba/ /da/ /ga/ f3 f2 f1 rising transition falling transition Manipulation: constant series of 13 syllables that differ only in f2 transition Task: present to subjects for identification - many presentations Identification function: rapid change in identifying function suggests subjects have learned category Conclusions: (1) /ba/, /da/, /ga/ (and other phonemes) are perceived categorically, unlike non-speech sounds (2) main cue: f2 transition Speech Perception Neurons in the auditory cortex are specific for speech sounds. For example: /ba/ /pa/ /ta/ and /da/. There is evidence that these neurons compose ‘speech-selective’ channels. Adaptation!!!! Pre-adaptation: listener had to identify an ambiguous sound as either /da/ or /ta/ (50% chance of choosing either one). Adaptation: listen to /da/ over and over again. Post-adaptation: listen to ambiguous sound again. Result: listeners will identify the ambiguous sound as /ta/. The /da/ channel was fatigued. The End (1) limits of hearing (2) loudness (3) pitch (4) perceptual organization (5) localization (6) speech perception