Download Using PHStat2 to Find Normal Probabilities

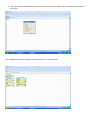
MATH-1410
C. Haugen
Using PHStat2 to find Normal Probabilities
Refer to problem 17 on page 253 of the text. Researchers were interested in the number of hours per week adults in
the United States spend on their home computers. The results of the survey showed that the number of hours were
normally distributed with a mean of 7 hours and a standard deviation of 1 hour. We are asked to find the following:
a) The probability that the hours spent on the home computer by a randomly selected participant are less than 5
hours per week.
b) The probability that the hours spent on the home computer by the participant are between 5.5 and 9.5 hours
per week.
c) The probability that the hours spend on the home computer by the participant are more than 10 hours per
week.
d) Let’s throw one more in – What number of hours represents the third quartile?
Good news – the PHStat2 program will perform all four of these calculations for us once we have entered a few basic
parameters!!
1. Open a new Excel Workbook, click on the Add-Ins tab and then click PHStat2 in the Add-Ins ribbon. Click on
Probability & Prob. Distributions and then on Normal… .
2. The Normal Probability Distribution dialog box should appear on the screen. We need to enter the mean and
standard deviation of our data set in the first two fields. After that, we have four Input Options available.
Probability for: X <=
will return P( X <= a )
Probability for: X >
will return P( X > a )
Probability for range: will return P( a <= X <= b )
X for Cumulative Percentage: will return the x-value that corresponds to the cumulative percentage we enter.
For example, if we enter 80, the program will return the 80th percentile of the data set.
We have the option of entering a Title for our output at this point. If we opt not to, we can always add a title to
our output later.
3. Enter the mean and standard deviation of the data and then enter the values that correspond to what we would
like to find.
Click the Ok button and then we will see something like this in a new worksheet:
At the top of the worksheet, we should see the mean and standard deviation we entered. Below that, all the other
information we wanted is provided.
Probability for X <=
X Value
5
Z Value
-2
P(X<=5)
0.0227501
The last entry in this table tells us P( X < = 5 ) is 0.0227501. If we relate this back to the original problem, it means there
is a 2.3% chance that the randomly selected participant spends less than 5 hours per week on their home computer.
Probability for a Range
From X Value
5.5
To X Value
9.5
Z Value for 5.5
-1.5
Z Value for 9.5
2.5
P(X<=5.5)
0.0668
P(X<=9.5)
0.9938
P(5.5<=X<=9.5)
0.9270
The last entry tells us P( 5.5 <= X <= 9.5) is 0.9270. In other words, there is a 92.7% chance that the randomly selected
participant spends between 5.5 and 9.5 hours per week on their home computer.
Probability for X >
X Value
10
Z Value
3
P(X>10)
0.0013
This table tells us there is a 0.1% chance that the randomly selected participant spends more than 10 hours per week on
their home computer.
Find X and Z Given Cum. Pctage.
Cumulative Percentage
75.00%
Z Value
0.67449
X Value
7.67449
We wanted the number of hours that represents the third quartile. According to this table, that value is approximately
7.7. In other words, 75% of all the participants spend no more than 7.7 hours per week on their home computer.
Probability for X<5 or X >10
P(X<5 or X >10)
0.0241
This table is not necessary for our problem – it is automatically generated whenever we ask the PHStat2 program to
calculate P( X > a ) and P( X <= b ) in the same dialog box. It tells us there is a 2.4% chance that the randomly selected
participant spends less than 5 hours or more than 10 hours per week on their home computer.