Download document

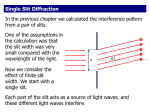
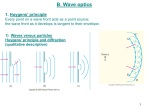
Interference and Diffraction
Chapters 36 & 37
Combination of Waves
In general, when we combine two waves to form a composite wave,
the composite wave is the algebraic sum of the two original waves,
point by point in space [Superposition Principle].
When we add the two waves we need to take into account their:
Direction
Amplitude
Phase
+
=
Combination of Waves
The combining of two waves to form a composite wave is called:
Interference
+
(Waves almost in phase)
=
Constructive interference
The interference is constructive
if the waves reinforce each other.
Combination of Waves
The combining of two waves to form a composite wave is called:
Interference
(Waves almost cancel.)
+
=
Destructive interference
(Close to p out of phase)
The interference is destructive
if the waves tend to cancel each other.
Interference of Waves
=
+
Constructive interference
(In phase)
+
=
(Waves cancel)
( p out of phase)
Destructive interference
Interference of Waves
When light waves travel different paths,
and are then recombined, they interfere.
1
Each wave has an electric field
whose amplitude goes like:
E(s,t) = E0 sin(ks-t) î
*2
Here s measures the distance
traveled along each wave’s path.
Mirror
+
=
Constructive interference results when light paths differ
by an integer multiple of the wavelength: s = m 
Interference of Waves
When light waves travel different paths,
and are then recombined, they interfere.
1
Each wave has an electric field
whose amplitude goes like:
E(s,t) = E0 sin(ks-t) î
*2
Here s measures the distance
traveled along each wave’s path.
Mirror
+
=
Destructive interference results when light paths differ
by an odd multiple of a half wavelength: s = (2m+1) /2
Interference of Waves
Coherence: Most light will only have interference for small
optical path differences (a few wavelengths), because the
phase is not well defined over a long distance. That’s
because most light comes in many short bursts strung
together.
Incoherent light: (light bulb)
random phase “jumps”
Interference of Waves
Coherence: Most light will only have interference for small
optical path differences (a few wavelengths), because the
phase is not well defined over a long distance. That’s
because most light comes in many short bursts strung
together.
Incoherent light: (light bulb)
random phase “jumps”
Laser light is an exception:
Coherent Light: (laser)
Thin Film Interference
We have all seen the effect of colored reflections
from thin oil films, or from soap bubbles.
Film; e.g. oil on water
Thin Film Interference
We have all seen the effect of colored reflections
from thin oil films, or from soap bubbles.
Rays reflected off the lower
surface travel a longer
optical path than rays
reflected off upper surface.
Film; e.g. oil on water
Thin Film Interference
We have all seen the effect of colored reflections
from thin oil films, or from soap bubbles.
Rays reflected off the lower
surface travel a longer
optical path than rays
reflected off upper surface.
Film; e.g. oil on water
If the optical paths differ by
a multiple of , the reflected
waves add.
If the paths cause a phase
difference p, reflected waves
cancel out.
Thin Film Interference
Ray 1 has a phase change of p upon reflection (1<n)
Ray 2 travels an extra distance 2t (normal incidence approximation)
1
t
2
n=1
n>1
oil on water
optical film on glass
soap bubble
Constructive interference: rays 1 and 2 are in phase
 2 t = (m+1/2)n  2 n t = (m + 1/2)  [n = /n]
Destructive interference: rays 1 and 2 are p out of phase
 2 t = m n  2 n t = m 
Thin Film Interference
When ray 2 is in phase with ray 1, they add up constructively
and we see a bright region.
Different wavelengths will tend to add constructively at
different angles, and we see bands of different colors.
1
t
2
n=1
n>1
oil on water
optical film on glass
soap bubble
Thin films work with even low
coherence light, as paths are short
When ray 2 is p out of phase, the rays interfere destructively.
This is how anti-reflection coatings work.
Diffraction
What happens when a planar wavefront of
light interacts with an aperture?
If the aperture is large
compared to the wavelength you
would expect this....
…Light propagating
in a straight path.
Diffraction
If the aperture is small
compared to the wavelength
would you expect this?
Not really…
Diffraction
If the aperture is small compared to the wavelength,
would you expect the same straight propagation? … Not really
In fact, what happens
is that: a spherical
wave propagates out
from the aperture.
All waves behave
this way.
This phenomenon of light spreading in a broad pattern,
instead of following a straight path, is called: DIFFRACTION
Diffraction
I
Slit width a:
q
Angular Spread: q ~ /a
(Actual
intensity
distribution)
Huygen’s Principle
Huygen first explained this in 1678 by proposing that all planar
wavefronts are made up of lots of spherical wavefronts..
Huygen’s Principle
Huygen first explained this in 1678 by proposing that all planar
wavefronts are made up of lots of spherical wavefronts..
That is, you see how light propagates
by breaking a wavefront into little
bits
Huygen’s Principle
Huygen first explained this in 1678 by proposing that all planar
wavefronts are made up of lots of spherical wavefronts..
That is, you see how light propagates
by breaking a wavefront into little
bits, and then draw a spherical wave
emanating outward from each little
bit.
Huygen’s Principle
Huygen first explained this in 1678 by proposing that all planar
wavefronts are made up of lots of spherical wavefronts..
That is, you see how light propagates
by breaking a wavefront into little
bits, and then draw a spherical wave
emanating outward from each little
bit. You then can find the leading edge
a little later simply by summing all
these little “wavelets”
Huygen’s Principle
Huygen first explained this in 1678 by proposing that all planar
wavefronts are made up of lots of spherical wavefronts..
That is, you see how light propagates
by breaking a wavefront into little
bits, and then draw a spherical wave
emanating outward from each little
bit. You then can find the leading edge
a little later simply by summing all
these little “wavelets”
It is possible to explain reflection and
refraction this way too.
Diffraction at Edges
what happens to the
shape of the field at this
point?
Diffraction at Edges
Light gets diffracted at the edge of an opaque barrier
 there is light in the region obstructed by the barrier
I
As The Wave Propagates Out
Spherically Its Intensity Decreases
.....this happens with an edge too..
Diffraction places a finite limit on
the formation of images
Double-Slit Interference
Because they
spread, these
waves will
eventually
interfere with
one another and
produce
interference
fringes
Double-Slit Interference
Double-Slit Interference
Double-Slit Interference
Double-Slit Interference
Bright
fringes
Double-Slit Interference
screen
Bright
fringes
Double-Slit Interference
screen
Bright
fringes
Thomas Young (1802) used double-slit
interference to prove the wave nature of light.
Double-Slit Interference
Light from the two slits travels different distances to the screen.
The difference r1 - r2 is very nearly d sinq. When the path
difference is a multiple of the wavelength these add constructively,
and when it’s a half-multiple they cancel.
P
r1
r2
d
q
L
y
Double-Slit Interference
Light from the two slits travels different distances to the screen.
The difference r1 - r2 is very nearly d sinq. When the path
difference is a multiple of the wavelength these add constructively,
and when it’s a half-multiple they cancel.
d sin q = m 
P
r1
r2
d
q
L
y
bright fringes
d sin q = ( m+1/2)  dark fringes
Double-Slit Interference
Light from the two slits travels different distances to the screen.
The difference r1 - r2 is very nearly d sin q. When the path
difference is a multiple of the wavelength these add constructively,
and when it’s a half-multiple they cancel.
P
d sin q = m 
bright fringes
d sin q = ( m+1/2)  dark fringes
r1
r2
d
y
Now use y = L tan q; and for
small y  sin q  tan q = y / L
y bright = mL/d
q
L
y dark = (m+ 1/2)L/d
Intensity in Double Slit Interference Pattern
P
The electric field at P is E = E1 + E2
r1
y
r2
d
E = EP sin (t) + EP sin (t + )
E = EP [sin (t) + sin (t + )]
q
L
This expression can be transformed using:
sin  + sin  = 2 [sin ( + ) / 2] [cos ( - ) / 2]
with  = t and  = t + 
E = 2 Ep cos ( /2) sin (t +  /2)
Intensity in Double Slit Interference Pattern
P
The electric field at P is E = E1 + E2
r1
y
r2
d
E = 2 Ep cos ( /2) sin (t +  /2)
q
L
Path difference is d sin q   / 2p = d sin q /  
  2p
E = 2 EP cos [p d sin q / ] sin (t +  /2)
d sin q

Intensity in Double Slit Interference Pattern
P
r1
y
r2
d
q
L
The electric field at P is E = E1 + E2
E = 2 EP cos [p d sin q / ] sin (t +  /2)
E = EP* sin (t +  /2)
with EP* = 2 EP cos [p d sin q / ]
The average intensity <S> is derived from
the Poynting vector S = (E x B) / 0
<S> = EP BP / 0  (EP*)2 / 2 0 c
Intensity in Double Slit Interference Pattern
P
r1
y
r2
d
The electric field at P is E = E1 + E2
E = EP* sin (t +  /2)
with EP* = 2 EP cos [p d sin q / ]
q
L

The average intensity at P is
<S> = (EP*)2 / 2 0 c
pd sin q
 E  2EP sin( t  ) cos(
)
2

[2E P cos(pd sin q / )]2
2 p dsin q
S
 4S0 cos (
)
2 c0

2 pd
S  4S0 cos ( y)
L
Intensity in Double Slit Interference Pattern
P
r1
y
r2
d
q
L
E  E1  E2  EP [sin  t  sin( t   )]


E  2EP sin( t  ) cos( )
2
2
Phase is k(r1-r2):

  2p
d sin q

pd sin q
 E  2EP sin( t  ) cos(
)
2

[2E P cos(pd sin q / )]2
2 p dsin q
S
 4S0 cos (
)
2 c0

2 pd
S  4S0 cos ( y)
L
Example: Double Slit Interference
Light of wavelength  = 500 nm is incident on a double
slit spaced by d = 50 m. What is the fringe spacing on
the screen, 50 cm away?
d
50 cm
Example: Double Slit Interference
Light of wavelength  = 500 nm is incident on a double
slit spaced by d = 50 m. What is the fringe spacing on
the screen, 50 cm away?
d
50 cm
y  L / d
 50  10 m500  10 m 50  10 m
2
 5mm
9
6
Multiple Slit Interference
With more than two slits, things get a little more complicated
P
y
d
L
Multiple Slit Interference
With more than two slits, things get a little more complicated
P
y
Now to get a bright
fringe, many paths
must all be in phase.
The brightest fringes
become narrower but
brighter;
d
L
and extra lines show up
between them.
Multiple Slit Interference
With more than two slits, things get a little more complicated
P
y
Now to get a bright
fringe, many paths
must all be in phase.
The brightest fringes
become narrower but
brighter;
d
L
and extra lines show up
between them.
Such an array of slits is called a “Diffraction Grating”
Multiple Slit Interference
All of the lines show up at the set of angles given by:
d sinq = (m/N) 
(N = number of slits). Most of these are not too bright.
The very bright ones are for m a multiple of N.
We won’t worry about the math here, just look at the
general form:
S
q
Single Slit Diffraction
Each point in the slit acts as a source of spherical wavelets
Slit width a
q
For a particular direction q, wavelets will
interfere, either constructively or destructively,
resulting in the intensity distribution shown.
Angular Spread: q ~  / a
Intensity
distribution
I
Single Slit Diffraction
Each point in the slit acts as a source of spherical wavelets
For a particular direction q, wavelets will interfere, either
constructively or destructively.
I
Result:
 sin( pa sinq )


Sq  So 
 pa sinq 
 

2
This is for a slight
of width a.
This gives
the angular
spread ~ /a.
Example: Single Slit Diffraction
Light of wavelength  =
500 nm is incident on a
slit a=50 m wide. How
wide is the intensity
distribution on the
screen, 50 cm away?
a
50 cm
Example: Single Slit Diffraction
Light of wavelength  =
500 nm is incident on a
slit a=50 m wide. How
wide is the intensity
distribution on the
screen, 50 cm away?
a
50 cm
q   / a
y  L q  50  10 m500  10 m 50  10 m  5mm
2
9
6
Example: Single Slit Diffraction
Light of wavelength  =
500 nm is incident on a
slit a=50 m wide. How
wide is the intensity
distribution on the
screen, 50 cm away?
a
50 cm
q   / a
y  L q  50  10 m500  10 m 50  10 m  5mm
2
9
What happens if the slit width is doubled?
6
Example: Single Slit Diffraction
Light of wavelength  =
500 nm is incident on a
slit a=50 m wide. How
wide is the intensity
distribution on the
screen, 50 cm away?
a
50 cm
q   / a
y  L q  50  10 m500  10 m 50  10 m  5mm
2
9
What happens if the slit width is doubled?
The spread gets cut in half.
6
The Diffraction Limit
Diffraction imposes a fundamental limit
on the resolution of optical systems:
Suppose we want to image 2 distant points,
S1 and S2, through an aperture of width a:
Two points are resolved when
the maximum of one is at
the minimum of the second
The minima occurs for
L
sin q =  / a
S1
a = slit width
S2
Using sin q  q  qmin =  / a
q
Dmin / L   / a
D
The Diffraction Limit
Diffraction therefore imposes a fundamental limit on the
resolution of optical systems:
Suppose we want to image 2 distant points, S1 and
S2 through an aperture of width a:
The image separation
is D ~ Lsinq ~ Lq.
The image blur is
B ~ L/a
L
S1
q
D
S2
To resolve individual points, we
want: separation > blur so q > /a
B