* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Light - PhysicsDCS
Atmospheric optics wikipedia , lookup
Depth of field wikipedia , lookup
Image intensifier wikipedia , lookup
Ray tracing (graphics) wikipedia , lookup
Night vision device wikipedia , lookup
Schneider Kreuznach wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Optical telescope wikipedia , lookup
Nonimaging optics wikipedia , lookup
Lens (optics) wikipedia , lookup
Retroreflector wikipedia , lookup
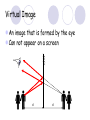
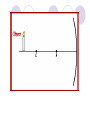
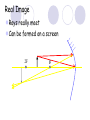
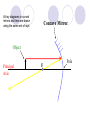
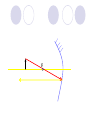
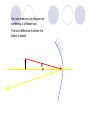
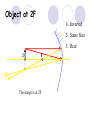
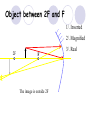
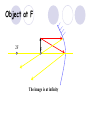
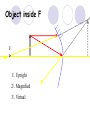
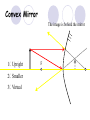
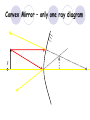
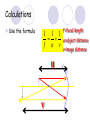
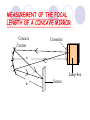
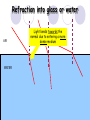
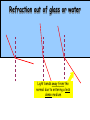
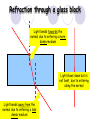
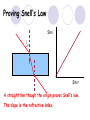
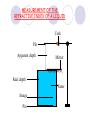
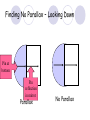
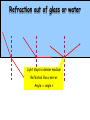
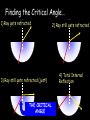
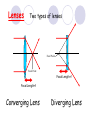
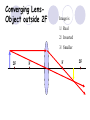
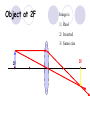
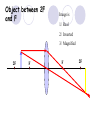
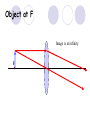
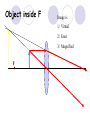
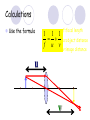
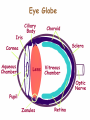
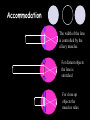
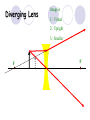
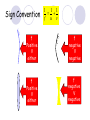
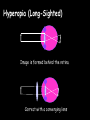
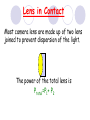
Light By Neil Bronks Light is a form of energy Crooke’s Radiometer proves light has energy Turns in sunlight as the light heats the black side Light travels in straight lines Reflection-Light bouncing off object Angle of incidenceNormal = Angle of reflection Reflected ray Incident ray Angle of incidence Angle of reflection Mirror Laws of Reflection The angle of incidence ,i, is always equal to the angle of reflection, r. The incident ray, reflected ray and the normal all lie on the same plane. Virtual Image An image that is formed by the eye Can not appear on a screen d d Real Image Rays really meet Can be formed on a screen 2F F All ray diagrams in curved mirrors and lens are drawn using the same set of rays. Concave Mirror Object Principal Axis F Pole F You can draw any ray diagram by combining 2 of these rays The only difference is where the object is based. F Ray Diagrams- Object outside 2F 1/. Inverted 2/. Smaller 2F F 3/. Real The images can be formed on a screen so they are real. Object at 2F 1/. Inverted 2/. Same Size 3/. Real 2F F The image is at 2F Object between 2F and F 1/. Inverted 2/. Magnified 2F F The image is outside 2F 3/. Real Object at F 2F F The image is at infinity Object inside F F 1/. Upright 2/. Magnified 3/. Virtual The image is behind the mirror Convex Mirror The image is behind the mirror 1/. Upright 2/. Smaller 3/. Virtual F Convex Mirror – only one ray diagram F The image is behind the mirror Uses of curved mirrors Concave Mirrors Dentists Mirrors Make –up mirrors •Convex Mirror Security Mirrors Rear view mirrors Calculations Use the formula 1 1 1 f u v u F v f=focal length u=object distance v=image distance Example An object is placed 20cm from a concave mirror of focal length 10cm find the position of the image formed. What is the nature of the image? Collect info f=10 and u=20 Using the formula 1 1 1 10 f 20 u v 1 1 1 f u v 1 1 1 v 10 20 1 1 V=20cm real v 20 Magnification What is the magnification in the last question? Well u=20 and v=20 As v 20 v m m u 20 u m 2v 2u • m=1 • Image is same size Example An object is placed 20cm from a concave mirror of focal length 30cm find the position of the image formed. What is the nature of the image? Collect info f=30 and u=20 Using the formula 1 1 1 f u v 1 1 1 1 1 1 1 30 20 v v 30 20 60 V=60cm Virtual Example An object is placed 30cm from a convex mirror of focal length 20cm find the position of the image formed. What is the nature of the image? Collect info f=-20 and u=30 Using the formula 1 1 1 20 30 v 1 1 1 f u v V=60/5cm =12cm The minus is Virtual Because the 1Mirror1is 1 5 convex v 30 20 60 Questions An object 2cm high is placed 40cm in front of a concave mirror of focal length 10cm find the image position and height. An image in a concave mirror focal length 25cm is 10cm high if the object is 2cm high find the distance the object is from the mirror. MEASUREMENT OF THE FOCAL LENGTH OF A CONCAVE MIRROR Concave mirror Crosswire u Lamp-box Screen Approximate focal length by focusing image of window onto sheet of paper. Place the lamp-box well outside the approximate focal length Move the screen until a clear inverted image of the crosswire is obtained. Measure the distance u from the crosswire to the mirror, using the metre stick. Measure the distance v from the screen to the mirror. Repeat this procedure for different values of u. Calculate f each time and then find an average value. Precautions The largest errors are in measuring with the meter rule and finding the exact position of the sharpest image. Refraction The fisherman sees the fish and tries to spear it Fisherman use a trident as light is bent at the surface Refraction into glass or water AIR WATER Light bends towards the normal due to entering a more dense medium Refraction out of glass or water Light bends away from the normal due to entering a less dense medium Refraction through a glass block Light bends towards the normal due to entering a more dense medium Light slows down but is not bent, due to entering along the normal Light bends away from the normal due to entering a less dense medium Laws of REFRACTION The incident ray, refracted ray and normal all lie on the same plane SNELLS LAW the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant for 2 given media. sin i = n (Refractive Index) sin r Proving Snell’s Law Sin i i r Sin r A straight line though the origin proves Snell’s law. The slope is the refractive index. Proving Snell’s Law Sin i i Glass Block Protractor r Sin r A straight line though the origin proves Snell’s law. The slope is the refractive index. H/W LC Ord 2006 Q2 Refractive Index Ratio of speeds cair 300000000m / s n 1.5 cwater 200000000m / s Real and Apparent Depth A pool appears shallower Re al n Apparent MEASUREMENT OF THE REFRACTIVE INDEX OF A LIQUID Cork Pin Apparent depth Mirror Real depth Water Image Pin Finding No Parallax – Looking Down Pin at bottom Pin reflection in mirror Parallax No Parallax Set up the apparatus as shown. Adjust the height of the pin in the cork above the mirror until there is no parallax between its image in the mirror and the image of the pin in the water. Measure the distance from the pin in the cork to the back of the mirror – this is the apparent depth. Measure the depth of the container – this is the real depth. Calculate the refractive index n= Real/Apparent Repeat using different size containers and get an average value for n. Refraction out of glass or water Light stays in denser medium Reflected like a mirror Angle i = angle r Snell’s Window Finding the Critical Angle… 1) Ray gets refracted 3) Ray still gets refracted (just!) THE CRITICAL ANGLE 2) Ray still gets refracted 4) Total Internal Reflection Semi-Circular Block Expt and on the internet click here Mirages Critical Angle Varies according to refractive index 1 sin C n 1 sin 45 n 1 0.7071 n 1 n 0.7071 n 1.41 Uses of Total Internal Reflection Optical fibres: An optical fibre is a long, thin, transparent rod made of glass or plastic. Light is internally reflected from one end to the other, making it possible to send large chunks of information Optical fibres can be used for communications by sending e-m signals through the cable. The main advantage of this is a reduced signal loss. Also no magnetic interference. Practical Fibre Optics It is important to coat the strand in a material of low n. This increases Total Internal Reflection The light can not leak into the next strand. 1) Endoscopes (a medical device used to see inside the body): 2) Binoculars and periscopes (using “reflecting prisms”) Now is a good time to get out the light demo kit H/W LC Ord 2003 Q7 Lenses Two types of lenses Focal Point Focal Point Focal Length=f Focal Length=f Converging Lens Diverging Lens Ray Diagrams Optical Centre F F 2F F F 2F Converging LensObject outside 2F Image is 1/. Real 2/. Inverted 3/. Smaller 2F F F 2F Object at 2F Image is 1/. Real 2/. Inverted 3/. Same size 2F F F 2F Object between 2F and F Image is 1/. Real 2/. Inverted 3/. Magnified 2F F F 2F Object at F Image is at infinity F F Object inside F Image is 1/. Virtual 2/. Erect 3/. Magnified F F H/W Draw the 5 ray diagrams for the converging lens and the diagram for the diverging lens . Write 3 characteristics of each image. Calculations Use the formula 1 1 1 f u v f=focal length u=object distance v=image distance u 2 F F F v 2F Example An object is placed 30cm from a converging lens of focal length 40cm find the position of the image formed. What is the nature of the image? Collect info f=40 and u=30 Using the formula 1 1 1 40 f 30 u v 1 1 1 f u v 1 11 11 1 - = vu -120 v vf fu40 30 V=120cm virtual Magnification What is the magnification in the last question? Well u=30 and v=120 As 120 v v mm 30 u u m 4v 1u • Image is larger MEASUREMENT OF THE FOCAL LENGTH OF A CONVERGING LENS Show on OPTICAL BENCH Lamp-box with crosswire Screen Lens u v 1. Place the lamp-box well outside the approximate focal length 2. Move the screen until a clear inverted image of the crosswire is obtained. 3. Measure the distance u from the crosswire to the lens, using the metre stick. 4. Measure the distance v from the screen to the lens. 5. Calculate the focal length of the lens using 1 1 1 f u v 6. Repeat this procedure for different values of u. 7. Calculate f each time and then find the average value. H/W LC Ord 2002 Q3 Accommodation The width of the lens is controlled by the ciliary muscles. For distant objects the lens is stretched. For close up objects the muscles relax. Diverging Lens Image is 1/. Virtual 2/. Upright 3/. Smaller F F Example An object is placed 30cm from a diverging lens of focal length 20cm find the position of the image formed. What is the nature of the image? Collect info f=-20 and u=30 Using the formula 1 1 1 20 30 v 1 1 1 f u v V=60/5cm =12cm The minus is Virtual Because the 1 1 1 5 Diverging lens v 30 20 60 Example An object is placed 30cm from a diverging lens of focal length 60cm find the position of the image formed. What is the nature of the image? (Remember f must be negative) Collect info f=-60 and u=30 Using the formula 1 1 1 -60 30 f u v 1 1 1 f u v 1 11 11 1 - = -60 uf 30vu -20v vf V=20cm virtual Magnification What is the magnification in the last question? Well u=30 and v=20 As v 20 v m m u 30 u m 2v 3u • Image is smaller Sign Convention 1 1 1 f u v f Positive V either f negative V negative f Positive V either f negative V negative Myopia (Short Sighted) Image is formed in front of the retina. Correct with diverging lens. Hyperopia (Long-Sighted) Image is formed behind the retina. Correct with a converging lens Power of Lens Opticians use power to describe lenses. 1 P= f So a focal length of 10cm= 0.1m is written as P=10m-1 A diverging lens with a negative focal length f=-40cm=-0.4m Has a power of P = -2.5m-1 Lens in Contact Most camera lens are made up of two lens joined to prevent dispersion of the light. The power of the total lens is Ptotal=P1+ P2 H/W LC Higher 2002 Q12 (b) LC Higher 2003 Q3