Download Lecture_1

MSE 630
Introduction to Solid State Physics
Topics:
Structure of Crystals
classification of lattices
reciprocal lattices
bonding in crystals
Vibrations and Waves in Crystals - Phonons
Electrons in Crystals
free electrons in metals
electrons in periodic potentials
semiconductors
•Conductivity?
•Types?
•Metals, Semiconductors, Insulators, and Superconductors
•Atoms and Electrons
•Electronic Structure of materials
•The Bohr Model
•Quantum Mechanics
– Schrodinger Wave Eqn
– Atomic structure and Periodic Table
– Bonding forces in materials
Ionic Bond – electron transfer and electrostatic attraction
Non directional
Covalent Bond: electron sharing for stable outer shells
Highly directional
Metallic bond: electron sharing between charged ion cores
Non directional
The bond type influences the mechanical properties
Both ionic and metallic bonds
form close packed structures.
Ions, though, have to maintain
charge neutrality, so any
deformation in ionic solids must
be large enough to move the
atoms back into registry. Metals
do not have this restriction.
Hence, ionic solids are brittle,
while metals are ductile.
Other, weaker bonds
Hydrogen bond: hydrogen
acts as infinitesimal cation
attracting two anions
van der Waals bond: weak
attraction between molecular
dipoles
The structure of an ionic
compound depends upon the
ratio of the cation to the anion
The crystal lattice
A point lattice is made up of regular,
repeating points in space. An atom or
group of atoms are tied to each lattice
point
14 different point lattices,
called Bravais lattices,
make up the crystal
system. The lengths of the
sides, a, b, and c, and the
angles between them can
vary for a particular unit
cell.
Three simple lattices that describe metals are Face Centered Cubic (FCC)
Body Centered Cubic (BCC) and Hexagonal Close Packed (HCP)
Whether a close packed crystal is FCC or HCP depends upon the stacking
sequence of close packed planes
Diamond, BeO and GaAs are examples of FCC structures with two atoms per
lattice point
Polymers are made up of repeating units “mers”, that make up a long chain.
The chain may be cross-linked, or held together with van der Waals or
hydrogen bonds
Structures may be crystalline, having repeating structure, or
amorphous, having local structure but no long-range structure
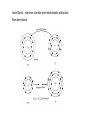
Directions in a crystal lattice – Miller Indices
Vectors described by multiples of
lattice constants: ua+vb+wc
e.g., the vector in the illustration
crosses the edges of the unit cell
at u=1, v=1, c=1/2
Arrange these in brackets, and
clear the fractions:
[1 1 ½] = [2 2 1]
Negative directions have a
bar over the number
_
e.g.,
1  1
Families of
crystallographically
equivalent directions, e.g.,
[100], [010], [001] are
written as <uvw>, or, in
this example, <100>
Directions in HCP crystals
a1, a2 and a3 axes are 120o apart, z axis is
perpendicular to the a1,a2,a3 basal plane
Directions in this crystal system are
derived by converting the [u′v′w′] directions
to [uvtw] using the following convention:
[u ' v' w' ]  [uvtw]
n
u  (2u 'v' )
3
n
v  (2v'u ' )
3
t  (u 'v' )
w  nw'
n is a factor that reduces
[uvtw] to smallest integers.
For example, if
u′=1, v′=-1, w′=0, then
_
[uvtw]= [11 00]
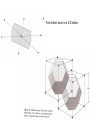
Crystallographic Planes
To find crystallographic planes are
represented by (hkl). Identify
where the plane intersects the a, b
and c axes; in this case, a=1/2,
b=1, c=∞
Write the reciprocals 1/a, 1/b, 1/c:
1
1
2
1
k
1
1
l

h
Clear fractions, and put into
parentheses:
(hkl)=(210)
If the plane interesects
the origin, simply
translate the origin to an
equivalent location.
Families of equivalent
planes are denoted by
braces:
e.g., the (100), (010),
(001), etc. planes are
denoted {100}
Planes in HCP crystals are
numbered in the same way
e.g., the plane on the left intersects
a1=1, a2=0, a3=-1,_ and z=1, thus
the plane is (10 11)
METALLIC CRYSTALS
• tend to be densely packed.
• have several reasons for dense packing:
-Typically, only one element is present, so all atomic
radii are the same.
-Metallic bonding is not directional.
-Nearest neighbor distances tend to be small in
order to lower bond energy.
• have the simplest crystal structures.
We will look at three such structures...
3
THEORETICAL DENSITY, 
Example: Copper
Data from Table inside front cover of Callister (see next slide):
• crystal structure = FCC: 4 atoms/unit cell
• atomic weight = 63.55 g/mol (1 amu = 1 g/mol)
• atomic radius R = 0.128 nm (1 nm = 10 -7cm)
Result: theoretical Cu = 8.89 g/cm3
Compare to actual: Cu = 8.94 g/cm3
11
IONIC BONDING & STRUCTURE
• Charge Neutrality:
--Net charge in the
structure should
be zero.
--General form:
• Stable structures:
--maximize the # of nearest oppositely charged neighbors.
15
COORDINATION # AND IONIC RADII
• Coordination # increases with
Issue: How many anions can you
arrange around a cation?
16
The Reciprocal Lattice and Waves in
Crystals
We use the reciprocal lattice to calculate
wave behavior in crystals because sound,
optical and electrical properties pass
through the crystal as waves
Because crystals are periodic, properties
throughout the crystal will be the same as
those surrounding any lattice point,
contained in a volume known as a “Brillion
Zone”
X-ray diffraction and crystal structure
•
•
X-rays have a wave length, l0.110Å.
This is on the size scale of the structures
we wish to study
X-rays interfere
constructively when the
interplanar spacing is
related to an integer
number of wavelengths in
accordance with Bragg’s
law:
nl  2d sin 
Because of the numbering system,
atomic planes are perpendicular to
their corresponding vector,
e.g., (111) is perpendicular to [111]
The interplanar spacing for a cubic
crystal is:
d hkl 
a
h2  k 2  l 2
Because the intensity of the
diffracted beam varies depending
upon the diffraction angle, knowing
the angle and using Bragg’s law
we can obtain the crystal structure
and lattice parameter
The Reciprocal Lattice
To analyze the atomic structure and resulting
properties of crystals, we introduce the concept
of the “reciprocal lattice”
A reciprocal lattice vector is defined as
G = n1b1 + n2b2 + n3b3
Where n1, n2, n3 are integers and b1, b2 and b3 are
primitive vectors in the reciprocal lattice
Why do we need reciprocal space?
Because waves or
n(r )   nG exp( iG  r )
vibrations can be made
up of a series of waves of or
n(r )   ng cos(G  r )  i sin( G  r ) 
other frequencies, i.e.,
expressed as a Fourier
Series:
We want G∙r to equal 2p
at boundaries. Therefore
2p
b
a
or
bi  a j  2pij
Wave reflection in reciprocal space
The reciprocal lattice vector, G = Dk
Calculating the reciprocal lattice
We construct the axis
vectors b1, b2 and b3
of the reciprocal
lattice using the
following formulas:
a2  a3
b1  2p
a1  (a2  a3 )
a3  a1
b2  2p
a1  (a2  a3 )
a1  a2
b3  2p
a1  (a2  a3 )
First brillion zone in a 2-D lattice
BCC primitive lattice vectors:
1
axˆ  yˆ  zˆ 
2
1
a2  a xˆ  yˆ  zˆ 
2
1
a 3  axˆ  yˆ  zˆ 
2
a1 
FCC primitive lattice vectors:
1
axˆ  yˆ 
2
1
a2  a yˆ  zˆ 
2
1
a 3  azˆ  xˆ 
2
a1 
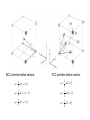
Brillion Zones
BCC Brillion Zone
FCC Brillion Zone
Brillion Zones are the same as Wigner-Seitz cells
in reciprocal space