Download Hour Exam 3

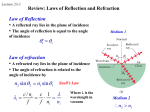
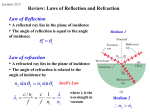
Polarization
Properties of
Light / EM waves
Why is that?
In many cases light is radiated/scattered by
oscillating electric dipoles.
Maximum intensity
+
Intensity lobe
–
Less intensity
No radiation along direction of motion!
Geometric Optics
• So far EM waves in vacuum
• What happens to EM waves (usually light) in different
materials?
• Restriction: waves whose wavelength is much shorter than the
objects with which it interacts.
• Pretend that light propagates in straight lines, called rays.
• Our primary focus will be on the REFLECTION and
REFRACTION of these rays at the interface of two materials.
incident
ray
reflected
ray
MATERIAL 1
MATERIAL 2
refracted
ray
Reflections…
How does light interact with matter?
A simple description
•
“Charge on spring” description of electrons ‘bound’ to atoms
in materials
•
Light interacts with matter by causing internal charges in the
material to oscillate
light frequency

•
o
“natural” or
“resonant” frequency
of charge on spring
Due to inertia, “bound” charges in a material respond
sluggishly to incident light
driven charges re-emit waves that are out of phase with incident wave
Back to capacitors!
• Capacitor with vacuum
between plates
• Capacitor with dielectric
between plates
– magnitude of E-field is
reduced by “relative
dielectric constant”
• Why?
– dielectric polarization…...

E
0

E
 0
+
+
+
+
+
+
+
+
vacuum
-
-
-
-
-
-
-
-
+
+
+
+
+
+
+
+
-
-
dielectric
-
-
-
-
-
-
relative dielectric
constant can be large
Index of Refraction
• The wave incident on an interface can not only reflect, but it
can also propagate into the second material.
• The speed of an electromagnetic wave is different in matter
than it is in vacuum.
• from Maxwell’s eqns in vacuum:
c
1
m 0 0
• How are Maxwell’s eqns in matter different?
0≡0
v
m0  m ≈ m0 (for most materials)
1
m

1
m0  0

c

• Therefore, the speed of light in matter is related to the speed of
light in vacuum by:
c
v
n
where n = “index of refraction” of the material:
n   1
The index of refraction is frequency dependent:
For example, in glass
nblue = 1.53
nred = 1.52
Refraction
• How is the angle of refraction related to the
angle of incidence?
– Unlike reflection, q 1 cannot equal q 2 !!
» Why??
q1
n1
n2
Remember v = fl
» n1  n2  v1  v2
but the frequencies (f1, f2) must be the same
 the wavelengths must be different!
Therefore, q 2 must be different from q 1 !!
q2
l1 v1 n2


l2 v2 n1
Snell’s Law
• From the last slide:
l1 v1 n2


l2 v2 n1
q2
q1 L
q2
q1
q1
q2
q2
n1
n2
Huygen’s
Principle
The two triangles above each have hypotenuse L
l2
l1

\ L
sin q 2 sin q1
But,
l1
v
n
 1  2
l2 v2
n1
l1 sin q1

l2 sin q 2
n1 sin q1  n2 sin q 2
Index of refraction
Dispersion
1.54
ultraviolet
absorption
bands
1.52
1.50
frequency
white light
prism
Split into Colors
Dispersion in more detail:
Effects of wavelength dependence of n
•
Dispersion:
n depends on
wavelength!
nblue > nred
vblue < Vred
Total Internal Reflection
– Consider light moving from glass (n1=1.5) to air (n2=1.0)
n1
incident
ray
q1 qr
reflected
ray
GLASS
n2
q2
refracted
ray
AIR
sin q 2 n1
 1
sin q1 n2
q 2  q1
1
I.e., light is bent away from the normal.
as q1 gets bigger, q2 gets bigger, but q2
can never get bigger than 90° !!
In general, if sin q1 > (n2 / n1), we have NO refracted ray;
we have TOTAL INTERNAL REFLECTION.
For example, light in water which is incident on an air surface with
angle q1 > qc = sin-1(1.0/1.5) = 41.8° will be totally reflected. This
property is the basis for the optical fibers used in communication.
Examples: refraction at water/air interface
•
Diver’s illusion
97º
Diver sees all of horizon
refracted into a 97°cone
Why is the sky blue?
• Light from Sun scatters off of air particles–“Rayleigh scattering”
– Rayleigh scattering is wavelength-dependent.
– Shorter wavelengths (blue end of the visible spectrum) scatter more.
• This is also why sunsets are red!
– At sunset, the light has to travel through more of the
atmosphere.
– If longer wavelengths (red and orange) scatter less…
– The more air sunlight travels through, the redder it will
appear!
– This effect is more pronounced if there are more particles
in the atmosphere (e.g., sulfur aerosols from industrial
pollution).
Polarization of Light
http://www.walter-fendt.de/ph14e/emwave.htm
Unpolarized Light
• We have primarily been considering light that has
a definite polarization (e.g., linear or circular).
Most sources – a candle, the sun, any light bulb –
produce light that is unpolarized :
–
it does not have a definite direction of the electric field
– there is no definite phase between orthogonal
components
– the atomic or molecular dipoles that emit the light are
randomly oriented in the source
– the intensity of light transmitted through a polarizer is
always half the intensity of the unpolarized input,
regardless of the orientation of the polarizer
(though of course the output is polarized!)
These are all equivalent ways of describing the same thing.
Polarization
http://www.launc.tased.edu.au/online/sciences/physics/Polari.htm
Absorption
Polarization by absorption
Polarization by absorption
http://www.launc.tased.edu.au/online/sciences/physics/Polari.htm
http://www.colorado.edu/physics/2000/applets/lens.html
Applications
• Sunglasses
– The reflection off a
horizontal surface (e.g.,
water, the hood of a car,
etc.) is strongly polarized.
Which way?
– A perpendicular polarizer
can preferentially reduce
this glare.
Double Refraction or Birefrigence
Double Refraction or Birefrigence
Reflection
• The angle of incidence equals the angle of reflection q i =q r ,
where both angles are measured from the normal:
• Note also, that all rays lie in the “plane of incidence”.
qi qr
• Why?
» This law is quite general; we supply a limited justification
when surface is a good conductor (reasonable restriction
since reflection is dominant in this case)
First consider a wave Em  Ex cos(kz  wt ) hitting a conductor at
normal incidence:
The electrons on the surface of the metal will
experience a force F=eE → acceleration →
radiation in  ẑ.
e
Reflection
Brewster’s Law
n = sin(i)/sin(r)
= sin(i)/sin(90-i)
= tan(i)
http://micro.magnet.fsu.edu/
primer/java/polarizedlight/br
ewster/index.html
http://www.launc.tased.edu.au/online/sciences/physics/Polari.htm
L23:Polarization by Scattering
• Suppose unpolarized light encounters an atom and scatters
(energy absorbed & reradiated).
– What happens to the polarization of the scattered light?
– The scattered light is preferentially polarized perpendicular to the
plane of the scattering.
» For example, assume the incident unpolarized light is moving
in the z-direction.
» Scattered light observed along the x-direction (scattering
plane = x-z) will be polarized along the y-direction.
» Scattered light observed along the y-direction (scattering
plane = y-z) will be polarized along the x-direction.
y
This box contains atoms
which “scatter” the light
beam
x
z
Scattering
Applications
• Polarized sky
– The same argument applies to light scattered off the sky:
Which photo was taken with a polaroid?
http://www.colorado.e
du/physics/2000/apple
ts/polarized.html
http://home3.netcarrier.com/~chan/EM/PROGRAMS/POLARIZATION/
Application: LCD Display
END