Download Διαφάνεια 1

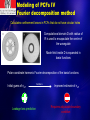
Presentation in the frame of
Photonic Crystals course
by R. Houdre
Photonic Crystal Fibers
Georgios Violakis
EPFL, Lausanne
June 2009
Outline
Introduction to Photonic Crystal Fibers
Fiber types / classification
Common Fabrication Techniques
Properties of Microstructured Optical Fibers
Properties of Photonic Bandgap Fibers
Modeling of Photonic Crystal Fibers
Applications of PCFs
Optical Fibers
An optical fiber is a glass structure specially designed in
order to efficiently guide light along its length (long distances)
Step Index Optical Fibers
Light guidance by means of total internal reflection.
Widely utilized in telecommunications
Polymer
jacket
Fiber cladding
 c  arcsin( n2 / n1 )
Fiber core
Photonic Crystal Fibers
2 main classes of PCFs
High Index core Fibers
High N.A.
Large
Mode Area
Highly
non linear
Photonic Bandgap Fibers
Low Index
Core
Hollow
Core
Bragg
Fiber
High Index Core Fibers
High Index
Fiber core
Light guidance by means of
modified total internal reflection.
Introduction of low index (e.g. air)
capillaries in the “cladding” area,
effectively reduces the refractive
index of the core surrounding area,
allowing TIR
Low index capillaries,
e.g. air channels
High index material,
e.g. silica glass
Photonic Bandgap Fibers
In most cases the core has a lower
refractive index than the cladding area
“True” photonic crystal fibers.
Light guidance by means of light trapping
in the core, due to the photonic bandgap
zones of the “cladding”
Cladding structure must
be able to exhibit at least
one photonic bandgap at
the frequency of interest
Fabrication Techniques I
a) Preparation of each capillary
b) Assembly of capillaries to the desired structure
c) Preparation of the preform
d) Fiber drawing
Fabrication Techniques II
Variations of technique depending on
the preform material
Chalcogenide fibers
Polymer fibers
Compound glass fibers
Variations of technique depending on
the fiber layout
Honeycomb structure
Hollow core fibers
etc…
Properties of Microstructured
Optical Fibers I
Optical properties affected by:
d
a) Geometry of the fiber
b) Core/cladding/defect
materials
d/Λ typically varies between a few % - 90%
Λ
Λ
typically varies between 1 – 20 μm
Core size usually between 5 – 20 μm
Core usually made of the same material as
the cladding (high quality fused silica), but
in some cases it can contain dopants
By adjusting the geometrical features of the fibers one can adjust the light
propagation properties from highly linear performance to highly non-linear
propagation
Properties of Microstructured
Optical Fibers II
In standard optical fibers the number of modes supported is calculated by:
Veff  k  a nco2  ncl2 
2

a nco2  ncl2
“Effective” refractive index of cladding is
wavelength dependant
2
Veff   k 2 nco2   fsm
As the frequency is increased, the
effective index of the cladding ncl is
approaching nco and equation Veff can
reach a stationary value, determined
by the d/Λ ratio
Endlessly Single Mode Fibers
Possibility to design a fiber with d/Λ
below a certain value, ensuring that the
Veff value does not exceed the second
order mode cutoff value over the
desired wavelength range (dashed line)
Properties of Microstructured
Optical Fibers III
Dispersion properties
Dispersion is calculated using
the full vectorial plane wave
approximation
Possible to have broadband
near zero dispersion flattened
behavior
Cladding morphology has a
great effect on dispersion
properties
Triangular hole structure
Λ = 2.3μm, various d
Larger pitch results in reduced
dispersion for fixed λ and d
Properties of Photonic Bandgap
Fibers I
Optical properties affected by:
a) Geometry of the fiber
b) Core/cladding/defect
materials
Numerical methods applied to achieve
bandgap diagram
1st forbidden frequency domain: ω/c = kz/neq
where neq: equivalent index of silica + holes and it is λ dependant
Grey area corresponds to the classical guiding in fibers by TIR for which as long as k z/neq ≥
ω/c (=kfree space) the wave propagating in the core is confined there (no refraction)
2nd forbidden frequency domain: The four narrow bands
caused by the photonic crystal structure and are associated with Bragg reflections
Properties of Photonic Bandgap
Fibers II
Core – cladding design
The cladding must exhibit photonic
bandgaps that cross the air line
(requirement for hollow core fibers)
Number of modes in the core region:
N PBG 
2
2
2
(k 2 neff
,co   L )( Deff / 2)
4
NPBG is the number of PBG-guided modes, Deff: effective core diameter for PC, βL is the
lower propagation constant of a given PBG
Core determination by the above equation for desired number of modes
Properties of Photonic Bandgap
Fibers III
Losses
Losses decrease exponentially with the number of air hole rings in the cladding
For hollow core fibers it is also crucial the shape of the core
Dispersion
And area of mode
Higher leakage for first two core geometries
d/Λ ration also important as well as the air-silica
filling ration
Theoretically predicted attenuation: 0.13dB/km at 1.9μm
Experimentally measured attenuation : 1.2dB/km at 1.62μm
Properties of Photonic Bandgap
Fibers IV
Dispersion
Λ = 1.0μm, dcl = dco = 0.40Λ
Λ = 2.3μm, dcl = 0.60Λ
Anomalous dispersion can be used for
dispersion management (dispersion
compensation in optical transmission links)
By adjusting core size and cladding
properties it is possible to achieve
broadband, near zero dispersion flattened
behavior
Properties of Photonic Bandgap
Fibers V
Special properties
By inducing “defects” in the cladding area (for example a change of size of two
of the holes in the first ring outside
the core area) it is possible to induce
birefringence in the fiber (two
polirazationstates experience different
β/k values)
Possibility to design fibers with the second order mode confined and the
fundamental leaky (mode propagation manipulation – sensing)
Simulations reveal the presence of ring
shaped resonant modes between the
core-cladding interface (issue of
ongoing research)
Modeling of PCFs I
The effective index approach I
Simple numerical tool
Evaluates the periodically repeated cladding
structure an replaces it with an neff.
Core refractive index usually same as matrix
material (e.g. fused silica)
Analogy to step index fibers and use of calculation
tools readily available
Determination of neff
Determination of cladding mode field, Ψ, by solving the scalar
wave equation within a simple cell centered on one of the holes
Approximation by a circle to facilitate calculations
Application of boundary conditions (dΨ/ds)=0
Propagation constant of resutling fundamental mode, βfsm used in:
neff 
 fsm
k
Modeling of PCFs I
The effective index approach II
neff 
 fsm
k
nco = nsilica
ncl = neff
rcore = 0.5*Λ
or
0.62*Λ
Full analogy to a step index fiber realized  Use of tools for step index fibers
Refractive index in matrix material can be also described
as being wavelength dependent using the Sellmeier
formula
Simple
Minimum computational
requirements
2
A

n2  1   2 i
i 1   Bi
Qualitative method
Cannot compute
photonic bandgaps
3
Modeling of PCFs II
Plane-wave expansion method I
First theoretical method to accurately analyze photonic crystals
Takes advantage of the
cladding periodicity:
E (r , t )  E (r )e jt
Bloch’s
E ( r )  V k ( r )e  j k r
H (r , t )  H (r )e jt
theorem
H ( r )  U k ( r )e  j k r
V and U in reciprocal space
Fourier expansion in terms of the reciprocal lattice vectors G
E (r )   E k (G )e  j ( k G )r
Fourier transformation
H (r )   H k (G )e  j ( k G )r
Maxwell’s equations
G
G
Wave equation in the
reciprocal space
Can be re-written in matrix form and solved using standard numerical routines as
eigenvalue problems
Once the wave equation has been solved for one of the fields (e.g. H)
E (r ) 
1
 H (r )
j r (r ) 0
Modeling of PCFs II
Plane-wave expansion method II
2 dimensional photonic crystals with hexagonal symmetry

( x  y 3)
2

R2  ( x  y 3)
2
R1 
2
(x  y

2
G2 
(x  y

G1 
R1, R2: real space primitive lattice vectors
G1, G2: reciprocal lattice vectors
R i  G j  2i , j
3
)
3
3
)
3
Solutions for k vectors restricted
in the 1st Brillouin zone
Calculation of the εr-1(G) which is
required to set up the matrix equation
Solution of E and H
Calculates PBGs
Good agreement
with experiments
Widely used
Unsuitable for large
structures
Unsuitable for full
PCF analysis
Modeling of PCFs III
Multipole method I
Method used to calculate confinement losses in PCFs
Similar to other expansion methods, but:
uses many expansions, one for each of
the fiber holes in the fiber cladding
Does not require periodicity
Calculation of complex
propagation constant (confinement
losses)
Around a cylinder l the longitudinal E-field component Ez is:
Ez 

(l )
e
(l )
(l )
e
[
a
J
(
k
r
)

b
H
(
k
 m m  l m m  rl )] exp(  jml ) exp(  jz )
m  
with ke  k02 ne2   2 being the transverse wave number in silica
Inside the cylinder where ni=1, Ez is:
Ez 

(l )
i
[
c
J
(
k
 m m  rl )] exp(  jml ) exp(  jz )
m  
where ki   2  k02 ni2
Application of
Boundary conditions:
am(l ) bm(l ) cm(l )
Modeling of PCFs III
Multipole method II
In order to describe leaky modes,
cladding is surrounding by jacketing
material with nj = ne-jδ, δ<<1
Without jacket, expansions lead to fields
that diverge far away from the core,
because the modes are not completely
bound
Confinement loss determined by the
multipole method. Λ = 2.3μm,
λ=1.55μm
Modeling of PCFs III
Multipole method IIΙ
Calculates confinement loss
Does not require symmetrical
boundary conditions
Does not make the assumption
that the cladding area is infinite
Computational
intensive
Cannot analyze arbitrary
cladding configurations
(applies only for circular
holes)
Modeling of PCFs IV
Fourier decomposition method
Calculates confinement losses in PCFs that do not have circular holes
Computational domain D with radius of
R is used to encapsulate the centre of
the waveguide
Mode field inside D is expanded in
basis functions
Polar-coordinate harmonic Fourier decomposition of the basis functions
Initial guess of neff
Leakage loss prediction
Iterations
Improved estimate of neff
Requires adjustable boundary
condition
Modeling of PCFs V
Finite Difference method I
Finite Difference Time Domain method
Maxwell’s equations can be
discretized in space and time
(Yee-cell technique)
Field components of the
mesh could be the discrete
form of x-component of
Maxwell’s first curl equation:
H x
1  E E y 

   z 
t
  y
z 
H
1
n
2
x i, j
H
1
n
2
x i, j
n
n


E

E
n 
z i, j
t  z i , j 1

 j E y 

i, j
i , j 
y



n: discrete time step
i,j: discretized mesh point
Δt: time increment
Δx, Δy: intervals between 2
neighboring grid points
Modeling of PCFs V
Finite Difference method II
Finite Difference Time Domain method
Boundary conditions using in most
cases the Perfeclty Matched Layer
(PML) technique
Fields in time domain
Artificial initial field distribution -> non
physical components disappear in the
time evolution and physical
components (guided modes) remain
Fourier transformation
General approach
Fields in frequency domain
Requires detailed treatment of
boundaries
Describes variety of structures
Computationally intensive
Modeling of PCFs VI
Finite Element method I
The most generally used method for various physical problems
Method has been used for the
analysis of standard step index fibers
and it was later (2000) applied for
photonic crystal fibers
Maxwell’s differential equations are solved for a set of elementary subspaces
Subspaces are considered homogenous (mesh of triangles or quadrilaterals)
Maxwell’s equations applied for each element
Boundary conditions (continuity of the field)
neff, E- and H- field can be numerically calculated
Modeling of PCFs VI
Finite Element method II
Propagation mode results indicate that modes exhibit
at least two symmetries
Introduction of Electric and Magnetic Short Circuit.
Study of ¼ of the fiber area – decrease in
computational time
Reliable (well-tested) method
Accurate modal description
Complex definition of calculation
mesh
Can become computationally
intensive
Modeling of PCFs VII
Other methods
Finite Difference Frequency Domain
General approach, well tested,
analyses any structure
Computationally very intensive, detailed
boundary conditions
Beam propagation method
Reliable method, can use complex
propagation constant
Also computationally intensive
Equivalent Averaged Index method
Simple and efficient (fast method)
Qualitative results
Modeling examples of two PCFs
ESM-12-01 Blaze photonics (Crystal Fibre A/S)
Core diameter: 12μm
Holey region diameter: 60μm
Cladding diameter: 125μm
LMA-10 Crystal Fibre A/S
Mode field calculations using the
multipole method
Calculation of the fundamental mode
using the freely available CUDOSMOF tools which are based on the
multipole method
White holes represent air holes and
blue background the silica matrix
http://www.physics.usyd.edu.au/cudos/mofsoftware/
Mode field calculations using the
FDTD method
Calculation of the
fundamental mode using
commercially available
FDTD software.
(OptiFDTD)
Higher order modes,
though calculated, are
leaky and are not
supported by the fiber
which is endlessly single
mode
http://www.optiwave.com/
Mode field calculations using the
FEM method
Calculation of the
fundamental mode using
commercially available
FEM software. (COMSOL
multiphysics)
Higher order modes were
not found to be supported
for this kind of optical fiber
http://www.comsol.com/
Photonic Crystal Fiber Applications
Light guidance for λ that silica strongly absorbs (IR range)
High power delivery
Gas-filling the core (sensing, non-linear processes)
Gas-lasers (hollow core) / Fiber lasers (doped core)
In-fibre tweezers (nanoparticle transportation in the hollow core)
Tunable sensors (liquid crystals in PCFs)
Thank you!