Download Adaptive Optics Nicholas Devaney GTC project, Instituto de

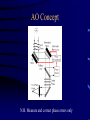
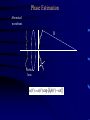
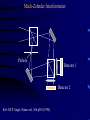
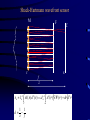
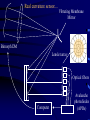
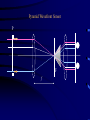
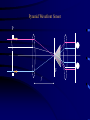
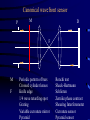
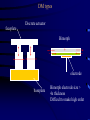
Adaptive Optics
Nicholas Devaney
GTC project, Instituto de Astrofisica de Canarias
1. Principles
2. Multi-conjugate
3. Performance & challenges
Outline
•
•
•
•
•
•
Background (reminder)
Concept of Adaptive Optics
Gain in Image quality
Components
Designing a system
Limitations
Effect of turbulence on Images
• The spatial resolution of ground based telescopes is
limited to that of an equivalent diffraction-limited
telescope of diameter r0 - the Fried parameter
• The Fried parameter is determined by the integrated
strength of turbulence along the line of sight. It
therefore depends on zenith angle ().
(airmass=1/cos().)
• Since it is defined in terms of phase (1 rad of rms
wavefront error), it also depends on wavelength

r0  0.423k (cos  )
r0  
2
6
5
1
C
2
N
(h)dh
r0  (airmass )

3
5

3 / 5
AO Concept
N.B. Measure and correct phase errors only
Modal Correction
• Can write phase error as an expansion of Zernike
polynomials (for example)
 (r )   ai Z (r )
n
• Zernikes are used mostly because everyone uses
them ! The first correspond to familiar Seidel
aberrations (tip, tilt, defocus,Astigmatism+defocus,
Coma+tilt etc.)
• Useful to consider what happens as we correct
n=1,2,3.... Zernikes; n is the order of correction.
Modal Correction
• When j terms are perfectly corrected, the residual
variance is given by
D
 j   j  
 r0 
5
3
• The  coefficients have been calculated by Noll
(JOSA 66, 207-211, 1975)
• In order to determine how image quality improves as
a function of the degree of compensation, first
consider how the phase structure function changes...
Modal Compensation
• Recall that for uncompensated turbulence the
structure function is given by
r
D (r )  6.88 
 r0 
5
3
• Cagigal & Fernandez define a Generalised Fried
parameter,0, such that for r < lc
D
D (r )  6.88 
 0 
5
3
• The Generalised Fried parameter is related to the
residual variance by
 3.44 

 0  


j


3
5
Structure function with modal compensation
Modal Compensation
• The partially corrected PSF has two components, a
coherent core and a halo, with
Ec  exp(  j )
EH  1  exp(  j )
• The width of the halo depends on the generalised
Fried parameter as follows:

 h  1.27
0
and the central peak Intensity is given by
2
2
 0    0  
I     1     exp(  j )
 D    D  
Modal Correction of PSF
Signal-to-Noise in AO corrected Images
• Detecting faint stars against background depends
on the signal-to-noise ratio (snr). This is defined
as the ratio of the mean signal to the standard
deviation. A detection usually requires SNR > 5.
• The main sources of noise in Astronomical images
are
– Background noise : Sky and thermal (IR)
– Detector noise
– Photon noise
AO advantage in point source detection
Consider observing with a telescope of diameter D meters.
The number of background photons detected in in t second
with a pixel of side a radians is given by
PB  N B D 2 a 2t
NB is the sky radiance in photons m-2 s-1 Sr-1
 is the overall quantum efficiency
For a point source of Irradiance HS photons m-2 s-1, the
number of photons detected in time t is
Ps  H S D 2t
Let b=the fraction of this signal within the pixel of side a,
so the Signal=bPS. From Poisson statistics:
noise  (bPs  PB )
AO advantage in point source detection
So the snr is given by
bPs
snr 
(bPs  PB )
For faint sources, with no AO assume pixel size matched to
seeing; a=2/r0
Ps  H S D 2t
snruncomp  H s D
r0
2
t
NB
With AO, change pixel size to match diffraction-limit; a=
2/D and the fraction of the point source flux in this pixel
is given by the Strehl Ratio, S
snrcomp
SD 2
 Hs
2
t
NB
AO advantage in point source detection
The Gain in SNR from AO is given by
G AO 
SD
r0
Example: D=10m, r0=1m, S=0.6 G=6
D=100m, r0=1m, S=0.4 G=40
In stellar magnitudes the gain is given by
M  2.5 log 10 (GAO )
The integration time to reach a given magnitude with the
same snr
1
t 2
G AO
These results are optimistic since AO usually reduces
throughput and increases the background
Wavefront Sensing
• The vast majority of AO systems employ a wavefront
sensor to measure wavefront phase errors (an alternative
approach is ‘dithering’).
• These are generally based on classical techniques of
optical testing. Do not necessarily give quantitative
measure of phase since usually works closed-loop i.e. Only
need to detect null condition.
• Most phase measurements are based either on
Interferometry or on Propagation
Phase Estimation
Aberrated
wavefront
R
Perfect
lens



u(r )  a(r ) expi (r )  t 
Phase Estimation using Interferometry
• Interference of two waves u1(r) and u2(r)

 2
 2




I (r )  a1 (r )  a2 (r )  2 a1 (r ) a2 (r ) cos(1 (r )   2 (r ))
• Point Diffraction Interferometer (PDI)
pinhole
Semi-transparent
Mach-Zehnder Interferometer
Pinhole
Detector 1
Detector 2
Ref: J.R.P. Angel, Nature vol. 368 p203 (1994)
Lateral Shear Interferometer



u1 (r )  a1 (r ) exp( i1 (r ))

 
 
u2 (r )  a1 (r  d ) exp( i1 (r  d ))
For small shear d
 

 
1 (r  d )  1 (r )  1 (r )  d  

 2
  2

 
 
I (r )  a1 (r )  a2 (r  d )  2 a1 (r ) a1 (r  d ) cos(1 (r )  d )
•Can vary sensitivity by adjusting d
•Does not need coherent reference
Wavefront sensing using propagation
Most wavefront sensing techniques rely on converting
wavefront gradients into measurable intensity variations. If
we write the complex amplitude as
A( x, y, z)  I ( x, y, z) exp( ikW ( x, y, z))
then the change in Irradiance along the propagation path is
given by
I
z
 (I .W  I 2W )
the first term is irradiance variation due to local tilt of the
wavefront. The second term is due to wavefront curvature.
The intensity changes are enhanced by placing a mask at one
plane and measuring the resulting intensity distribution at
another plane
Shack-Hartmann wavefront sensor
M
r
F
C
x
f
z

 



 
xn  I n1  xI ( x )d 2 ( x )  zI n1  A2 (r )W (r )  dr d 2 r
C
d
1 1

z f
m
Shack-Hartmann design
Telescope

’
f
 ' Dtel

 tel
 Darray f coll
•Also need sytem to select guide star in
field:
-pair of steering mirrors
-single mirror at reimaged pupil
-pick-off system
•May need to include an Atmospheric
Dispersion Corrector
•More optics if want to use with both
natural and laser guide stars (z ~ f2/H)
Collimator
microlens
array
’
f
b
Shack-Hartmann sensor gain
Output
Input tilt
Curvature Sensing
Recall Transport of Intensity equation
I
 (I .W  I 2W )
z
If in addition

I   (r  rc )n
then we have
I
 W  

 
 (r  rc )  I 2W 
z
 n

Curvature Sensing
l
P1
f
I 
I 2  I1
I 2  I1
2 f 2Cw
I 
l
F
P2
Curvature Sensing
l
P1
f
( f  l)
r0
r0l
f 2

l 
f
f  r02
Real curvature sensor....
Vibrating Membrane
Mirror
Bimorph DM
Lenslet array
Optical fibers
Computer
Avalanche
photodiodes
(APDs)
Pyramid Wavefront Sensor
P
F
f
Pyramid Wavefront Sensor
P
F
f
Pyramid wavefront sensor modulation
I2
I1
R
b1
I4
I3
S x ( xc, yc) 
b2
I1 ( xc, yc)  I 4 ( xc, yc)   I 2 ( xc, yc)  I 3 ( xc, yc) 
4
 I i ( xc, yc)
i 1
Sx 
b2  b1
2R
Canonical wavefront sensor
P
M
D
F
M
F
Periodic pattern of bars
Crossed cylinder lenses
Knife edge
1/4 wave retarding spot
Grating
Variable curvature mirror
Pyramid
Ronchi test
Shack-Hartmann
Schlieren
Zernike phase contrast
Shearing Interferometer
Curvature sensor
Pyramid sensor
Detectors employed in WFS
CCDs
• 80-90% QE over 450750nm
• stable geometry (up to
128x128 pixels
available for AO)
• SNR for faint sources
limited by readout
noise
– for AO 5e rms at 1
MHz
– Multiple ports
• Need cooling
APDs
• 85% QE at 0.5 m
• No read-out noise
• Can be electronically
gated
• One device = one
pixel (but faster than
charge transfer)
• Need active quenching
• Need cooling
Deformable mirror requirements
• Number of actuators
• Actuator spacing (pupil size)
• Actuator stroke (usually tip-tilt removed)
D

 r0 
  0.365
5
6
on D=10m, r0=10cm at 0.5 m; 3 =1.35m
•
•
•
•
•
•
Actuator influence function, interactuator coupling
Actuator Hysterisis
Temporal response (>1kHz)
Input voltage range
Surface quality (figure, smootness, reflectivity)
Probability of failure
Actuator types
• Piezoelectric (PZT)
– stack N elements to give range
– operates over wide temperature range
– hysterisis 10-20%
• Electrostrictive (PMN)
– low hysterisis at room temperature
– long term stability
– hysterisis is temperature dependent
• Magnetostrictive (Terfenol-D)
– 20% hysterisis
– operates over large temperature range
– long term stability
DM types
• Segmented
– piston only or piston-tip-tilt
•
•
•
•
•
Thin plate deformable mirrors
Bimorph mirrors
Deformable secondary mirrors
Membrane mirrors
Liquid crystal mirrors
DM types
faceplate
Discrete actuator
Bimorph
electrode
baseplate
Bimorph electrode size >
4x thickness
Difficult to make high order
Adaptive Secondary Mirrors
• Making the secondary mirror of the
telescope adaptive minimises emissivity
and maximises throughput
• Systems being developed for MMT and
LBT
• Mirror resonant frequency lower
• Maintenance difficult
• Calibration tricky
http://caao.as.arizona.edu/caao/
Performance Limitations
• The performance of real AO systems is limited by severaL
sources of error. These can be studied by detailed
numerical simulation or using approximate formulae.
• Consider errors in wavefront tip-tilt (expressed in radians
of tilt) seperately from remaining error, expressed in
radians.
• The corresponding Strehl ratios are given by
1
SRtilt 
1
   tilt 


2  c / D 
2
2
2
SRho  exp(  ho
)
• where  is the correction wavelength, D is the telescope
diameter. The final Strehl ratio is given by the product of
these:
SR  SRtiltSRho
Sources of error
• Noise in the wavefront sensor measurement
• Finite number of actuators in the deformable
mirror
• Delay between measuring and correcting
wavefront errors
• Angular offset between guide source and object of
interest
• Uncorrectable optical errors (in the telescope &
AO system)
• Scintillation
• .....
Noise in wavefront sensing
• A general expression for the phase measurement error due
to photon noise is
 2phot
1  d 

 
n ph   
2
where nph is the number of photons in the measurement,  is
the angular size of the guide source image, d is the
subaperture and  is the measurement wavelength. The
constant  depends on the details of the phase
measurement.
For faint sources the read noise dominates over the photon
noise.
Noise in wavefront sensing
• Bandwidth error
– The wavefront sensor has to integrate photons for a
finite amount of time before a measurement can be
made. In order to ensure stability, the closed-loop
bandwidth should not exceed 1/6 - 1/10 of the sampling
frequency.
– Greenwwod defined an effective turbulence bandwidth.
For a single turbulent layer moving at v ms-1
f G  0.427
v
r0
the wavefront error due to a finite servo bandwidth fs is
5
2
 bw
 f 3
   G 
 fS 
Optimal bandwidth
Note on calculating photons
Sometimes see very
optimistic estimates of
throughput....
Usually will not use a
standard filter in WFS
Deformable mirror fitting error
• Error due to the finite number of actuators in the
deformable mirror. For an actuator pitch (i.e. Separation)
of d, the error is given by:

2
fit
d
   
 r0 
5
3
where  depends on the type of deformable mirror and the
actuator geometry.
Influence
Actuators per 
function
subaperture
Piston only 1
1.26
Piston+tilt
3
Continuous 1
0.14
0.24-0.34
Finite Subaperture size
• Finite subaperture size leads to aliasing of high-frequency
wavefront errors into low-frequency errors.
d

 r0 
 2fit  0.08
5
3
• Usually, the subaperture size is made equal to the
deformable mirror actuator spacing. There is then a tradeoff between snr in the wavefront sensing and
fitting+aliasing errors
Optimal Subaperture Size
note: can simultaneousely optimise subaperture d and exposure time
Putting it all together
• Bright star Error Budget
S  STilt SbandwidthS fittingS aliasingSuncor Svib S ncp 
 2 
or equivalently
2
2
 2   bandw
  2fitting   alias

dominated by fitting and bandwidth error
Error budget for GTCAO
Tip – Tilt
Temporal
nrad
1.1
1.1
Rotator error
nrad
14
0
Centroid drift
nrad
19
0
nrad
24.0
1.1
0.946
1.0
Total
SRtip-tilt 2.2 microns
High Order
Bandwidth
nm
22
22
Time delay
nm
24.1
24.1
Scintillation
nm
35
35
Non-common path
optics
nm
30
30
Non-common path
thermal/gravitational
nm
49.5
0
Calibration
nm
35
35
Alignment
nm
8
8
Segment vibration
nm
60
60
WFS aliasing + DM
fitting + Uncorrected
telescope
nm
134.0
165.0
nm
169.0
188.0
SR high-order2.2 microns
0.793
0.75
SR total 2.2 microns
0.75
0.75
TOTAL High-order
What about faint stars ?
• Most systems specify a sky coverage; this
is tricky to verify as it depends on
isoplanatic angle and on your favourite
model of the sky distribution of stars
• It is more practical to specify a magnitude
limit for a given Strehl ratio e.g. S=0.1
For a perfect system