* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Photon scanning microscopy wikipedia , lookup
Depth of field wikipedia , lookup
Night vision device wikipedia , lookup
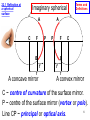
Birefringence wikipedia , lookup
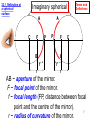
Surface plasmon resonance microscopy wikipedia , lookup
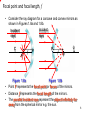
Ray tracing (graphics) wikipedia , lookup
Schneider Kreuznach wikipedia , lookup
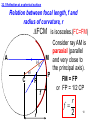
Reflecting telescope wikipedia , lookup
Nonimaging optics wikipedia , lookup
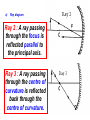
Anti-reflective coating wikipedia , lookup
Lens (optics) wikipedia , lookup
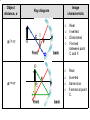
Retroreflector wikipedia , lookup
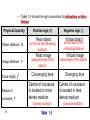
The study of light based on the assumption that light travels in straight lines and is concerned with the laws controlling the reflection and refraction of rays of light. CHAPTER 22: Geometrical optics (4 Hours) 1 UNIT 22 : GEOMETRICAL OPTICS 22.1 Reflection at a spherical surface 22.2 Refraction at a plane and spherical surfaces 22.3 Thin lenses 2 22.1 Reflection at a spherical surface At the end of this topic, students should be able to: ( 1 H) a) State laws of reflection. b) Sketch and use ray diagrams to determine the characteristics of image formed by spherical mirrors. c) Use 1 1 1 2 f u v r For real object only Use sign convention for focal length: + f for concave mirror and – f for convex mirror. Sketch ray diagrams with minimum two rays. r = 2f only applies to spherical mirror. 3 The Law of reflection The law of reflection states that • The incident ray, the reflected ray and normal, all lie in the same plane • The angle of incidence i is equal to the angle of reflection r. 4 22.1 Reflection at a spherical surface Terms and Definitions • A spherical mirror is a reflecting surface with spherical geometry. • Two types : i) convex, if the reflection takes place on the outer surface of the spherical shape. ii) concave, if the reflecting surface is on the inner surface of the sphere. 5 22.1 Reflection at a spherical surface Terms and Definitions Imaginary spherical A C A P F P F B B f r A concave mirror C f r A convex mirror C ~ centre of curvature of the surface mirror. P ~ centre of the surface mirror (vertex or pole). 6 Line CP ~ principal or optical axis. 22.1 Reflection at a spherical surface Terms and Definitions Imaginary spherical A C A P F P F B B f r C f r AB ~ aperture of the mirror. F ~ focal point of the mirror. f ~ focal length (FP, distance between focal point and the centre of the mirror). 7 r ~ radius of curvature of the mirror. Focal point and focal length, f • Consider the ray diagram for a concave and convex mirrors as shown in Figures 1.8a and 1.8b. Incident Incident rays rays C F f P P f C F Figure 1.8a Figure 1.8b • Point F represents the focal point or focus of the mirrors. • Distance f represents the focal length of the mirrors. • The parallel incident rays represent the object infinitely far away from the spherical mirror e.g. the sun. 8 Focal point or focus, F • For concave mirror – is defined as a point where the incident parallel rays converge after reflection on the mirror. – Its focal point is real (principal). • For convex mirror – is defined as a point where the incident parallel rays seem to diverge from a point behind the mirror after reflection. – Its focal point is virtual. Focal length, f • is defined as the distance between the focal point (focus) F and pole P of the spherical mirror. • The paraxial rays is defined as the rays that are near to and almost parallel to the principal axis. 9 22.1 Reflection at a spherical surface Relation between focal length, f and radius of curvature, r FCM is isosceles.(FC=FM) Consider ray AM is paraxial (parallel A M and very close to the principal axis). P FM = FP C F or FP = 1/2 CP f r r f 2 10 Ray diagrams for spherical mirrors is defined as the simple graphical method to indicate the positions of the object and image in a system of mirrors or lenses. Images formed by a concave mirror a) Ray diagram Ray 1 : A ray parallel to the principal axis is reflected through the focus (focal point). 11 a) Ray diagram Ray 2 : A ray passing through the focus is reflected parallel to the principal axis. Ray 3 : A ray passing through the centre of curvature is reflected back through the centre of curvature. 12 Images formed by a concave mirror Concave mirror can be used as a shaving and makeup mirrors because it provides an upright and virtual images. Table 1.1 shows the ray diagrams of locating an image formed by a concave mirror for various object distance, u. * Remember: At least any two rays for drawing the ray diagram 13 Object distance, u Image characteristic Ray diagram u>r C I P O F Front back O u=r F C P I 14 Front back Real Inverted Diminished Formed between point C and F. Real Inverted Same size Formed at point C. Object distance, u Image characteristic Ray diagram f<u<r I C P O F Front back O u=f 15 C Front Real Inverted Magnified Formed at a distance greater than CP. F P back Real or virtual Formed at infinity. Object distance, u Image characteristic Ray diagram u<f F C O P Front Virtual Upright Magnified Formed at the back of the mirror I back Table 1.1 16 Image formed by concave mirrors Notes i) If the object is at infinity, a real image is formed at F. Conversely, an object at F gives a real image at infinity. 5) Object at infinity F • • • • At F Real Inverted Smaller than object ii) In all cases, the foot of the object is on the principal axis and its image also lies on 17 this line. Image formed by a convex mirror Ray 1 : A ray parallel to the axis is reflected as though it came from the focal point. Ray 2 : A ray heading toward the focal point is reflected parallel to the axis. Ray 3 : A ray heading toward the centre of curvature is reflected back on itself. 18 Image formed by a convex mirror The characteristics of the image formed are virtual upright diminished (smaller than the object) formed at the back of the mirror (behind the mirror) Object position any position in front of the convex mirror. Convex mirror always being used as a driving mirror because it has a wide field of view and providing an upright image. 19 b) The mirror equation-calculation using formula A P B M v r u 20 b) The mirror equation-calculation using formula Object distance Image distance Radius of curvature Object size Image size Focal length = = = = = = OP IP CP OA IB f = = = = = u v r h h’ 1 1 1 f u v or 2 1 1 = + r u v 21 Linear Magnification, m Linear (lateral) magnification of the spherical mirror, m is defined as the ratio between image height, hi and object height, ho hi v m ho u where v : image distance from the pole u : object distance from the pole 22 • Table 1.2 shows the sign convention for spherical mirror’s equation . Physical Quantity u Image distance, v Focal length, f Object distance, Positive sign (+) Negative sign (-) Real object Virtual object (in front of the mirror) Real image (same side of the object) Concave mirror (at the back of the mirror) Virtual image (opposite side of the object) Convex mirror Table 1.2 • Note: – Real image is formed by the actual light rays that pass through the image. – Real image can be projected on the screen. 23 Example 22.1.1 : A dentist uses a small mirror attached to a thin rod to examine one of your teeth. When the tooth is 1.20 cm in front of the mirror, the image it forms is 9.25 cm behind the mirror. Determine a. the focal length of the mirror and state the type of the mirror used, b. the magnification of the image. Solution : Example 22.1.2: An upright image is formed 20.5 cm from the real object by using the spherical mirror. The image’s height is one fourth of object’s height. a. Where should the mirror be placed relative to the object? b. Calculate the radius of curvature of the mirror and describe the type of mirror required. c. Sketch and label a ray diagram to show the formation of the image. Solution : 25 Solution : 26 Solution : 27 Solution : 28 Example 22.1.3 : A person of 1.60 m height stands 0.60 m from a surface of a hanging shiny globe in a garden. a. If the diameter of the globe is 18 cm, where is the image of the person relative to the surface of the globe? b. How large is the person’s image? c. State the characteristics of the person’s image. Solution : 29 Solution : 30 Solution : 31 Example 22.1.4 : A shaving or makeup mirror forms an image of a light bulb on a wall of a bathroom that is 3.50 m from the mirror. The height of the bulb is 8.0 mm and the height of its image is 40 cm. a. Sketch a labeled ray diagram to show the formation of the bulb’s image. b. Calculate i. the position of the bulb from the pole of the mirror, ii. the focal length of the mirror. Solution : 32 3 Solution : Exercise : 1. a. A concave mirror forms an inverted image four times larger than the object. Calculate the focal length of the mirror, assuming the distance between object and image is 0.600 m. b. A convex mirror forms a virtual image half the size of the object. Assuming the distance between image and object is 20.0 cm, determine the radius of curvature of the mirror. ANS. : 160 mm ; 267 mm 2. a. A 1.74 m tall shopper in a department store is 5.19 m from a security mirror. The shopper notices that his image in the mirror appears to be only 16.3 cm tall. i. Is the shopper’s image upright or inverted? Explain. ii. Determine the radius of curvature of the mirror. b. A concave mirror of a focal length 36 cm produces an image whose distance from the mirror is one third of the object distance. Calculate the object and image distances. ANS. : u think, 1.07 m ; 144 cm, 48 cm 3. If a concave mirror has a focal length of 10 cm, find the two positions where an object can be placed to give, in each case, an image twice the height of the object.( 15cm, 5.0cm ) 4. A convex mirror of radius of curvature 40 cm forms an image which is half the height of the object. Find the object and image position.( 20cm,10cm behind the mirror ) 35 5. What are the nature, size, and location of the image formed when a 6 cm tall object is located 15 cm from a spherical concave mirror of focal length 20 cm ? (virtual, upright, -60 cm, + 24 cm) 36 22.2 Refraction at a plane and spherical surfaces (1 H) At the end of this chapter, students should be able to: State and use the laws of refraction (Snell’s Law) for layers of materials with different densities. Apply n1 n2 n2 n1 u v r for spherical surface. 37 22.2 Refraction at a plane and spherical surfaces 22.2.1 Refraction at a plane surface • Refraction is defined as the changing of direction of a light ray and its speed of propagation as it passes from one medium into another. • Laws of refraction state : – The incident ray, the refracted ray and the normal all lie in the same plane. – For two given media, Snell’s law states sin i n2 constant sin r n1 where 38 OR n1 sin i n2 sin r n1 : refractive index of the medium 1 (Medium containing the incident ray) n2 : refractive index of the medium 2 (Medium containing the refracted ray) r : angle of refraction • Examples for refraction of light ray travels from one medium to another medium can be shown in Figures 1.13a and 1.13b. (a) n1 n2 (b) n1 (Medium 1 is less dense medium 2) n2 (Medium 1 is denser than medium 2) Incident ray Incident ray i i n1 n2 n1 n2 r r Figure 1.13a 39 Refracted ray The light ray is bent toward the normal, thus r i Figure 1.13b Refracted ray The light ray is bent away from the normal, thus r i Refractive index (index of refraction), n • is defined as the constant ratio sin i for the two given media. sin r • The value of refractive index depends on the type of medium and the colour of the light. • It is dimensionless and its value greater than 1. • Consider the light ray travels from medium 1 into medium 2, the refractive index can be denoted by velocity of light in medium 1 v1 1 n2 velocity of light in medium 2 v2 (Medium containing the incident ray) 40 (Medium containing the refracted ray) • Absolute refractive index, n (for the incident ray travels from vacuum or air into the medium) is given by velocity of light in vacuum c n velocity of light in medium v • Table 1.3 shows the refractive indices for common substances. Substance Table 1.3 Solids (If the density of Diamond medium is Flint glass greater hence Crown glass Fused quartz (glass) the refractive Ice index is also Liquids greater) Benzene Ethyl alcohol Water Gases Carbon dioxide 41 Air Refractive index, n 2.42 1.66 1.52 1.46 1.31 1.50 1.36 1.33 1.00045 1.000293 Relationship between refractive index and the wavelength of light • As light travels from one medium to another, its wavelength, changes but its frequency, f remains constant. • The wavelength changes because of different material. The frequency remains constant because the number of wave cycles arriving per unit time must equal the number leaving per unit time so that the boundary surface cannot create or destroy waves. • By considering a light travels from medium 1 (n1) into medium 2 (n2), the velocity of light in each medium is given by then 42 v1 f1 and v2 f2 c v1 f1 where v1 n1 v 2 f2 and c v2 n2 c n1 1 c 2 n2 n11 n22 (Refractive index is inversely proportional to the wavelength) • If medium 1 is vacuum or air, then n1 = 1. Therefore the refractive index for any medium, n can be expressed as 0 n where 43 0 : wavelengt h of light in vacuum : wavelengt h of light in medium Example 22.2.1 : A fifty cent coin is at the bottom of a swimming pool of depth 3.00 m. The refractive index of air and water are 1.00 and 1.33 respectively. Determine the apparent depth of the coin. Solution : 44 Solution : 45 Solution : 46 Example 22.2.2 : A pond with a total depth (ice + water) of 4.00 m is covered by a transparent layer of ice of thickness 0.32 m. Determine the time required for light to travel vertically from the surface of the ice to the bottom of the pond. The refractive index of ice and water are 1.31 and 1.33 respectively. (Given the speed of light in vacuum is 3.00 108 m s-1.) Solution : 47 Solution : 48 22.2.2 Refraction at a spherical surface • Figure 1.14 shows a spherical surface with radius, r forms an interface between two media with refractive indices n1 and n2. i n1 B n2 PD O C I r u v Figure 1.14 • The surface forms an image I of a point object O. • The incident ray OB making an angle i with the normal and is refracted to ray BI making an angle where n1 < n2. 49 • Point C is the centre of curvature of the spherical surface and BC is normal. • From the figure, BOC BIC i (1) (2) • From the Snell’s law n1 sin i n2 sin By using BOD, BCD and BID thus BD BD BD tan ; tan ; tan OD CD ID By considering point B very close to the pole P, hence sin i i ; sin ; tan ; tan ; tan OD OP u ; CD CP r ; ID IP v then Snell’s law can be written as n1i n2 50 (3) • By substituting eq. (1) and (2) into eq. (3), thus then n1 ( ) n2 ( ) n1 n2 (n2 n1 ) BD BD BD n1 n2 (n2 n1 ) u v r n1 n2 (n2 n1 ) u v r where 51 Equation of spherical refracting surface v : image distance from pole u : object distance from pole n1 : refractive index of medium 1 (Medium containing the incident ray) n2 : refractive index of medium 2 (Medium containing the refracted ray) • Note : – If the refracting surface is flat (plane) : r then n1 n2 0 u v – The equation (formula) of linear magnification for refraction by the spherical surface is given by hi n1v m ho n2u 52 – Table 1.4 shows the sign convention for refraction or thin lenses: Physical Quantity Object distance, Image distance, Focal length, Radius of curvature, r f u v Positive sign (+) Real object (in front of the refracting surface) Real image (opposite side of the object) Converging lens Centre of curvature is located in more dense medium (convex surface) 53 Table 1.4 Negative sign (-) Virtual object (at the back of the refracting surface) Virtual image (same side of the object) Diverging lens Centre of curvature is located in less dense medium (concave surface) Example 22.2.3 : A cylindrical glass rod in air has a refractive index of 1.52. One end is ground to a hemispherical surface with radius, r =3.00 cm as shown in Figure 1.15. air glass P C O I 10.0 cm Figure 1.15 Calculate, a. the position of the image for a small object on the axis of the rod, 10.0 cm to the left of the pole as shown in figure. b. the linear magnification. (Given the refractive index of air , na= 1.00) 54 Solution : 55 Example 22.2.4: Figure 1.16 shows an object O placed at a distance 20.0 cm from the surface P of a glass sphere of radius 5.0 cm and refractive index of 1.63. Glass sphere air P O 5.0 cm 20.0 cm Figure 1.16 Determine a. the position of the image formed by the surface P of the glass sphere, b. the position of the final image formed by the glass sphere. 56 (Given the refractive index of air , na= 1.00) Solution : 57 Solution : 58 Solution : 59 Exercise : 1. A student wishes to determine the depth of a swimming pool filled with water by measuring the width (x = 5.50 m) and then noting that the bottom edge of the pool is just visible at an angle of 14.0 above the horizontal as shown in Figure 1.17. Figure 1.17 Calculate the depth of the pool. (Given nwater = 1.33 and nair = 1.00) ANS. : 5.16 m 60 2. A small strip of paper is pasted on one side of a glass sphere of radius 5 cm. The paper is then view from the opposite surface of the sphere. Determine the position of the image. (Given the refractive index of glass =1.52 and the refractive index of air =1.00) ANS. : 20.83 cm in front of the 2nd refracting surface. 3. A point source of light is placed at a distance of 25.0 cm from the centre of a glass sphere of radius 10 cm. Determine the image position of the source. (Given the refractive index of glass =1.52 and the refractive index of air =1.00) ANS. : 25.2 cm at the back of the 2nd refracting surface. 61 22.3 Thin lenses (2 hours) At the end of this chapter, students should be able to: • Sketch and use ray diagrams to determine the characteristics of image formed by diverging and converging lenses. • Use thin lens equation, 1 1 1 u v f • for real object only. Use lensmaker’s equation: 1 1 1 n 1 f r1 r2 62 • Use the thin lens formula for a combination of converging lenses. 22.3 Thin lenses • is defined as a transparent material with two spherical refracting surfaces whose thickness is thin compared to the radii of curvature of the two refracting surfaces. • There are two types of thin lenses. It is converging and diverging lenses. • Figures 1.18a and 1.18b show the various types of thin lenses, both converging and diverging. (a) Converging (Convex) lenses r1 (+ve) r 2 r1 (+ve)(+ve) Biconvex r2 r 1 () (+ve) Plano-convex 63 Figure 1.18a r2 (ve) Convex meniscus (b) Diverging (Concave) lenses r1 (ve) r2 r1 (ve) (ve) r2 r1 ()(+ve) Plano-concave Figure 1.18b Biconcave r2 (ve) Concave meniscus 17.4.1 Terms of thin lenses • Figures 1.19 show the shape of converging (convex) and diverging (concave) lenses. (a) Converging lens (b) Diverging lens r1 r1 C1 64 O r2 C2 C1 Figure 1.19 O r2 C2 • Centre of curvature (point C1 and C2) – is defined as the centre of the sphere of which the surface of the lens is a part. • Radius of curvature (r1 and r2) – is defined as the radius of the sphere of which the surface of the lens is a part. • Principal (Optical) axis – is defined as the line joining the two centres of curvature of a lens. • Optical centre (point O) – is defined as the point at which any rays entering the lens pass without deviation. 65 Focal point and focal length, f • Consider the ray diagrams for converging and diverging lenses as shown in Figures 1.20a and 1.20b. O F1 f F2 f O F1 f F2 f Figure 1.20a Figure 1.20b • From the figures, – Points F1 and F2 represent the focus of the lenses. – Distance f represents the focal length of the lenses. 66 Focus (point F1 and F2) • For converging (convex) lens – is defined as the point on the principal axis where rays which are parallel and close to the principal axis converges after passing through the lens. – Its focus is real (principal). • For diverging (concave) lens – is defined as the point on the principal axis where rays which are parallel to the principal axis seem to diverge from after passing through the lens. – Its focus is virtual. Focal length ( f ) • is defined as the distance between the focus F and the optical centre O of the lens. 67 Image Formation by Thin Lenses A thin lens is one whose thickness is small compared to its focal length, f . Ray diagrams can be drawn to determine the location and size of the image. 68 Ray Diagrams Image Formation by Thin Lenses Ray 1: A ray entering a converging lens parallel to its axis passes through the focal point F of the lens on the other side. Ray 2 : A ray entering a converging lens through its focal point exits parallel to its axis. Ray 3 : A ray passing through the center of the lens does not change direction. 69 Ray Diagrams Image Formation by Thin Lenses Ray 1: A ray entering a diverging lens parallel to its axis seems to come from the focal point F. Ray 2 : A ray that enters a diverging lens by heading toward the focal point on the opposite side exits parallel to its axis. Ray 3 : A ray passing through the center of the lens does not change direction. 70 Image Formation by Thin Lenses • If the image is real, the position of the image point is determined by intersection of any two rays 1, 2 and 3. • Real image is formed on the back side of the lens.(OPPOSITE SIDE) • If the image is virtual, we extend the diverging outgoing rays backward to their intersection point to seek the image point. • Virtual image is formed on the front side of the lens. (SAME SIDE) 71 Images formed by a converging lens • Table 1.5 shows the ray diagrams of locating an image formed by a converging lens for various object distance, u. Object distance, u Image characteristic Ray diagram Real Inverted Diminished Formed between point F2 and 2F2. (at the back of the lens) u > 2f 72 I O2F1 F1 F2 Front back 2F2 Object distance, u Image characteristic Ray diagram Real Inverted Same size Formed at point 2F2. (at the back of the lens) u = 2f O 2F2 F1 F2 Front back 2F1 I Real Inverted Magnified Formed at a distance greater f < u < 2f 2F1 O F1 Front 73 I F2 back 2F2 than 2f at the back of the lens. Object distance, u Image characteristic Ray diagram Real or virtual Formed at infinity. u=f O 2F1 F1 F2 Front back 2F2 Virtual Upright Magnified Formed in front of the lens. u<f I 74 2F1 F1 O Front Table 1.5 F2 back 2F2 Diverging Lens The image always , Image Formation by Thin Lenses a) Between lens and F1 a) Virtual b) Upright d) Smaller than object F1 75 Thin lens formula, lens maker’s and linear magnification equations Thin lens formula and lens maker’s equation • Considering the ray diagram of refraction for two spherical surfaces as shown in Figure 1.23. u1 r1 v2 D A n1 n2 C1 O 76 u2 t v1 r2 v1 Figure 1.23 P1 I1 B n1 C2 P2 E t I2 In general, 1 1 1 f u v Thin lens formula 1 n2 1 1 Lens maker’s 1 equation f n1 r1 r2 where f : focal length r1 : radius of curvature for 1stndrefracting surface r2 : radius of curvature for 2 refracting surface n1 : refractive index of the medium n2 : refractive index of the lens material 77 • Note : – If the medium is air (n1= nair=1) thus the lens maker’s equation can be written as 1 1 1 n 1 f r1 r2 – For thin lenses and lens maker’s equations, use the sign convention for refraction. where n : refractive index of the lens material Use sign convention for R : • +ve for convex surface • -ve for concave surface 78 78 Linear magnification, m • is defined as the ratio between image height, hi and object height, ho. • 79 hi v m ho u where v : image distance from optical centre u : object distance from optical centre 1 1 1 Since the linear magnification equation can be f u v written as 1 1 1 v f u v v v v 1 m 1 f u f Example 22.3.1 : A person of height 1.75 m is standing 2.50 m in from of a camera. The camera uses a thin biconvex lens of radii of curvature 7.69 mm. The lens made from the crown glass of refractive index 1.52. a. Calculate the focal length of the lens. b. Sketch a labeled ray diagram to show the formation of the image. c. Determine the position of the image and its height. d. State the characteristics of the image. Solution : 80 Solution : 81 Solution : 82 Example 22.3.2 : A thin plano-convex lens is made of glass of refractive index 1.66. When an object is set up 10 cm from the lens, a virtual image ten times its size is formed. Determine a. the focal length of the lens, b. the radius of curvature of the convex surface. Solution : 83 Solution : 84 Example 22.3.4 : The radii of curvature of the faces of a thin concave meniscus lens of material of refractive index 3/2 are 20 cm and 10 cm. What is the focal length of lens a. in air, b. when completely immersed in water of refractive index 4/3? Solution : 85 Solution : 86 Combination of lenses • Many optical instruments, such as microscopes and telescopes, use two converging lenses together to produce an image. • In both instruments, the 1st lens (closest to the object )is called the objective and the 2nd lens (closest to the eye) is referred to as the eyepiece or ocular. • The image formed by the 1st lens is treated as the object for the 2nd lens and the final image is the image formed by the 2nd lens. • The position of the final image in a two lenses system can be determined by applying the thin lens formula to each lens separately. • The overall magnification of a two lenses system is the product of the magnifications of the separate lenses. where m m1m2 m : overall magnificat ion 87 m1 : magnificat ion due to the 1stndlens m2 : magnificat ion due to the 2 lens Two Lenses System f = +20 cm B A p1 v1 p2 v2 88 First Step Two Lenses System • Let p1 represent the distance of object O from lens A. • Then find the distance v1 the image produced by lens A, either by using equation or drawing rays. 89 Second Step Two Lenses System • Ignore the presence of lens A, treat the image found in first step I1 as the object for lens B. • If this new object is located beyond lens B, the object distance p2 is taken to be negative. •If this new object is located in front of the lens B, the object distance p2 is taken to be positive. 90 Second Step Two Lenses System • The distance v2 of the final image (I2) produced by lens B can be found by using equation or drawing rays. • The overall linear magnification m produced by a system of two lenses is the product of the overall magnifications mA and mB produced by two lenses, m (mA )(mB ) 91 Example 22.3.5 : The objective and eyepiece of the compound microscope are both converging lenses and have focal lengths of 15.0 mm and 25.5 mm respectively. A distance of 61.0 mm separates the lenses. The microscope is being used to examine a sample placed 24.1 mm in front of the objective. a. Determine i. the position of the final image, ii. the overall magnification of the microscope. b. State the characteristics of the final image. Solution : 92 Solution : 93 Solution : 94 Solution : 95 Exercise: 1. a. A glass of refractive index 1.50 plano-concave lens has a focal length of 21.5 cm. Calculate the radius of the concave surface. b. A rod of length 15.0 cm is placed horizontally along the principal axis of a converging lens of focal length 10.0 cm. If the closest end of the rod is 20.0 cm from the lens calculate the length of the image formed. ANS. : 10.8 cm; 6.00 cm 2. An object is placed 16.0 cm to the left of a lens. The lens forms an image which is 36.0 cm to the right of the lens. a. Calculate the focal length of the lens and state the type of the lens. b. If the object is 8.00 mm tall, calculate the height of the image. c. Sketch a labelled ray diagram for the case above. ANS. : 11.1 cm; 1.8 cm 96 3. 97 When a small light bulb is placed on the left side of a converging lens, a sharp image is formed on a screen placed 30.0 cm on the right side of the lens. When the lens is moved 5.0 cm to the right, the screen has to be moved 5.0 cm to the left so that a sharp image is again formed on the screen. What is the focal length of the lens? ANS. : 10.0 cm 4. A converging lens of focal length 8.00 cm is 20.0 cm to the left of a converging lens of focal length 6.00 cm. A coin is placed 10.0 cm to the left of the 1st lens. Calculate a. the distance of the final image from the 1st lens, b. the total magnification of the system. ANS. : 24.6 cm; 0.924 5. A converging lens with a focal length of 4.0 cm is to the left of a second identical lens. When a feather is placed 12 cm to the left of the first lens, the final image is the same size and orientation as the feather itself. Calculate the separation between the lenses. ANS. : 12.0 cm