* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Normal Distribution
Survey
Document related concepts
Transcript
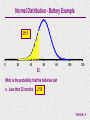
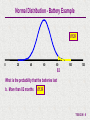
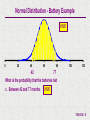
T06-02.N Normal Distribution Graphical Purpose Allows the analyst to analyze the Normal Probability Distribution. Probability Scenario's are calculated for "between", "greater than", and "less than" eliminating the need to perform calculations to use Standard Normal Distribution Tables. The template also allows the analyst to determine an X value depending upon a "Cumulative Probability". A graphical representation of the Probability Scenario is also shown. Inputs Mean & Standard Deviation of Normal Distribution Probability Scenario Outputs Probability Scenario Solution Graph of Probability Scenario T06-02.N - 1 Normal Distribution A normal probability distribution describes many random processes or continuous phenomena. It is the basis for classical statistical inference. 1 f(X) = e 2 f(X) x = = = = = X- 2 2 Frequency of random variable x Population standard deviation 3.14159; e = 2.71828 Value of random variable (- < x < ) Population mean T06-02.N - 2 Battery Example A manufacturer of batteries claims that the average length of life for its grade A batteries is 60 months. Suppose the standard deviation of the life-length is 10 months and the frequency distribution of the life-length data is normally distributed. What is the probability that the batteries last a. b. c. d. Less than 52 months More than 82 months Between 42 and 77 months Determine the battery life such that the probability less than the battery life is equal to .8400? T06-02.N - 3 Normal Distribution - Battery Example .2119 0 20 40 60 80 100 120 52 What is the probability that the batteries last a. Less than 52 months .2119 T06-02.N - 4 Input the mean, standard deviation, & probability scenario, and the answer and graph for the Normal Distribution probability scenario are automatically calculated T06-02.N - 5 Normal Distribution - Battery Example .0139 0 20 40 60 80 82 100 120 What is the probability that the batteries last b. More than 82 months .0139 T06-02.N - 6 Input the mean, standard deviation, & probability scenario, and the answer and graph for the Normal Distribution probability scenario are automatically calculated T06-02.N - 7 Normal Distribution - Battery Example .9195 0 20 40 60 80 100 120 42 77 What is the probability that the batteries last c. Between 42 and 77 months .9195 T06-02.N - 8 Input the mean, standard deviation, & probability scenario, and the answer and graph for the Normal Distribution probability scenario are automatically calculated T06-02.N - 9 Normal Distribution - Battery Example 0 20 40 60 69.945 80 100 120 Determine the battery life such that the probability less than the battery life is equal to .8400? In other words, What is the value of X such that CP(X) <= .8400? 69.945 T06-02.N - 10 Input the mean, standard deviation, & probability scenario, and the answer and graph for the Normal Distribution probability scenario are automatically calculated Caution: In using this portion of the template, you must enter the problem such that the input is the Cumulative Probability. T06-02.N - 11