Download Chapter 10 Section 1 (Confidence Intervals)

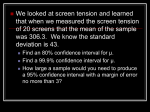
Section 10.1
Estimating with
Confidence
AP Statistics
February 11th, 2011
np  10 or nq  10?
Use Binomial distribution tools.
Sample Proportions?
Make sure the population size  10n
pq
n
so you may use  pˆ 
np  10 and nq  10?
Use Normal distribution tools.
Is the population distribution normal?
Use Normal distribution tools.
Sample Means?
Make sure the population size  10n
so you may use  x 

n
Is the shape of population distribution
unknown or distinctly nonnormal?
If n  25, the Central Limit Theorem
applies so you may use Normal distribution tools.
Otherwise, you need other tools.
An introduction to statistical
inference



Statistical Inference provides methods for
drawing conclusions about a population from
sample data.
In other words, from looking a sample, how
much can we “infer” about the population.
We may only make inferences about the
population if our samples unbiased. This
happens when we get our data from SRS or
well-designed experiments.
Example
A SRS of 500 California high school
seniors finds their mean on the SAT Math
is 461. The standard deviation of all
California high school seniors on this test
111.
 What can you say about the mean of all
California high school seniors on this
exam?

Example (What we know)
Data comes from SRS, therefore
unbiased.
 There are approximately 350,000
California high school seniors.
350,000>10*500. We can estimate sigmax-bar as sigma/root 500=4.5.
 The sample mean 461 one value in the
distribution of sample means.

Example (What we know)
The mean of the distribution of sample
means is the same as the population
mean.
 Because the n>25, the distribution of
sample means is approximately normal.
(Central Limit Theorem)

Our sample is just one value in a
distribution with unknown mean…
Confidence Interval

A level C confidence interval for a
parameter has two parts.
 An
interval calculated from the data, usually in
the form (estimate plus or minus margin of
error)
 A confidence level C, which gives the
probability that the interval will capture the
true parameter value in repeated samples.
Conditions for Confidence Intervals
the data come from an SRS or well
designed experiment from the population
of interest
 the sample distribution is approximately
normal

Confidence Interval Formulas
CI  x  z
CI  x  z
*

*

n
,x  z
*

n
n
*
where z is the upper p critical value
Using the z table…
Confidence
level
Tail Area
z*
90%
.05
1.645
95%
.025
1.960
99%
.005
2.576
or use the t-table at the back of the book
Confidence interval behavior

To make the margin
of error smaller…
 make
z* smaller,
which means you have
lower confidence
 make n bigger, which
will cost more
margin of error  z
*

n
Confidence interval behavior

If you know a
particular confidence
level and ME, you can
solve for your sample
size.
margin of error  z
*

n
Example


Company management
wants a report screen
tensions which have
standard deviation of 43
mV. They would like to
know how big the sample
has to be to be within 5
mV with 95% confidence?
You need a sample size
of at least 285.
ME  z
*

n
43
5  1.96
n
43
n  1.96
5
2
43 

n  1.96   284.12
5 

Review
Section 5.2
Experimental Design
AP Statistics
February 11th 2013
Statistical Significance

An observed effect so large that it would
rarely occur by chance is called
statistically significant.
Double-Blind

In a double-blind experiment, neither the
subjects nor the people who have contact
with know which treatment a subject
received.
Experiments without placebos

Matched pair design
 In
a matched pair design, subjects are paired
by matching common important attributes.
 Often the results are a pre-test and post-test
with the unit being “matched” to itself.
Block Design

A block is a group of experimental units or
subjects that are known before the
experiment to be similar in some way that
is expected to affect the response to the
treatments. In a block design, the random
assignment of units to treatments is
carried out separately within each block.
Section 10.2
Tests of Significance
AP Statistics
February 12th 2013
The Test of Significance

The test of significance asks the question:
 “Does
the statistic result from a real difference
from the supposition”
 or
 Does the statistic result from just chance
variation?”
Example
I claim that I make 80% of my free throws.
 To test my claim, you ask me to shoot 20
free throws.
 I make only 8 out of 20.
 You respond: “I don’t believe your claim. It
is unlikely that an 80% shooter makes only
8 of 20.”

Significance Test Procedure

Step 1: Define the population and parameter
of interest. State null and alternative
hypotheses in words and symbols.
 Population:
My free throw shots.
 Parameter of interest: proportion of made shots.
 Suppose I am an 80% shooter This is a
hypothesis, and we think that it is false. So we’ll
call it the null hypothesis, and use the symbol H0.
(Pronounced: H-nought) H0: p=.8
 You are trying to show that I’m worse than a 80%
shooter. Your alternate hypothesis is: Ha:
p<80%.
Significance Test Procedure

Step 2: Choose the appropriate inference
procedure. Verify the conditions for using
the selected procedure.
 We
are going to use the Binomial Distribution:
 Each trial has either success or failure.
 Set number of trials.
 Trials are independent.
 Probability of success is constant.
Significance Test Procedure

Step 3: Calculate the P-value. The P-value
is the probability that our sample statistics
is that extreme assuming that H0 is true.
 Look
at Ha to calculate “What is the
probability of making 8 or fewer shots out of
20?”
 X is the number of shots made.
 P(X<8)=.0001017=binomcdf(20,.8,8)
Significance Test Procedure

Step 4: Interpret the results in the context of
the problem.
 You
reject H0 because the probability of being an
80% shooter and making only 8 of 20 shots is
extremely low. You conclude that Ha is correct;
the true proportion is less than 80%.

There are only two possibilities at this step
 “We
reject H0 because the probability is so low.
We accept Ha.”
 “We fail to reject H0 because the probability is not
low enough.”
Significance Test Procedure
1.
2.
3.
Identify the population of interest and the
parameter you want to draw conclusions
about. State null and alternate hypotheses.
Choose the appropriate procedure. Verify
the conditions for using the selected
procedure.
If the conditions are met, carry out the
inference procedure.


4.
Calculate the test statistic.
Find the P-value
Interpret your results in the context of the
problem
Example
Diet colas use artificial sweeteners to avoid
sugar. These sweeteners gradually lose their
sweetness over time. Manufacturers
therefore test new colas for loss of sweetness
before marketing them. Trained tasters sip the
cola along with drinks of standard sweetness
and score the cola on a “sweetness score” of
1 to 10. The cola is then stored for a month at
high temperature to imitate the effect of four
months’ storage. Each taster scores the cola
again after storage.
 What kind of experiment is this?

Example
Here’s the data:
 2.0, .4, .7, 2.0, -.4, 2.2, -1.3, 1.2, 1.1, 2.3
 Positive scores indicate a loss of
sweetness.
 Are these data good evidence that the
cola lost sweetness in storage?

Significance Test Procedure

Step 1: Define the population and parameter
of interest. State null and alternative
hypotheses in words and symbols.
 Population:
Diet cola.
 Parameter of interest: mean sweetness loss.
 Suppose there is no sweetness loss (Nothing
special going on). H0: µ=0.
 You are trying to find if there was sweetness loss.
Your alternate hypothesis is: Ha: µ>0.
Significance Test Procedure

Step 2: Choose the appropriate inference
procedure. Verify the conditions for using the
selected procedure.
 We
are going to use sample mean distribution:
 Do the samples come from an SRS?
 We don’t know.
 Is the population at least ten times the sample size?
 Yes.
 Is the population normally distributed or is the sample size
at least 25.
 We don’t know if the population is normally distributed,
and the sample is not big enough for CLT to come into
play.
Significance Test Procedure

Step 3: Calculate the test static and the Pvalue. The P-value is the probability that our
sample statistics is that extreme assuming
that H0 is true.
x-bar=1.02, σ=1
 Look at Ha to calculate “What is the probability of
having a sample mean greater than 1.02?”
 z=(1.02-0)/(1/root(10))=3.226,
 P(Z>3.226) =.000619=normalcdf(3.226,1E99)
 µ=0,
Significance Test Procedure

Step 4: Interpret the results in the context of
the problem.
 You
reject H0 because the probability of having
a sample mean of 1.02 is very small. We
therefore accept the alternate hypothesis; we
think the colas lost sweetness.
Assignment
Exercises 10.27-10.37 odd, 10.45-10.55
odd
 Against All Odds Video www.learner.org,
Episode 20.
