Download Apply Central Limit Theorem to Estimates of Proportions

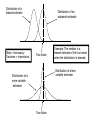
• Discrete distribution word problems
– Probabilities: specific values, >, <, <=, >=, …
– Means, variances
• Computing normal probabilities and “inverse”
values:
– Pr(X<y) when y is above and below the mean of X
– Pr(y1<X<y2) when y1 and y2 are:
• both above the mean of X
• both below the mean of X
• on opposite sides of the mean of X
• Central Limit Theorem:
– Sum version
– Average version
Apply Central Limit Theorem to
Estimates of Proportions
Source: gallup.com
Suppose this is
based on a poll of 100
people
number of people who answer favorable
pˆ 
number of people asked
xi  1 if person i says favorable,  0 otherwise
n
pˆ 
x
i 1
i
.
n
E ( xi )  p, Var ( xi )  p (1  p )
by CLT , as n  ,
Pˆ ~ N ( p, p (1  p ) / n)
This uses the “average”
version of the CLT. Two
lectures ago, we applied
the “sum” version of the
CLT to the binomial
distribution.
• Suppose true p is 0.40.
• If survey is conducted again on 49 people,
what’s the probability of seeing 38% to 42%
favorable responses?
Pr( 0.38 < P < 0.42)
= Pr[(0.38-0.40)/sqrt(0.62*0.38/49) < Z <
(0.42-0.40)/sqrt(0.62*0.38/49) ]
= Pr(-0.29 < Z < 0.29)
= 2*Pr(Z<-0.29)
= 0.77
Chapter 8:
• In the previous example, the random quantity
was the estimator.
• Examples of estimators:
Sample mean = X = (X1+…+Xn)/n
Sample variance = [(X1-X)2+…+(Xn-X)2]/(n-1)
Sample median = midpoint of the data…
Regression line = ….
ESTIMATORS CALCULATE
STATISTISTICS FROM DATA
If data are
random, then
the estimators are
random
too.
• Central limit theorem tells us that the
estimators X and P have normal
distributions as n gets large:
• X ~ N(m,s2/n) where m and s are the mean
and standard deviation of the random
variables that go into X.
• P ~ N(p,p(1-p)/n) where p is true
proportion of “yeses”
• Two ways of ways to evaluate estimators:
– Bias:
“Collect the same size data set over and over.
Difference between the average of the
estimator and the true value is the bias of the
estimator.”
– Variance:
Collect the same size data set over and over.
Variability is a measure of how closely each
estimate agrees.
Distribution of a
biased estimator
Bias = inaccuarcy
Variance = imprecision
Distribution of an
unbiased estimator
True value
Example: The median is a
biased estimate of the true mean
when the distribution is skewed.
Distribution of a less
variable estimator
Distribution of a
more variable
estimator
True value