* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 7_Step_Writeup
Survey
Document related concepts
Transcript
Tests of Significance
How to put them in writing.
As with confidence intervals, it is helpful to have a format to
follow to see that all steps are included.
Being able to write good answers to these questions is one of the
major goals of this course.
Once you learn this process, you will have to make only small
changes when we learn a new test, the framework will remain the
same.
The assumptions for confidence intervals are the same as those
for tests of significance.
Are you ready?
First we list the steps:
Step 1:
Null and alternate hypotheses
Step 2:
Assumptions
Step 3:
Formula and calculations
Step 4:
Graph
Step 5:
P-value
Step 6:
Reject/fail to reject and explain P-value.
Step 7:
Conclusion
We consider the problem of finding whether the average weight
of an ICR white laboratory mouse is the value we believe it to
be. We read that the mean and standard deviation are 37g and
3.2g, respectively. We collect a sample of 10 mice and record
these weights (in grams): {35, 42, 41, 34, 38, 36, 37, 39, 34,
36}. Like many other measurements, the weights of the mice
follow a normal distribution. The question we are asked is
whether the mean weight is 37g.
Now we will write an answer to this question, following the 7
steps.
We give more detail as we work:
Step 1:
Write the null and alternate hypotheses in
symbols, then in sentences, so that variables
are explained. Write an extra sentence or
make a legend if needed.
H0: =37g
Ha: 37g
H0: The mean weight for an adult ICR mouse is 37g.
Ha: The mean weight for an adult ICR mouse is not 37g.
For our problem,
Step 2:
Assumptions: meet every assumption
for the test.
We are given an SRS, a normal population, and is known.
Step 3:
Formula and calculations: Write the formula
for the calculation of the test statistic (Z) and
show the values substituted into the equation.
Solve for Z.
Z
x 0
n
37.2 37
.2
.1976
3.2
1.01192
10
n.b., 37.2 was found by calculating the mean of the data.
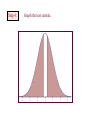
Step 4:
Graph the test statistic.
Step 5:
Calculate the probability of the shaded region
of the graph. Write a statement using Z.
P-value = P(Z .1976 or Z .1976)
2(.42166) .8433
Step 6:
Reject or fail to reject H0, followed by an
explanation of the meaning of the p-value.
Fail to reject H0, a test statistic this extreme
will occur by chance alone 84% of the time.
n. b., if you have trouble deciding whether to reject, ask
yourself if the result is surprising? Are you surprised that we
could get a mean of 37.2 when the true mean is 37? I’m not!
Step 7:
Write a conclusion in terms of the original
problem. I usually start with “We have
evidence of…” or “We lack evidence of…,”
and modify appropriately.
We lack evidence that the mean weight of ICR
mice is not 37 grams.
n.b., We either reject or fail to reject, but we never attempt to
prove that the null hypothesis is true!
Think about this for a minute.
We will have many variations, but the basic process will be the
same now for all tests of significance.
Remember the 7 steps:
Step 1:
Null and alternate hypotheses
Step 2:
Assumptions
Step 3:
Formula and calculations
Step 4:
Graph
Step 5:
P-value
Step 6:
Reject/fail to reject and explain P-value.
Step 7:
Conclusion
THE END