* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Mean Standard Deviation
Survey
Document related concepts
Transcript
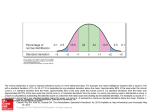
Interpreting Performance Data Expected Outcomes Understand the terms mean, median, mode, standard deviation Use these terms to interpret performance data supplied by EAU Measures of Central Tendency Mean … the average score Median … the value that lies in the middle after ranking all the scores Mode … the most frequently occurring score Measures of Central Tendency Which measure of Central Tendency should be used? Measures of Central Tendency The measure you choose should give you a good indication of the typical score in the sample or population. Measures of Central Tendency Mean … the most frequently used but is sensitive to extreme scores e.g. 1 2 3 4 5 6 7 8 9 10 Mean = 5.5 (median = 5.5) e.g. 1 2 3 4 5 6 7 8 9 20 Mean = 6.5 (median = 5.5) e.g. 1 2 3 4 5 6 7 8 9 100 Mean = 14.5 (median = 5.5) Measures of Central Tendency Median … is not sensitive to extreme scores … use it when you are unable to use the mean because of extreme scores Measures of Central Tendency Mode … does not involve any calculation or ordering of data … use it when you have categories (e.g. occupation) A Distribution Curve English Frequency 300 250 Mean: 54 200 Median: 56 150 Mode: 63 100 50 Mean = 53.78 Std. Dev. = 19.484 N = 4,253 0 0 20 40 60 English 80 100 The Normal Distribution Curve In everyday life many variables such as height, weight, shoe size and exam marks all tend to be normally distributed, that is, they all tend to look like the following curve. The Normal Distribution Curve Mean, Median, Mode 0.025 0.02 0.015 0.01 0.005 0 0 20 40 60 80 100 It is bell-shaped and symmetrical about the mean The mean, median and mode are equal It is a function of the mean and the standard deviation Variation or Spread of Distributions Measures that indicate the spread of scores: Range Standard Deviation Variation or Spread of Distributions Range It compares the minimum score with the maximum score Max score – Min score = Range It is a crude indication of the spread of the scores because it does not tell us much about the shape of the distribution and how much the scores vary from the mean Variation or Spread of Distributions Standard Deviation It tells us what is happening between the minimum and maximum scores It tells us how much the scores in the data set vary around the mean It is useful when we need to compare groups using the same scale Calculating a Mean and a Standard Deviation Sums Means Data x 10 20 30 40 50 150 30 Deviation x - Mean -20 -10 0 10 20 0 0 Standard deviation = Absolute Deviation |x - Mean| 20 10 0 10 20 60 12 Variance Squared Deviation (x-Mean)² 400 100 0 100 400 1000 200 Variance 14.1421356 Interpreting Distributions Mean 0.03 = 50 Std Dev = 15 0.025 0.02 0.015 34% 2% 0.01 0.005 34% 2% 14% 14% 0 0 10 20 30 40 50 60 70 80 90 100 scores 5 -3 0% 20 -2 2% 35 -1 16% 50 0 50% 65 +1 84% 80 +2 95 +3 sd 98% 100% rank Interpreting Distributions School A 50 10 Mean S.d. School B 60 10 School C 70 10 0 0.045 0.04 0.035 0.03 0.025 0.02 0.015 0.01 0.005 0 0 20 40 60 80 100 120 Interpreting Distributions School A 50 10 Mean S.d. School B 50 13 School C 50 16 0 0.045 0.04 0.035 0.03 0.025 0.02 0.015 0.01 0.005 0 0 20 40 60 80 100 120 Interpreting Distributions National Mean 55 10 Mean S.d. School A 60 15 School B 40 15 0.045 0.04 0.035 0.03 0.025 0.02 0.015 0.01 0.005 0 -20 0 20 40 60 80 100 120 The Z-score The z-score is a conversion of the raw score into a standard score based on the mean and the standard deviation. z-score = Raw score – Mean Standard Deviation Example z-score Mean = 55 65 – 55 15 = 0.67 Standard Deviation = 15 Raw Score = 65 Converting z-scores into Percentiles Use table provided to convert the z-score into a percentile. z-score = 0.67 Percentile = 74.86% (from table provided) Interpretation: 75% of the group scored below this score. Comparing School Performance with National Performance Mean S.d. National Mean 55 10 School A 60 15 School B 40 15 0.045 Z-score for Mean of School A = (60 – 55)/10 = 0.2 0.04 0.035 0.03 0.025 0.02 0.015 0.01 0.005 0 A z-score of 0.2 is equivalent to a percentile of 57.93% on a national basis Z-score for Mean of School B = (40 – 55)/10 = -1.5 A z-score of –1.5 is equivalent to a percentile of -20 0 20 40 60 80 100 120 (100-93.32)%, that is, 6.68%!