* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch 10
Survey
Document related concepts
Transcript
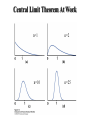
Chapter 10 Sampling and Sampling Distributions • • • • • 10.1 Random sampling 10.4 Stratified sampling 10.6 Sampling distribution 10.7 The standard error of the mean 10.8 The central limit theorem 10.1 Random sampling • Example: At a parts depot the inventory shows 1000 parts in stock. What percentage of those are actually in stock? – Let p = true % – To estimate p, take a sample of n parts to check out in the supply room. – Then pˆ sample proportion – How do we choose the parts to check? Random sample • A random sample is an insurance policy to protect against bias. • A simple random sample gives each of the N n possible sample choices the same chance of being selected. Random sampling In other words, for a finite population of N sample points: A sample of size n is random if any n sample points have a probability 1 N n to be selected. To generalize For an infinite population, or a finite population but sampling with replacement. A value is observed according to a probability distribution. A random sample of size n consists of observed values that are independent and have the same distributions. 10.2 &10.3 Skip 10.4 Stratified sample • A simple random sample is not always the best option. • Consider the following example. We want to estimate the average number of vireos per area. Conifer Desiduous Then the population mean and sample mean are total red-eyed vireos total area total observed red-eyed vireos x total observed area Question: if we use simple random sampling, is x always a good estimator of ? • Answer: NO. • Reasoning: A simple random sample of n=10 locations might all end up Conifer. We would be better off putting n1 samples in conifer and n2 samples in Desiduous. Stratified sampling • A stratified random sample breaks the population into strata and samples randomly within each stratum. • In our previous example: – Stratum 1 = Deciduous – Stratum 2 = Conifer Notations N1=number of units in stratum 1 N2=number of units in stratum 2 N = N1+N2 = number of units in entire population n1=number of units sampled from stratum 1 n2=number of units sampled from stratum 2 n = n1+n2 = number of sampled units Optimal allocation • How do we decide n1 and n2 (when n is fixed)? N1=# of possible sampling locations in conifer N2=# in desiduous σ1=standard deviation of bird counts in conifer σ2=standard deviation of bird counts in desiduous Optimal allocation: (Problem 10.29) nN1 1 n1 N1 1 N 2 2 nN 2 2 n2 N1 1 N 2 2 Sample more in strata, with --more units (area) --higher variability Proportional allocation • Proportional allocation doesn’t consider σ and makes the sample number from each stratum proportional to the size of the stratum. N1 n1 n N1 N 2 N2 n2 n N1 N 2 Example of proportional allocation If N1=100 Then N2=300 N1 100 1 N1 N 2 400 4 1 n1 40 10 4 3 n2 40 30 4 n=40 A comparison between simple random sampling and stratified sampling Example: Population: Weights of rocks 4, 6, 10, 12. So N=4 and =8. Sample n=2. Possible results for simple random samples Sample 4 6 4 10 4 12 6 10 6 12 10 12 Probability 1/6 1/6 1/6 1/6 1/6 1/6 sample mean 5 7 8 8 9 11 Probability 1/6 1/6 2/6 1/6 1/6 Example Continued • Possible results for a stratified sample. Choose 1 from the smaller rocks and choose 1 from the larger rocks. Sample 4 10 4 12 6 10 6 12 Probability 1/4 1/4 1/4 1/4 sample mean 7 8 8 9 Probability 1/4 1/2 1/4 A comparison between simple random sampling and stratified sampling 2/5 3/5 1/3 2/5 1/5 Series2 Series2 1/5 0 0 0 5 6 7 8 SRS 9 10 11 7 8 9 Stratified The stratified sample is more likely to be close to the true population value, 8 here. 10.6 Sampling Distributions A statistic (e.g. sample mean) from a random sample or randomized experiment is a random variable and its probability distribution is a sampling distribution. The population distribution of a variable is the distribution of its values for all members of the population. The population distribution is also the probability distribution of the variable when choosing one subject at random from the population. Sampling Variability Approximating the Sampling Distribution Results of many random samples of size n=100, from a population where it is known that 60% of the people hate to shop for clothes, population proportion (parameter) p = .6) and sample proportion p̂ (statistic). Most samples of size n = 100 gave estimates close to .6, but some were far off. On average, they centered on .6, they are variable, but unbiased. Sampling Variability (cont.) Approximating the Sampling Distribution Results of many random samples of size n=2500, from the same population, with population proportion (parameter) p = .6) and sample proportion p̂ (statistic). Larger samples are more precise (have less variability) AND are unbiased. Sample size What advantage is there of taking a larger sample? Larger n? Taking a larger sample decreases the potential deviation of away from . Let x be the standard deviation of the sampling distribution of x , then the larger the sample size is, the smaller x is. x Unbiased estimators • P.77 “Estimators having the desirable property that their values will on average equal the quantity they are supposed to estimate are said to be unbiased.” • If x then x is an unbiased estimator of . • Another example of unbiased estimator is s2 for 2. • Choosing non-random samples can introduce bias. 10.7 The Standard Error of the Mean If x is the mean of a sample of size n from a population having mean and standard deviation . The mean and standard deviation of x are: x x n (standard error of the mean) N n for finite populations or x n N 1 So, as n increases, x decreases. If the sample size is multiplied by 4, the “standard deviation” (standard error of the mean) will be divided in half for infinite populations. Standard Deviation vs. Standard Error of the Mean • The standard error of the mean is smaller than the standard deviation by a factor of the square root of the sample size. • The standard deviation describes the variability of individuals. • The standard error of the mean describes the accuracy of means of a given size or the potential error in sample mean as a guess at . Examples • Population size N=4, sample size n=2, 110 150 112 152 131 20.025 What is the standard error of the mean? 20.025 4 2 x 11.56 4 1 2 Examples • Infinite Population P(3)=P(5)= P(7)=P(9)= 1/4 6 5 2 What is the standard error of the mean? x 5 1.58 2 Example • Governor’s Poll Estimate guess 1, 1, 1 0, 1, 0 0, … x observed fraction of 1' s p̂ What is the standard error of the mean? fraction of 1s p 2 (0 ) 2 P(0) (1 ) 2 P(1) (0 p ) 2 (1 p ) (1 p) 2 p p 2 (1 p)[ p 1 p] p (1 p ) x pˆ Related to variance of a binomial x p(1 p) n If a population has the N(,) distribution, then the sample mean x distribution. of n independent observations has the N ( , ) n 10.8 Central Limit Theorem For ANY population with mean and standard deviation the sample mean x of a random sample of size n is approximately N ( , n ) when n is LARGE. Central Limit Theorem If the population is normal or sample size is large, sample mean x follows a normal distribution N ( , and z n ) x x x x n follows a standard normal distribution. • The closer x’s distribution is to a normal distribution, the smaller n can be and have the sample mean nearly normal. • If x is normal, then the sample mean is normal for any n, even n=1. Central Limit Theorem At Work n=1 n=2 n=10 n=25 • Usually n=30 is big enough so that the sample mean is approximately normal unless the distribution of x is very asymmetrical. • If x is not normal, there are often better procedures than using a normal approximation, but we won’t study those options. Example • X=ball bearing diameter • X is normal distributed with =1.0cm and =0.02cm • x =mean diameter of n=25 • Find out what is the probability that x will be off by less than 0.01 from the true population mean. x 1.0 0.02 x 0.004 n 25 0.99 1.0 1.01 1.0 P(0.99 x 1.01) P( z ) 0.004 0.004 P(2.5 z 2.5) 98.76% Exercise The mean of a random sample of size n=100 is going to used to estimate the mean daily milk production of a very large herd of dairy cows. Given that the standard deviation of the population to be sampled is s=3.6 quarts, what can we assert about he probabilities that the error of this estimate will be more then 0.72 quart?