Download Chapter 7: The Distribution of Sample Means

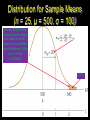
COURSE: JUST 3900
INTRODUCTORY STATISTICS
FOR CRIMINAL JUSTICE
Chapter 7:
The Distribution of Sample Means
Instructor:
Dr. John J. Kerbs, Associate Professor
Joint Ph.D. in Social Work and Sociology
© 2013 - - DO NOT CITE, QUOTE, REPRODUCE, OR DISSEMINATE WITHOUT
WRITTEN PERMISSION FROM THE AUTHOR:
Dr. John J. Kerbs can be emailed for permission at [email protected]
Samples and Populations



Samples provide an incomplete picture of the
population.
There are aspects of the population that may not be
included within a sample.
The sampling error is the natural discrepancy (i.e.,
the difference), or amount of error, between a sample
statistic and its corresponding population parameter.
 The sampling error is the measure of the
discrepancy (i.e., difference) between the sample
and the population.
A Sampling Distribution

A Sampling Distribution is a distribution of
statistics obtained by selecting all of the
possible samples of a specific size (n) from
a population.
The Distribution of Sample Means

The Distribution of Sample Means is defined
as the set of sample means for all of the
possible random samples of a particular size
(n) that can be selected from a specific
population.
Often called the Sampling Distribution of M
 This distribution has well-defined (and predictable)
characteristics that are specified in the Central
Limit Theorem

The Distribution of Sample Means

The three characteristics of the Distribution of Sample
Means
 1. Sample means should pile up around the population
mean
 2. The pile of sample means should tend to form a normalshaped distribution. They should pile up in the center of
the distribution (around μ) and the frequencies should
taper off as the distance between M and μ increases.
 3. In general, the larger the sample, the closer the sample
means should be to the population mean (μ).



Larger samples are more representative of the population than
smaller samples
Sample means obtained with large samples (i.e., a large n) should
cluster relatively close to the population parameter
Means obtained by small samples should be more widely scattered
The Central Limit Theorem
 The
Central Limit Theorem is defined as
follows:
 For any population with a mean (μ) and
standard deviation (σ), the distribution of
sample means for sample size n will have a
mean of μ and a standard deviation of σ
and will approach a normal distribution as
n approaches infinity (∞).
The Central Limit Theorem
1. The Expected Value of M is the mean of the distribution
of sample means and the Expected Value of M is always
equal to the mean of the population of scores (μ).
2. The shape of the distribution of sample means tends to
be normal. It is guaranteed to be normal if either a) the
population from which the samples are obtained is
normal, or b) the sample size n ≥ 30.
3. The standard deviation of the distribution of sample
means is called the Standard Error of M (σM) and is
computed by the following:
The Expected Value of M
If two (or more) samples are selected from the
same population, the two samples probably
will have different means.
 Although the samples will have different
means, you should expect the sample mans to
be close to the population mean.
 The mean of the distribution of the sample of
means is equal to the mean of the population
of scores (μ): that is the expected value of M.

Standard Error of M



The standard error (also known as the standard deviation of
the distribution of sample means, σM) provides a measure of
the average distance between M (sample mean) and μ
(population mean).
σM describes the distribution of sample means (variability)
 σM shows how much distance is expected between M and μ
Law of large numbers: The larger the sample size (n), the
more probable or likely it is that M is close to μ.
 Inverse relationship: the larger the sample size, the smaller
the stander error.
 Small standard errors indicate that sample means are close
together (large standard errors indicate that means are
scattered over a large range with larger difference from one
sample to another)
The Standard Error of M
The standard error of M is defined as the
standard deviation of the distribution of sample
means and measures the standard distance
between a sample mean and the population
mean.
 Thus, the Standard Error of M provides a
measure of how accurately, on average, a
sample mean represents its corresponding
population mean.

The Standard Error of M
Consider the changes in Standard
Error of M as n increases from 1 to 4
and then to 100 for a normal
population with a mean of 80 (μ=80)
and a standard deviation of 20 (σ=20)
Do NOT confuse
“standard deviations”
with
“standard errors”
Difference Between Standard Deviations
and Standard Errors



Standard Deviation measures the distance between a score
and the population mean
 X-μ
The Standard Error measures the distance between a sample
mean and the population mean
 M–μ
The Standard Error (σM) is the same as the Standard
Deviation for n = 1
 Note: there is only one population mean
Probability and Sample Means
Because the distribution of sample means
tends to be normal, the z-score value obtained
for a sample mean can be used with the unit
normal table to obtain probabilities.
 The procedures for computing z-scores and
finding probabilities for sample means are
essentially the same as we used for individual
scores

Probability and Sample Means
(cont'd.)
However, when you are using sample means,
you must remember to consider the sample
size (n) and compute the standard error (σM)
before you start any other computations.
 Also, you must be sure that the distribution of
sample means satisfies at least one of the
criteria for normal shape before you can use
the unit normal table:

1. the population from which the samples are
obtained is normal, or
 2. the sample size (n) is 30 or more.

z-Scores and Location within the
Distribution of Sample Means

Within the distribution of sample means, the
location of each sample mean can be specified
by a z-score:
(M – μ)
z = ───── or
σM
z =
(M – μ)
─────
(σ/√n)
z-Scores and Location within the
Distribution of Sample Means
(Continued)
As always, a positive z-score indicates a
sample mean that is greater than μ and a
negative z-score corresponds to a sample
mean that is smaller than μ.
 The numerical value of the z-score indicates
the distance between M and μ measured
in terms of the standard error.

Distribution for Sample Means
(n = 25, μ = 500, σ = 100)
A score of 540 is two
standard errors above
the mean (z=+2.00),
which is very unlikely
(see Unit Normal Table
for z = +2.00,
p = 0.0228)
2.28%
More Thoughts on
Standard Error


Standard errors are nothing more than measures of reliability.
Vogt (2005, p. 274) defines reliability as follows:
 Freedom from measurement (random) error. In practice,
this boils down to consistency or stability of a measure or
test or observation from one use to the next. When
repeated measures of the same thing give highly similar
results, the measurement instrument is said to be reliable.
 Small standard errors indicate that sample means are
close together and so researchers can be fairly
confident that an individual sample mean can act as a
reliable measure of the population mean
 Large standard errors indicate problems with reliability