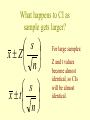Download Confidence Interval for Mean

Confidence Interval for a Mean
when you have a “small” sample...
As long as you have a
“large” sample….
A confidence interval for a population mean is:
 s 
x  Z

 n
where the average, standard deviation, and n depend
on the sample, and Z depends on the confidence level.
Example
Random sample of 59 students spent an
average of $273.20 on Spring 1998 textbooks.
Sample standard deviation was $94.40.
 94.4 
273.20  1.96
  273.20  24.09
 59 
We can be 95% confident that the average amount spent
by all students was between $249.11 and $297.29.
What happens if you can only
take a “small” sample?
• Random sample of 15 students slept an
average of 6.4 hours last night with standard
deviation of 1 hour.
• What is the average amount all students
slept last night?
If you have a “small” sample...
Replace the Z value with a t value to get:
 s 
x  t 

 n
where “t” comes from Student’s t distribution,
and depends on the sample size through the
degrees of freedom “n-1”.
Student’s t distribution versus
Normal Z distribution
T-distribution and Standard Normal Z distribution
0.4
Z distribution
density
0.3
0.2
T with 5 d.f.
0.1
0.0
-5
0
Value
5
T distribution
• Shaped like standard normal distribution
(symmetric around 0, bell-shaped).
• But, t depends on the degrees of freedom
“n-1”.
• And, more likely to get extreme t values
than extreme Z values.
Graphical Comparison of
T and Z Multipliers
5
4
T with 5 df
3
2
Z distribution
1
0
0.90
0.92
0.94
0.96
0.98
Cumulative Probability
1.00
Tabular Comparison of
T and Z Multipliers
Confidence t value with Z value
level
5 d.f
2.015
1.65
90%
2.571
1.96
95%
4.032
2.58
99%
For small samples, T value is larger than Z value.
So,T interval is made to be longer than Z interval.
Back to our example!
Sample of 15 students slept an average of 6.4
hours last night with standard deviation of 1 hour.
Need t with n-1 = 15-1 = 14 d.f.
For 95% confidence, t14 = 2.145
 s 
 1 
x  t
  6.4  2.145
  6.4  0.55
 n
 15 
That is...
We can be 95% confident that average amount
slept last night by all students is between 5.85
and 6.95 hours.
Hmmm! Adults need 8 hours of sleep each
night.
Logical conclusion:
On average, students need more sleep.
(Just don’t get it in this class!)
T-Interval for Mean in Minitab
T Confidence Intervals
Variable
Comb
N
89
Mean
2.011
StDev
1.563
SE Mean
0.166
95.0 % CI
(1.682, 2.340)
We can be 95% confident that the average number of
times a “Stat-250-like” student combs his/her is
between 1.7 and 2.3 times a day.
T- interval in Minitab
•
•
•
•
•
•
Select Stat.
Select Basic Statistics.
Select 1-Sample t…
Select desired variable.
Specify desired confidence level.
Say OK.
What happens as
sample gets larger?
T-distribution and Standard Normal Z distribution
0.4
Z distribution
density
0.3
T with 60 d.f.
0.2
0.1
0.0
-5
0
Value
5
What happens to CI as
sample gets larger?

x  Z


x  t

s 

n
s 

n
For large samples:
Z and t values
become almost
identical, so CIs
will be almost
identical.
Example
Random sample of 64 students spent an average of 3.8
hours on homework last night with a sample standard
deviation of 3.1 hours.
Z Confidence Intervals The assumed sigma = 3.10
Variable
Homework
N
Mean
64 3.797
StDev
3.100
95.0 % CI
(3.037,
4.556)
T Confidence Intervals
Variable N
Mean
Homework 64 3.797
StDev
3.100
95.0 % CI
(3.022,
4.571)
One not-so-small problem!
• It is only OK to use the t interval for small
samples if your original measurements
are normally distributed.
• We’ll learn how to check for normality.
Strategy
• If you have a large sample of, say, 30 or
more measurements, then don’t worry about
normality, and calculate a t-interval.
• If you have a small sample and your data
are normally distributed, then calculate a
t-interval.
• If you have a small sample and your data
are not normally distributed, then stay
tuned.