Download Chemical Analysis - Wake Forest University

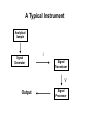
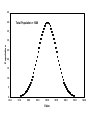
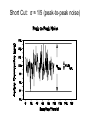
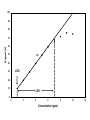
Spectrochemical Analysis
Qualitative Analysis
Quantitative Analysis
Determination
“Analyze” a paint sample for lead
“Determine” lead in a paint sample
Bulk Material
↓
Sample
↓
Analytical Sample
↓
Analytical Matrix
↓
Analyte + Concomitants
BLANK
Same concomitants
No analyte
Difficult if not impossible to
acquire a true blank
INSTRUMENTAL ANALYSIS
1) Electroanalytical Chemistry
2) Spectrochemical Analysis
3) Chromatographic Separations
A Typical Instrument
Analytical
Sample
Signal
Generator
i
Signal
Transducer
V
Output
Signal
Processor
Types of Signals
1.
2.
3.
4.
5.
6.
Emission of Radiation
Absorption of Radiation
Scattering of Radiation
Refraction of Radiation
Diffraction of Radiation
Rotation of Radiation
7.
8.
9.
10.
11.
12.
13.
Electrical Potential
Electrical Current
Electrical Resistance
Mass-to-charge Ratio
Reaction Rate
Thermal Properties
Mass
Signal Sources
1)
2)
3)
4)
Analytical Signal
Blank Signal
Background Signal
Dark Signal
Measured Signal:
A combination
of these
Analytical Figures of Merit
“Indicate a characteristic of an instrumental
technique for a given analyte”
“7”
Accuracy, Precision, Signal-to-Noise Ratio
Sensitivity, Limit of Detection
Linearity, Linear Dynamic Range
Accuracy
Indicates how close the measured value is
to the true analytical concentration
Requires a Standard Reference Material
(SRM) of other official measure
NIST: National Institute of Standards and
Technology
Accuracy
Most commonly reported as percent error
│Cm - Ct│
Ct
x 100%
where:
Cm = measured concentration
Ct = true concentration
Precision
Indicates the reproducibility of repetitive
measurements of equivalent samples
May be expressed as:
1. Standard Deviation (s or σ)
2. Relative Standard Deviation (RSD)
3. Confidence Limits
Precision
Standard Deviation
For an infinite number of measurements (σ)
For a finite number of measurements (s)
Standard Deviation
Note that both s and σ have the same units
as the original values
How many values should be obtained?
Rule of thumb: 16
45
40
Total Population = 1000
35
Population
30
25
20
15
10
5
0
96.0
97.0
98.0
99.0
100.0
Value
101.0
102.0
103.0
104.0
1.00%
How far is the measured mean from the true value?
0.90%
0.80%
Error in Mean
0.70%
0.60%
0.50%
0.40%
0.30%
0.20%
0.10%
0.00%
0
5
10
15
20
25
30
Number of Samples
35
40
45
50
70.0%
How far is s from σ?
60.0%
Error in Std. Dev.
50.0%
40.0%
30.0%
20.0%
10.0%
0.0%
0
5
10
15
20
25
30
Number of Samples
35
40
45
50
Short Cut: σ ≈ 1/5 (peak-to-peak noise)
Relative Standard Deviation
RSD = σ/mean
Where the mean may be the signal or the
analyte concentration. RSD is a unit-less
value, so σ must have the same units as
the mean.
RSD is often reported as %RSD, and may be
used to compare different techniques.
Confidence Limits
Define an interval that encloses
the true value (Ct) with a
specified level of confidence.
1. Cm ± σ
66.7% Confidence Level
2. Cm ± 2σ
95% Confidence Level
3. Cm ± 3σ
99.0% Confidence Level
Signal to noise Ratio (S/N)
S/N = Sm/σ = 1/RSD
Notes:
1. N = noise (σ)
2. S/N is unitless
3. Always try top maximize S/N
4. S/N is used to compare instruments
5. A plot of S/N versus an instrumental parameter reaches
a maximum at the optimum value for that parameter
Sensitivity
Experimental slope of a calibration curve
m = ΔS/ΔC
Sensitivity is almost always specific for one
particular instrument.
100
90
80
Signal (V)
70
60
50
m
40
LOD
30
20
10
LDR
0
0
2
4
6
Concentration (ppm)
8
10
12
Limit of Detection
The analyte concentration yielding an
analytical signal equal to 3 times the
standard deviation in the blank signal.
LOD = 3 x σbl / m
By definition, the LOD has just one
significant figure!!
Linearity
Measure of how well the observed data
follows a straight line.
SA = mC
SA = Analytical Signal
m = calibration sensitivity
Remember SA = Stot - Sbl
Linearity
Plot log(S) versus log(C)
log(SA) = log(m) + log(C)
The slope of this plot should be 1.00
A calibration curve is defined as linear if the
log-log plot has a slope in the range 0.95-1.05
Linear Dynamic Range
The concentration range over which the
calibration curve is linear
Lower End → LOD
Upper End
Analyte Concentration where the observed
signal falls 5% below the extrapolated line
LDR Units are
“orders of magnitude”
or
“decades”
of analyte concentration
LDR is easiest to observe on log-log plot
If linearity is poor, define an analytically
useful range (AUR)
Other figures of merit may be calculated,
but these 7 are sufficient.
Selectivity and Resolution may be useful
in cases where more than one analyte is
determined in the same sample.