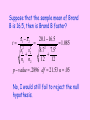* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Two-Sample Inference Procedures
Foundations of statistics wikipedia , lookup
History of statistics wikipedia , lookup
Sufficient statistic wikipedia , lookup
Confidence interval wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Taylor's law wikipedia , lookup
Resampling (statistics) wikipedia , lookup
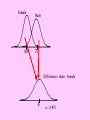
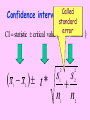
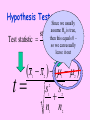
Two-Sample Inference Procedures with Means Remember: x y x y x y 2 2 x y We will be intereste d in the differen ce of means, so we will use this to find standard error. Suppose we have a population of adult men with a mean height of 71 inches and standard deviation of 2.6 inches. We also have a population of adult women with a mean height of 65 inches and standard deviation of 2.3 inches. Assume heights are normally distributed. Describe the distribution of the difference in heights between males and females (malefemale). Normal distribution with x-y =6 inches & x-y =3.471 inches Female 65 Male 71 Difference = male - female 6 = 3.471 a) What is the probability that the height of a randomly selected man is at most 5 inches taller than the height of a randomly selected woman? P((xM-xF) < 5) = normalcdf(-∞,5,6,3.471) = .3866 b) What is the 70th percentile for the difference (male-female) in heights of a randomly selected man & woman? (xM-xF) = invNorm(.7,6,3.471) = 7.82 Do calculator simulation! a) What is the probability that the mean height of 30 men is at most 5 inches taller than the mean height of 30 women? b) What is the 70th percentile for the difference (male-female) in mean heights of 30 men and 30 women? Two-Sample Procedures When we with means compare, • what are we The goal of these inferenceinterested procedures is to compare the in? responses to two treatments or to compare the characteristics of two populations. • We have INDEPENDENT samples from each treatment or population Assumptions: • Have two SRS’s from the populations or two randomly assigned treatment groups • Samples are independent • Both distributions are approximately normal – Have large sample sizes – Graph BOTH sets of data • ’s unknown Formulas Since in real-life, we will NOT know both ’s, we will do t-procedures. Degrees of Freedom Option 1: use the smaller of the two values n1 – 1 and n2 – 1 This will produce conservative results – higher p-values & lower confidence. Calculator Option 2: approximation used bydoes this automatically! technology s s 2 2 1 2 1 2 2 n n df 1 s 1 s n 1 n n 1 n 1 2 2 1 2 1 2 2 Confidence Called intervals: standard error CI statistic critical value SD of statistic s s x x t * n n 1 2 2 1 2 1 2 2 Pooled procedures: • Used for two populations with the same variance • When you pool, you average the two-sample variances to estimate the common population variance. • DO NOT use on AP Exam!!!!! We do NOT know the variances of the population, so ALWAYS tell the calculator NO for pooling! Two competing headache remedies claim to give fastacting relief. An experiment was performed to compare the mean lengths of time required for bodily absorption of brand A and brand B. Assume the absorption time is normally distributed. Twelve people were randomly selected and given an oral dosage of brand A. Another 12 were randomly selected and given an equal dosage of brand B. The length of time in minutes for the drugs to reach a specified level in the blood was recorded. The results follow: mean SD n Brand A 20.1 8.7 12 Brand B 18.9 7.5 12 Describe the shape & standard error for sampling distribution of the differences in the mean speed of absorption. (answer on next screen) Describe the sampling distribution of the differences in the mean speed of absorption. Normal distribution with S.E. = 3.316 Find a 95% confidence interval difference in mean lengths of time required for bodily absorption of each brand. Note: confidence interval statements • Matched pairs – refer to “mean difference” • Two-Sample – refer to “difference of means” Hypothesis Statements: H0: Ha: Ha: Ha: 1 = - 2 = 0 1 < 2 < 0 1 > 2 > 0 1 ≠ 2 ≠ 0 Be sure to define BOTH 1 and 2! Hypothesis Test: Test statistic Since we usually assume H0 is true, statistic parameter then this equals 0 – can usually SDsoofwestatistic leave it out x x t 1 2 1 2 2 1 2 1 2 s s n n 2 The length of time in minutes for the drugs to reach a specified level in the blood was recorded. The results follow: Brand A Brand B mean 20.1 18.9 SD 8.7 7.5 n 12 12 Is there sufficient evidence that these drugs differ in the speed at which they enter the blood stream? Have 2 independent randomly assigned treatments State assumptions! Given the absorption rate is normally distributed ’s unknown H0: A= B Ha:A= B On Calc: Go to Stat – Test Input Statistics No Pooling Calculate Hypotheses & define variables! Where A is the true mean absorption time for Brand A & B is the true mean absorption time for Brand B x1 x2 20.1 18.9 t .361 2 s12 s22 Formula 8.7 2 & 7.5calculations n1 n2 12 12 p value .7210 Conclusion df 21.53 in α context .05 Since p-value > a, I fail to reject H0. There is not sufficient evidence to suggest that these drugs differ in the speed at which they enter the blood stream. Suppose that the sample mean of Brand B is 16.5, then is Brand B faster? t x1 x2 s12 s22 n1 n2 20.1 16.5 8.7 2 7.52 12 12 1.085 p value .2896 df 21.53 α .05 No, I would still fail to reject the null hypothesis. Robustness: • Two-sample procedures are more robust than one-sample procedures • BEST to have equal sample sizes! (but not necessary) A modification has been made to the process for producing a certain type of time-zero film (film that begins to develop as soon as the picture is taken). Because the modification involves extra cost, it will be incorporated only if sample data indicate that the modification decreases true average development time by more than 1 second. Should the company incorporate the modification? Original 8.6 5.1 4.5 5.4 Modified 5.5 4.0 3.8 6.0 6.3 6.6 5.8 4.9 5.7 8.5 7.0 5.7 Assume we have 2 independent SRS of film Both distributions are approximately normal due to approximately symmetrical boxplots ’s unknown H0: O- M = 1 Where O is the true mean developing time for original film & M is the true mean developing time for modified film Ha:O- M > 1 t x1 x2 1 2 6.3375 5.3375 1 0 s s n1 n2 2 1 2 2 1.5146 1.0636 8 8 2 p value .5 df 7 .05 Since p-value > , I fail to reject H0. There is not sufficient evidence to suggest that the company incorporate the modification. 2