* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download HashingFinal
Survey
Document related concepts
Transcript
Dictionaries, Tables
Hashing
TCSS 342
1/51
The Dictionary ADT
• a dictionary (table) is an abstract model of a
database
• like a priority queue, a dictionary stores
key-element pairs
• the main operation supported by a
dictionary is searching by key
2/51
Examples
•
•
•
•
Telephone directory
Library catalogue
Books in print: key ISBN
FAT (File Allocation Table)
3/51
Main Issues
• Size
• Operations: search, insert, delete, ??? Create
reports??? List?
• What will be stored in the dictionary?
• How will be items identified?
4/51
The Dictionary ADT
• simple container methods:
– size()
– isEmpty()
– elements()
• query methods:
– findElement(k)
– findAllElements(k)
5/51
The Dictionary ADT
• update methods:
– insertItem(k, e)
– removeElement(k)
– removeAllElements(k)
• special element
– NO_SUCH_KEY, returned by an unsuccessful
search
6/51
Implementing a Dictionary
with a Sequence
• unordered sequence
– searching and removing takes O(n) time
– inserting takes O(1) time
– applications to log files (frequent insertions,
rare searches and removals) 34 14 12 22 18
34
14
12
22
18
7/51
Implementing a Dictionary
with a Sequence
• array-based ordered sequence
(assumes keys can be ordered)
- searching takes O(log n) time (binary search)
- inserting and removing takes O(n) time
- application to look-up tables
(frequent searches, rare insertions and removals)
12
14
18
22
34
8/51
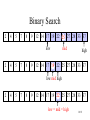
Binary Search
• narrow down the search range in stages
• “high-low” game
• findElement(22)
2
low
4
5
7
8
9 12 14 17 19 22 25 27 28 33 37
mid
high
9/51
Binary Search
2
4
5
7
8
9 12 14 17 19 22 25 27 28 33 37
low
2
4
5
7
8
mid
high
9 12 14 17 19 22 25 27 28 33 37
low mid high
2
4
5
7
8
9 12 14 17 19 22 25 27 28 33 37
low = mid = high
10/51
Pseudocode for Binary Search
Algorithm
BinarySearch(S, k, low, high)
if low > high then
return NO_SUCH_KEY
else
mid (low+high) / 2
if k = key(mid) then
return key(mid)
else if k < key(mid) then
return BinarySearch(S, k, low, mid-1)
else
return BinarySearch(S, k, mid+1, high)
11/51
Running Time of Binary
Search
• The range of candidate items to be searched
is halved after each comparison
Comparison
Search Range
0
n
1
n/2
…
…
2i
n/2i
log 2n
1
12/51
Running Time of Binary
Search
• In the array-based implementation, access
by rank takes O(1) time, thus binary search
runs in O(log n) time
• Binary Search is applicable only to Random
Access structures (Arrays, Vectors…)
13/51
Implementations
• Sorted? Non Sorted?
• Elementary: Arrays, vectors linked lists
– Orgainization: None (log file), Sorted, Hashed
• Advanced: balanced trees
14/51
Skip Lists
• Simulate Binary Search on a linked list.
• Linked list allows easy insertion and
deletion.
• http://www.epaperpress.com/s_man.html
15/51
Hashing
• Place item with key k in position h(k).
• Hope: h(k) is 1-1.
• Requires: unique key (unless multiple items
allowed). Key must be protected from
change (use abstract class that provides only
a constructor).
• Keys must be “comparable”.
16/51
Key class
•
•
•
•
•
•
•
public abstract class KeyID {
Private Comparable searchKey;
Public KeyID(Comparable m) {
searchKey = m;
}//Only one constructor
public Comparable getSearchKey() {
return searchKey;
}
• }
17/51
Hash Tables
• RT&T is a large phone company, and they
want to provide enhanced caller ID
capability:
–
–
–
–
given a phone number, return the caller’s name
phone numbers are in the range 0 to R = 1010–1
n is the number of phone numbers used
want to do this as efficiently as possible
18/51
Alternatives
• There are a few ways to design this dictionary:
• Balanced search tree (AVL, red-black, 2-4 trees,
B-trees) or a skip-list with the phone number as
the key has O(log n) query time and O(n) space --good space usage and search time, but can we
reduce the search time to constant?
• A bucket array indexed by the phone number has
optimal O(1) query time, but there is a huge
amount of wasted space: O(n + R)
19/51
Bucket Array
• Each cell is thought of as a bucket or a container
– Holds key element pairs
– In array A of size N, an element e with key k is inserted
in A[k].
Table operations without searches!
(null)
(null)
000-000-0000 000-000-0001
…
Roberto
401-863-7639 ...
Note: we need 10,000,000,000 buckets!
…
(null)
999-999-9999
20/51
Generalized indexing
• Hash table
– Data storage location associated with a key
– The key need not be an integer, but keys must
be comparable.
21/51
Hash Tables
• A data structure
• The location of an item is determined
– Directly as a function of the item itself
– Not by a sequence of trial and error comparisons
• Commonly used to provide faster searching.
• Comparisons of searching time:
– O(n) for linear searches
– O (logn) for binary search
– O(1) for hash table
22/51
Examples:
•
•
A symbol table constructed by a compiler.
Stores identifiers and information about
them in an array.
File systems:
– I-node location of a file in a file system.
•
Personal records
– Personal information retrieval based on key
23/51
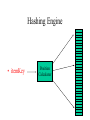
Hashing Engine
• itemKey
Position
Calculator
24/51
Example
• Insert item (401-863-7639, Roberto) into a table of size 5:
• calculate: 4018637639 mod 5 = 4, insert item (401-8637639, Roberto) in position 4 of the table (array, vector).
• A lookup uses the same process: use the hash engine to
map the key to a position, then check the array cell at that
position.
401863-7639
Roberto
0
1
2
3
4
25/51
Chaining
• The expected, search/insertion/removal time
is O(n/N), provided the indices are
uniformly distributed
• The performance of the data structure can
be fine-tuned by changing the table size N
26/51
From Keys to Indices
• The mapping of keys to indices of a hash table is
called a hash function
• A hash function is usually the composition of two
maps:
– hash code map: key integer
– compression map: integer [0, N - 1]
• An essential requirement of the hash function is to
map equal keys to equal indices.
• A “good” hash function is fast and minimizes the
probability of collisions
27/51
Perfect hash functions
• A perfect hash function maps each key to a
unique position.
• A perfect hash function can be constructed
if we know in advance all the keys to be
stored in the table (almost never…)
28/51
A good hash function
1. Be easy and fast to compute
2. Distribute items evenly throughout the
hash table
3. Efficient collision resolution.
29/51
Popular Hash-Code Maps
• Integer cast: for numeric types with 32 bits
or less, we can reinterpret the bits of the
number as an int
• Component sum: for numeric types with
more than 32 bits (e.g., long and double),
we can add the 32-bit components.
30/51
Sample of hash functions
• Digit selection:
h(2536924520) = 590
(select 2-nd, 5-th and last digits).
This is usually not a good hash function. It
will not distribute keys evenly.
A hash function should use every part of the
key.
31/51
Sample (continued)
• Folding: add all digits
• Modulo arithmetic:
h(key) = h(x) = x mod table_size.
The modulo arithmetic is a very popular basis
for hash functions. To better the chance of
even distribution table_size should be a
prime number. If n is the number of items
there is always a prime p, n < p < 2n.
32/51
Popular Hash-Code Maps
• Polynomial accumulation: for strings of a
natural language, combine the character
values (ASCII or Unicode) a 0 a 1 ... a n-1 by
viewing them as the coefficients of a
polynomial: a 0 + a 1 x + ...+ a n-1 x n-1
• For instance, choosing x = 33, 37, 39, or 41
gives at most 6 collisions on a vocabulary
of 50,000 English words.
33/51
Popular Hash-Code Maps
• Why is the component-sum hash code bad
for strings?
34/51
Popular Compression Maps
• Division: h(k) = |k| mod N
– the choice N =2 k is bad because not all the bits are
taken into account
– the table size N is usually chosen as a prime
number
– certain patterns in the hash codes are propagated
• Multiply, Add, and Divide (MAD):
– h(k) = |ak + b| mod N
– eliminates patterns provided a mod N 0
– same formula used in linear congruential (pseudo)
random number generators
35/51
Java Hash
• Java provides a hashCode() method for the
Object class, which typically returns the 32bit memory address of the object.
• This default hash code would work poorly
for Integer and String objects
• The hashCode() method should be suitably
redefined by classes.
36/51
Collision
• A collision occurs when two distinct items
are mapped to the same position.
• Insert (401-863-9350, Andy) 0
• And insert (401-863-2234, Devin).
4018632234 4. We have a collision!
401863-9350
Andy
0
401863-7639
Roberto
1
2
3
4
37/51
Collision Resolution
• How to deal with two keys which map to
the same cell of the array?
• Need policies, design good Hashing engines
that will minimize collisions.
38/51
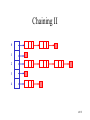
Chaining I
• Use chaining
– Each position is viewed as a container of a list
of items, not a single item. All items in this list
share the same hash value.
39/51
Chaining II
0
1
2
3
4
40/51
Collisions resolution policies
• A key is mapped to an already occupied table
location
– what to do?!?
• Use a collision handling technique
– Chaining (may have less buckets than items)
– Open Addressing (load factor < 1)
• Linear Probing
• Quadratic Probing
• Double Hashing
41/51
Linear Probing
• If the current location is used, try the next
table location
• linear_probing_insert(K)
if (table is full) error
probe = h(K)
while (table[probe] occupied)
probe = (probe + 1) mod M
table[probe] = K
42/51
Linear Probing
• Lookups walk along table until the key or an
empty slot is found
• Uses less memory than chaining
– don’t have to store all those links
• Slower than chaining
– may have to walk along table for a long way
• Deletion is more complex
– either mark the deleted slot
– or fill in the slot by shifting some elements down
43/51
Linear Probing Example
• h(k) = k mod 13
• Insert keys:
• 18 41 22 44 59 32 31 73
0
1
2
3
4
5
41
0
1
2
6
7
8
9
10 11 12
18 44 59 32 22 31 72
3
4
5
6
7
8
9
10 11 12
44/51
Double Hashing
• Use two hash functions
• If M is prime, eventually will examine every
position in the table
• double_hash_insert(K)
if(table is full) error
probe = h1(K)
offset = h2(K)
while (table[probe] occupied)
probe = (probe + offset) mod M
table[probe] = K
45/51
Double Hashing
• Many of same (dis)advantages as linear
probing
• Distributes keys more uniformly than linear
probing does
46/51
Double Hashing Example
• h1(K) = K mod 13
• h2(K) = 8 - K mod 8
– we want h2 to be an offset to add
– 18 41 22 44 59 32 31 73
– h1(44) = 5 (occupied) h2(0) = 8 44 5+8 Mod 13
0
1
44
0
2
3
4
41 73
1
2
3
5
6
7
8
9
10 11 12
18 32 53 31 22
4
5
6
7
8
9
10 11 12
47/51
Why so many Hash functions?
• “Its different strokes for different folks”.
• We seldom know the nature of the object
that will be stored in our dictionary.
48/51
A FAT Example
• Directory: Key: file name. Data (time, date, size
…) location of first block in the FAT table.
• If first block is in physical location #23 (Disk
block number) look up position #23 in the FAT.
Either shows end of file or has the block number
on disk.
• Example: Directory entry: block # 4
• FAT: x x x F 5 6 10 x 23 25
3
The file occupies blocks 4,5,6,10, 3.
49/51