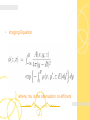Download Ch 9

Chapter 9
Emission Computed Tomography
Shi Chen
What is Emission Computed
Tomography?
• Definition
It is a type of tomography involving radioactive emissions which requires
computed tomography image reconstruction methods.
• Two Types include
positron emission tomography (PET)
– Uses radiotracers that generate positron decay
– Positron decay produces two photons in two opposite directions at a time
– Use special coincidence detection circuitry to detect two photons in
opposite directions simultaneously
single-photon emission computed tomography (SPECT)
– Use radiotracers that generate gammay decay
– Capture photons in multiple directions, similar to X-ray CT
– obtain projection data from multiple angles
9.1 Instrumentation
9.1.1 SPECT Instrumentation
• specialized ring detector systems
consist of an array of individual detectors that surround the patient.
Ring systems produce excellent tomograms.
very expensive and relatively rare.
• rotating Anger cameras
mounted on a special ganrty that allows 360-degree rotation around the patient.
popular.
SPECT Collimator
• Collimator
The collimator defines the kind of projection and determines the
direction of the incident photon for any scintillation in the crystal.
• The types of collimators
parallel-hole, converging, diverging, and pinhole.
• Two types of collimators are used in SPECT
parallel-hole
fan-beam(like converging collimators)
multiple Anger camera detectors
• multiple Anger camera detectors(so-called heads)
It is perhaps the biggest recent advance in SPECT systems because
adding camera heads increases sensitivity.
• Benefits provided
1. decrease noise while using the same acquisition time as with
single-head system
2. decrease acquisition time to get the same counts as a single-head
system
3. It may be "traded" for higher resolution through the use of higher
resolution/lower sensitivity collimators
comparison between dual-head and
single-head
360°
180°
Acquisition
Times
Relative
Sensitivities
Acquisition
Times
Relative
Sensitivities
single
30
1
30
1
double
(heads@180°
)
15
2
30
1
double
(heads@90°)
15
2
15
2
triple
10
3
20
1.5
table 9.1 in p304
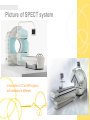
Picture of SPECT system
it looks like a CT or MRI system
but hardware is different
9.1.2 PET Instrumentation
When a positron is emitted, it travels up to several millimeters in the tissue,
depositing its kinetic energy. It then meets a free electron in the tissue, and
mutual annihilation occurs. Two photons appear and are emitted back-toback(180° apart).
• It's possible to use a single-head Anger camera to
individually detect one of the two 511keV gamma ray
photons that are emitted by positron-electron
annihilation.
• But it's more advantageous to detect the two gamma
rays at the same time. (Annibilation coincidence
detection, ACD)
– Because direction is automatically provided by 2 co-linear
photons
– Consequently, we do not need any collimator
• Dual-head SPECT scanners can be used for PET. But
because of positioning uncertainty increases when the
same camera is used for lower energy SPECT and the
inefficient angular acquisition, dual-head SPECT
scanners are not the ideal solution for PET.
Full-fledged PET system
Geometry of a multiple-ring PET system
Geometry of a PET detector block
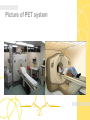
Picture of PET system
9.2 Image Formation
9.2.1 SPECT Image Formation
• Coordinate systems
laboratory coordinate system + rotating coordinate system
We use A(x,y,z) to denote the
radioactivity within the 3-D body,
and want A(x,y) to represent a
reconstructed cross-section for a
fixed z position.
• Imaging Equation
where, mu is the attenuation co-efficient
• Reconstruction
The convolution back-projection formula for SPECT is given by

A( x, y)  
0
c



c
 (, )c( x cos
  y sin   )dd
is an approximate ramp filter
1
1D
c()  F {| Q | W (Q)}
9.2.2 PET Image Formation
• Coordinate systems
We consider only 2-D PET for ease of understanding, the
reconstruction of axial cross-section from data collected within isolated
axial detector rings.
Integration geometry for PET imaging equation
• Imaging Equation
9.2.3 Iterative Reconstruction
• Basic concept
The reconstruction of an image from the acquired data is an
inverse problem.
Often, it is not possible to exactly solve the inverse problem
directly.
In this case, a direct algorithm has to approximate the solution,
which might cause visible reconstruction artifacts in the image.
Iterative algorithms approach the correct solution using multiple
iteration steps, which allows to obtain a better reconstruction at the
cost of a higher computation time.
9.3 Image Quality in SPECT and PET
9.3.1 Spatial Resolution
• Definition
- Spatial resolution in PET and SPECT derive from the desire to specify
that distance by which two objects must be separated to perceive them as
discrete.
- In an ideal detection device, an infinitely small isotopic source might be
rendered graphically as a vertical line whose infinitely narrow width reflected
perfect spatial resolution.
- When viewed in an actual PET or SPECT scanner, however, radioactivity
from such a point source is spread-out and appears as a Gaussian curve.
- This so-called point (or line) spread function (psf) characterizes a camera's
resolving capacity AND reflects the degree of spatial diffusion of imaged
radioactivity.
9.3.2 Attenuation and Scatter
• Attenuation
A significant number of high-energy g photons escape detection by PET and
SPECT scanners as a result of their interactions with surrounding tissues.
The physical basis for attenuation effects derives from the interaction of g
rays with atomic electrons. In Compton scattering, a g photon is deflected
from its original trajectory after colliding with an electron and loses a fraction
of its original energy in the process. Alternatively, collision may instead
result in the complete absorption of a photon's energy. In the latter instance,
the imparted kinetic energy is generally sufficient to eject the electron from
the atom, and thus g radiation is said to be ionizing.
Photon attenuation is less problematic for PET than for SPECT. Since
photons in PET have higher energies
• Scatter
Accurate reconstruction in PET and SPECT depends on the detection of
high-energy photons that travel in a straight path. However, Compton
effects cause photons to deviate from their original trajectories. Since many
scattered photons retain a sufficient degree of energy to escape from the
body, the detection of scattered events leads to the misinterpretation of
photon trajectories and produces errors in image reconstruction. The net
effect of such errors is similar to that of accidental coincidences, namely an
increase in background noise that compromises image contrast.
• Random Coincidences
These occur when one annihilation photon from one electron-positron
annihilation event, and another annihilation photon from a different
electron-positron annihilation event are detected in coincidence.
random coincidence count rate:
R  2S S


where 2 is the coincidence time window width and S+ and S- are the
individual count rates of opposing detectors.
• Contrast
differences between the image intensity of an object and
surrounding objects or background.
• In SPECT and PET, fmax and fmin are from reconstructed
images
• Noise and signal-to-noise
Noise arises from:
(1) the random statistical nature of radioactive decay, as well as
(2) potentially from the imaging hardware and
(3) certain image processing operations, and influences the "noise"
component of the ratio.
That's all
• Thanks
• References
- Medical Imaging Signals and Systems, chapter 9.
- Web,Yao Wang, Medical Imaging, chapter 8,9.
- Robert T. Malison, Marc Laruelle, and Robert B. Innis Positron and Single Photon
Emission Tomography