Download What Are Numbers? Angela Kramer Professor David Brown Ithaca College

What Are Numbers?
Angela Kramer
Professor David Brown
Ithaca College
May 8, 2013
Abstract
What are numbers? Throughout this paper I will seek to answer this question, by exploring
numbers from a variety perspectives. I will discuss numbers through exploration of two historic
number systems, through formal creation of the real number line, as well as geometric construction of numbers. I will also look at numbers by using a non-numerical approach based on sets.
I will also briefly investigate how we came to use the numerals we use today.
1
Contents
1
Introduction
3
2
Mayan Number System
3
2.1
Mayan Addition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.2
Mayan Subtraction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.3
Mayan Multiplication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.4
Mayan Division . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
3
Babylonian Number System
10
4
Zero
13
5
Constructing the Real Number Line
15
5.1
Rational Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
5.2
Real Numbers from Cauchy Sequences . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5.3
The Reals as an Ordered Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5.4
Dedekind Cuts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
6
Constructible Numbers
20
7
A Non-Numerical Approach
23
8
Roots of Hindu-Arabic Numerals
25
9
Conclusion
26
References
27
2
1 Introduction
In school, one of the first things that children learn is how to count, using the natural numbers like
0, 1, 2, 3, so on and so forth. Eventually they learn about the negative numbers, -1, -2, -3, and so
on, by subtracting a large number from a smaller number. As they move on through school kids
learn about rational numbers, or a number that can be represented in fraction form with
a
b
where
a and b are both integers. From there, children learn about irrational numbers, so they can use
the whole real number line, and eventually complex numbers.
But what is a number, and how do we represent it? There is clearly a difference between the
form of a number, or the symbolic numeral, 7 for example, and the meaning, for example *******.
Some children try to make a connection between what a numeral looks like and what it means as a
number. For example, a child might see a numeral 4, and count the number of line segments that it
takes to create a numeral 4, and derive the meaning that 4 represents ****, as shown in Figure 1.
Figure 1: This shows the connection between the form and meaning of the numeral four.
Similarly, !^* to us represents 3 symbols, but to someone who does not know that ! is one
symbol, might count it as two, because of the dot symbol, and the line symbol. So to someone who
does not know that might represent 4. Let’s begin by looking at this relationship in a historical
context with the Mayan number system.
2 Mayan Number System
The work in this section is based on information from [6] and [7]. Mayan numerals have a connection
between the form they take, and the meaning, or number of objects they represent. A table of the
first 20 Mayan numerals is shown in Figure 2.
There is a clear correlation between the first 4 numerals, •, ••, • • •, • • •• and their meaning.
However when we reach 5,
, we begin to lose the direct relationship between form and meaning.
At this point, we should define each symbol, a dot represents one, a line represents five, and a
3
Figure 2: This table shows the first 20 numerals of the Mayan number system.
shell represents empty space. It has been suggested that grains or pebbles were used as counters,
represented by the dot, and a short stick or bean pod were counters represented by the line. Unlike
our number system, the Mayan number system was a base 20, or vigesimal system. Their number
system was based on their calendar system, which was a modified base twenty system. The Mayans
wrote their numbers in a positional number system. We also use a positional number system. The
major difference is that the Mayans wrote their numbers vertically, with the 1’s place value at the
bottom and we will call this register one. Above that was the 20’s place in register two, 400’s above
that in register three, 8,000’s in register four, and so on. The number 241, 083 would be written as
seen in Figure 3.
Figure 3: This table shows the positional method used to construct Mayan numerals.
2.1 Mayan Addition
In order to add using Mayan numerals, simply combine symbols that are in the same register. An
important rule to remember is that five dots equals one line. An example of simple addition can
be seen in Figure 4.
Similar to our operation of addition, sometimes it is necessary to carry. In Mayan, it is necessary
4
Figure 4: This table shows the addition of 7 plus 11.
to carry whenever the sum of a given register reaches 20. When this occurs, four bars in a given
register are traded for one dot in the register above it. An example of carrying is shown in Figure 5.
Figure 5: This table shows the addition of 8 plus 14 which utilizes carrying.
2.2 Mayan Subtraction
Similarly, to subtract in Mayan, take the difference of the symbols of the same register. A simple
example can be seen in Figure 6.
Figure 6: This table shows the subtraction of 8 from 18.
However, sometimes in order to subtract it is necessary to borrow. Borrowing entails trading
one dot from a given register, for four bars in the register beneath it, and then subtracting as usual.
An example of subtracting using borrowing is shown in Figure 7, including the intermediate step
for clarity.
2.3 Mayan Multiplication
It is widely believed that the Mayans did not use multiplication or division, but instead probably
would have just repeatedly used addition or subtraction, to get the same results. Although the
Mayans did not multiply it is possible to multiply in the Mayan number system without translating
it into our number system first. The basic rules of multiplication are a dot times a dot equals a dot,
5
Figure 7: This table shows the subtraction of 14 from 48 utilizing borrowing.
a bar times a dot equals a bar, and a bar times a bar equals a bar and a dot in the next highest
register.
A simple example problem of 6 × 7 is shown in Figure 8. To demonstrate each step of the
multiplication, the problem can be broken into four subproducts, which are then summed to determine the product. However, it should be noted that the operation of multiplication should be
done continuously, with pebbles for instance to keep a running tally, instead of summing individual
subproducts to reach the final product.
Figure 8: This table shows the multiplication of 6 times 7.
However, when trying to multiply two numbers that are larger than 19, we have to take into
consideration the register of each numeral, in order to determine what register the product goes
in. For this, we will call the first number the multiplier, and the second number the multiplicand.
The magnitude of the multiplier will be denoted as n, and the magnitude of the multiplicand will
be denoted as m. So for example with a dot in register 1 in the multiplier, the magnitude, n would
be 1. We will now modify the general multiplication rules so that they take register into account.
A dot in the nth register times a dot in the mth register equals a dot in the (n + m − 1) register.
Furthermore a line in the nth register times a dot in the mth register equals a line in the (n+m−1)
6
register. Lastly, a line in the nth register times a line in the mth register equals a dot in the (n + m)
register, and a line in the (n + m − 1) register. An example of a more complex multiplication, 27
times 132, which implements these rules, can be seen in Figure 9.
Figure 9: This table shows the multiplication of 27 times 132.
When comparing multiplication of Mayan numerals, to multiplication with Hindu-Arabic numerals, it seems that with a good understanding of the rules, it would be much easier to multiply
in Mayan. This is because there are only the three rules stated above that a person would need to
know in order to multiply in Mayan. In Hindu-Arabic multiplication on the other hand there are
many times tables. Now, some times tables are easy, like zero times anything is zero, and anything,
let’s call it x, times one is x. After that though, a person must know that two times two is four,
and six times seven is forty-two, and so on. Clearly there are many more rules a person must know
in order to multiply in Hindu-Arabic numerals.
2.4 Mayan Division
Similar to multiplication, there is no evidence to support that the Mayans used the operation of
division, but it is possible to divide using the Mayan number system. The process is comparable
7
to our Arabic long division. The general directions begin with determining how many times the
divisor goes into the dividend. Then the result is multiplied by the divisor. That product is
then subtracted from the dividend, and if the remainder is larger than the divisor, the remainder
becomes the new dividend, and the process is repeated until the remainder is less than the divisor.
To divide in the Mayan number system it is imperative to think of it as reverse multiplication. To
show the rule of division in detail, we will examine a difficult problem, 490,372 divided by 2,149.
To begin the Mayan long division notation, we write a rotated L shape, seen in Figure 10 with
the dividend, 490372, under the L, and the divisor, 2149, outside the L.
Figure 10: This image shows the process for setting up a long division problem.
From there, the first step is to determine what the highest register of the quotient will be.
For this problem, thinking in backward multiplication we see that a dot or a bar in the third,
fourth, or fifth register of the quotient times the divisor, would yield a number greater than the
dividend. Therefore, the highest register of the quotient must be the second. We see that a bar in
the second register times the divisor, is smaller than the dividend, so we subtract the product from
the dividend. We write the bar in the second register above the L, and we will call it a subquotient.
Once we have finished all the division we will add the subquotients to get the quotient. The
subquotient times the divisor, is called a subproduct, and is written to the right of the dividend
under the L as seen in Figure 11.
We then subtract the subproduct from the dividend, and write the difference to the right of the
subproduct as seen in Figure 12. From here, we can see that another bar in the second register
times the divisor is smaller than the remainder, so we subtract that product. This step is shown in
8
Figure 11: This image shows the first step in the Mayan long division process.
Figure 12: This image shows the second step in the Mayan long division process.
Figure 13. Now we can see that we cannot have another bar in the second register, but that there
could be a dot in the second register of the quotient. We subtract the product of this dot times
the divisor from the remainder as seen in Figure 14.
Now it is clear that there cannot be any more dots in the second register, so we move down to
the first register. If we put a bar in the first register times the divisor, the product will be less than
the remainder, so we subtract it. This subtraction is seen in Figure 15.
The remainder at this point is not big enough to subtract another bar-divisor product, but
we see that a dot in the first register times the divisor goes into the remainder. We subtract
this product, and clearly another dot-divisor product goes into the remainder, so we subtract that
product. One more dot-divisor product can go into the remainder, so we subtract that product
9
Figure 13: This image shows the third step in the Mayan long division process.
Figure 14: This image shows the fourth step in the Mayan long division process.
too. These last three steps can be seen in Figure 16.
Finally we see that the remainder is smaller than the divisor, and so we have all of our subquotients. Adding these subquotients together will yield the final quotient seen in Figure 17 plus the
remainder in brackets.
Clearly there are many similarities between Mayan arithmetic and Arabic arithmetic. We can
also look at the similarities found in the Babylonian number system.
3 Babylonian Number System
The work in this section comes from information in [1], [3], and [8]. The Babylonian number system
is a base 60 system, or sexagesimal system. The Babylonians used two symbols to create their first
10
Figure 15: This image shows the fifth step in the Mayan long division process.
Figure 16: This image shows the final steps in the Mayan long division process.
59 numbers. However, their number system also has hints of a base ten system. This is because
the first 59 numbers were constructed of a symbol for the units, and a symbol for the tens. Like
the Mayan number system, there is also a connection between the form of Babylonian numerals,
and their meaning. So Babylonian numerals are countable, since 1 is represented by a tree,
two is represented by two trees,
,a
, and so on. The first 59 Babylonian numerals are depicted in
Figure 18.
Much like the Arabic number system that we utilize today the Babylonians wrote their numbers
horizontally. In their positional system, the rightmost number would represent the units up to 59,
the position to the left of that represents 60 times n, where n is a number between 1 and 59, and the
number to the left of that is 602 times n, etc. To write Babylonian numbers using Arabic numerals
11
Figure 17: This image shows the final solution to our long division problem.
Figure 18: This chart depicts the first 60 Babylonian numerals.
we can utilize the notation where numerals are separated by commas. For example, 2,4,34, 11
represents the sexagesimal number 2 ∗ 603 + 4 ∗ 602 + 34 ∗ 601 + 11 ∗ 600 , or 448,451 in Arabic
numerals. The Babylonian numeral for 228,451 is shown in Figure 19.
Figure 19: The graphic above is Mayan numeral for 448,451.
However, in constructing different numbers, the Babylonians ran into some problems. For
example, how to differentiate between the number 1 and the number 60, when both are represented
by the same symbol and the only difference is the placement. How could the Babylonians show
that the
symbol for 60, was not the rightmost number, but in the second place? Similarly, the
12
Babylonians had difficulty when distinguishing between for example 61, and 2. 61 is constructed
by putting a
in the 60s place, and a
in the units place, whereas 2 is constructed by putting
in the units. To address this problem, Babylonian scribes tried to put additional space between
characters. This method however left it up to the reader to determine in what place the leftmost
symbol was occurring. For example the reader could interpret
as 3,601, or 216,001. It was
around 300BC that Babylonian mathematicians developed a zero to represent the lack of units of
a certain order. They developed the two symbols shown in Figure 20 to put in the blank spaces.
or
Figure 20: These two symbols are both representations of Babylonian zero.
Using these symbols, 3,601 and 216,001 would be represented by the numerals seen in Figure 21.
and
Figure 21: The numeral for 3,601 is shown on the left and 216,001 is on the right.
However, it must be said that neither of the symbols for zero, were ever allowed to stand alone.
This zero is only used as a placeholder, it cannot precede another number, and it cannot stand
alone. These symbols for zero were designed to differentiate between numerals in different place
values.
4 Zero
The work in this section comes primarily from [8]. It was around 2300 years ago that the Babylonians were the first to use zero as a placeholder. While this zero is useful, it had no numerical
value. Around 326BC, Alexander the Great conquered ancient Babylon, and continued on to India,
bringing the Babylonian concept of zero with him. Since the people of India saw Shiva, one of their
major deities, as nothingness or the ultimate void, they embraced zero. Indian mathematicians
gave zero its place on the number line, its power beyond place holding. They did this by thinking
13
about the idea that 2-1=1 and 2-3=-1, and 2-2=0, so 0 must go between 1 and -1 on the number
line.
In Europe however, zero was feared. Medieval scholars believed that God was omnipotent, and
that God can do anything, that He is the ultimate goodness and therefore, nothing is evil, the void
is evil, zero is evil. Europeans also feared zero, because it challenged the basic rules of arithmetic.
A number added to itself is another number,1+1=2, 2+2=4, and so on, except in the case of zero,
because 0+0=0. Zero also violated the Axiom of Archimedes, which states that if you add a number
to itself enough times, it will be larger than any other number in magnitude. However, zero never
gets bigger. Adding zero to another number also refuses to make that number any bigger. There
are similar problems with subtraction. Subtracting zero from a number does not change it.
Zero also causes problems for the operations of multiplication and division. Without zero,
multiplication can be thought of as a stretching of the number line. Multiplication by 2 stretches
the number line by a factor of two, so that 1 is now 2, 2 is now 4, -1 is now -2, and -2 is now
negative 4. Multiplying by a faction, on the other hand can be viewed as shrinking the number
line. Figure 22 illustrates these two ideas.
Figure 22: This image shows the number line when multiplied by 2 and 1/2.
However multiplication by zero crushes the number line into a single point, because any number
times zero is still zero. Without zero, division is the inverse to multiplication, that is (2 × 3)/3 = 2,
and (4 × 5)/5 = 4. Following this line of thought, it would make sense that any number times zero
divided by zero should send every number back to its place on the number line. So we would expect
that (1 × 0)/0) = 1 and (2 × 0)/0 = 2, but 1 × 0 = 0 and 2 × 0 = 0. Therefore (1 × 0)/0) = 0/0 and
(2 × 0)/0 = 0/0, which would mean that 0/0 = 1, 2, 3, 4, ... This is why we do not divide by zero.
The Greeks, who did not believe in nothing or the void, also did not believe in zero. Yet, they
14
saw the usefulness of zero, and so Greek astronomers would translate their numbers into Babylonian
notation, do their calculations, and then convert back to Greek notation. They did this so the only
recorded numbers would be in Greek, because they did not want people to find out about zero,
since it went against their philosophical beliefs. Their disbelief in zero also meant that they could
not take limits, because if there is no zero, there is nothing for the limit to approach. This disbelief
in zero, held back Greek mathematics, and it was not until 1202 in Fibonacci’s Liber Abaci that
zero was finally introduced to Europe.
However, not everyone avoided expressions containing 0/0. L’Hôpital was interested in investigating how to determine the value of a function that approaches 0/0 at a point. He did this by
creating l’Hôpital’s rule, which states that the value of a fraction is equivalent to the derivative
of the numerator divided by the derivative of the denominator. To understand further, let’s look
at an example. When x=0, the expression x/ sin(x) = 0/0 as x=0, and sin(0) = 0. However, if
we apply l’Hôpital’s rule we see this expression becomes 1/ cos(x), by taking the derivative of the
numerator divided by the derivative of the denominator, and so when x=0, we have 1/ cos(0), or
1/1=1. Unfortunately, l’Hôpital’s rule looks at 0/0 by using methods that build upon 0/0 to begin
with, making it a circular argument. Eventually the concept of limits was developed by Cauchy
and Weierstrass. Limits allow mathematicians to work with zeros and infinity, by taking limits of
partial sums, and since partial sums are finite, they can be divided without any fear of obtaining
0/0. This idea of limits will be important in constructing the real numbers.
5 Constructing the Real Number Line
This section is based on information provided in chapters 1 and 2 of [9]. Now that we have some
understanding of the integers, we will summarize key properties of the rational number system,
since we want these properties to hold in the real number line as well.
5.1 Rational Numbers
A rational number is a number that takes the form p/q where p and q are both integers and q is
not zero. Rational numbers p/q and p’/q’ represent the same number if and only if pq’=p’q. There
is a unique irreducible way to represent every rational number where q is positive and as small as
15
possible. When working with rationals, p/q, we will assume that p/q is in reduced form with q
positive. Addition of rational numbers is defined by
p p!
pq ! + p! q
+ ! =
q q
qq !
multiplication is defined by
p × p!
p p!
× ! =
q q
q × q!
and division is defined by
p p!
p × q!
÷ ! =
q q
q × p!
Since the rational numbers are a field under addition and multiplication, we have the following
properties:
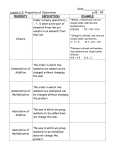
• Addition and multiplication are commutative and associative.
a + b = b + a, (a + b) + c = a + (b + c), a × b = b × a, (a × b) × c = a × (b × c)
• Multiplication distributes over addition
a × (b + c) = a × b + a × c
• 0 is the additive identity
0+a=a
• 1 is the multiplicative identity
1×a=a
• Every rational number has an additive inverse
a + (−a) = 0
• Every non-zero rational has a multiplicative inverse
a × (1/a) = 1
A rational number, p/q, is positive if p and q are positive, and is negative if p is negative and
q is positive. Every rational number is either positive, negative, or zero. Another property of the
rational number line is the triangle inequality, where |a − b| ≥| a| −| b|. We also have the Axiom
16
of Archimedes which states that for every positive rational number a > 0 there exists an integer
n such that a > 1/n. Following from this we have that for every positive rational number a > 0,
there is an integer n such that 0 < a < n. Lastly, we have that between any two distinct rational
numbers there is an infinite number of other rational numbers.
5.2 Real Numbers from Cauchy Sequences
As we construct the real numbers, we want it to contain, the rational numbers, and have similar
operations, and properties. We want the real numbers to be an ordered field, that is have all of the
properties of a field as listed above, and properties of order such that if a ≤ b then a + c ≤ b + c;
and if 0 ≤ a and 0 ≤ b, then 0 ≤ ab. We could construct the real numbers by using infinite decimal
expansions, where every number would be of the form ±N.a1 a2 a3 ... where N is a nonnegative
integer, and ai is an integer from 0 to 9. To see this we can look at some examples: 1 = 1.000000...,
−1/11 = −0.090909..., as these two numbers are rational they have repeating decimals, but we
√
√
can also write 2 as an infinite decimal expansion, where 2 = 1.414213..., which does not have
repetition. However, as infinite decimal expansions are infinite, we would prefer not to use them
to construct the reals.
Another way to construct the real numbers is to look at the limits of Cauchy sequences. The
Cauchy convergence criterion, is that for all natural numbers n there exists a natural number m,
which depends on n, such that |xj − xk | < 1/n for all j ≥ m and k ≥ m. So a Cauchy sequence
is a sequence that meets this convergence criterion. The limits of Cauchy sequences will include
every real number, because every real number has an infinite decimal expansion. Each expansion
can be written as ±N , ±N.a1 , ±N.a1 a2 , ... which is a Cauchy sequence. We say that two Cauchy
sequences are equivalent if they have the same limit. Furthermore, sequences A and B belong to
the same equivalence class if and only if A is equivalent to B. We will call all the Cauchy sequences
x1 , x2 , ... of rational numbers, C. The set of equivalence classes of elements of C will be noted at R,
or the real number system.
5.3 The Reals as an Ordered Field
Now that we have constructed the real numbers, we want to make sure that they have the same
basic properties of arithmetic and order as the rational number system. So, if we let x1 , x2 , ... and
17
y1 , y2 , ... be Cauchy sequences of rationals, then x1 + y1 , x2 + y2 , ... is also a Cauchy sequence of
rationals. From there, we have that the equivalence class of the Cauchy sequence x1 + y1 , x2 + y2 , ...
, where x1 , x2 , ... represents x and y1 , y2 , ... represents y, is the real number x+y. Similarly, if we
let, x1 , x2 , ... and y1 , y2 , ... be Cauchy sequences of rationals, then x1 y1 , x2 y2 ,... is also a Cauchy
sequence of rationals. The real number x × y is the equivalence class of the Cauchy sequence x1 y1 ,
x2 y2 , ... where x1 , x2 , ... represents x and y1 , y2 , ... represents x and y respectively.
The real numbers form a field under the operations of addition and multiplication with the
following properties:
• Addition is commutative
x+y =y+x
• Addition is associative
(x + y) + z = x + (y + z)
• 0 is the additive identity
0+x=x
• Every element, x has an additive inverse, –x
x + (−x) = 0
• Multiplication is commutative
x×y =y×x
• Multiplication is associative
(x × y) × z = x × (y × z)
• 1 is the multiplicative identity
1×x=x
• Every element, x, except 0 has a multiplicative inverse, x−1
x−1 × x = 1
• Multiplication distributes over addition
x × (y + z) = x × y + x × z
18
We also have that if x is a real number besides 0, then there exists a natural number N such that
for every Cauchy sequence x1 , x2 , ... in the equivalence class of x, there exists an m such that
|xi | ≥ 1/N for all i ≥ m. This will help us in trying to establish order among the reals. In ordering
the real numbers, we would like to have real numbers either be positive, negative or zero like the
rational numbers. We will call a real number x positive if there exists a natural number N and
m such that xj ≥ 1/N for all j ≥ m, where x1 , x2 , ... represent x. A real number is considered
negative, x < 0, if -x is positive. Now, that we have positive and negative reals, we can order them
using inequalities: x > y means that x-y is positive; x ≥ y means that either x > y or x = y;
|x| < y means that y-x and y+x are both positive, and so on. Furthermore, |x| is x if x > 0, |x| is
-x if x < 0, and |0| = 0. Finally, like the triangle inequality of the rational numbers, we also have
a triangle inequality for the real numbers, which states that |x + y| ≤| x| + |y| for real numbers x
and y.
5.4 Dedekind Cuts
Real numbers can also be constructed by using Dedekind Cuts. A real number, x, creates a division
of the rational numbers into two sets, those less than x, and those greater than x. If x is a rational
number, then it is grouped with the set of rationals greater than x. We want to associate each real
number x, with Lx , the set of all rational numbers less than x. A Dedekind cut is a set of rational
numbers, L that satisfies the following properties:
• L is not empty
• L is not all the rationals
• If r is in L, and q < r then q is in L
• If r is in L, there exists an s in L with s > r
Any subset L of rationals with these properties must be Lx for some real number x. So we have
that the Dedekind real numbers system is the set of all Dedekind cuts. Let’s look at an example
as shown through the Dedekind cut which represents the square root of 2.
We let L be the set of all negative rational numbers, and the positive rational numbers that
satisfy r2 < 2. As L contains all negative rational numbers, clearly L is not empty, and satisfies the
19
first condition. As L contains only positive rational numbers where r2 < 2, obviously all positive
rationals with r2 > 2 are not included in L, so L is not all rationals, which satisfies the second
condition. To check the third condition, we assume r is in L, and q < r. If r < 0, then q < 0,
so q is in L because L contains all negative rational numbers. However, if r > 0 and q > 0, then
q 2 < r2 < 2 as q < r and so q is in L. For the last condition, we assume r is in L. If r < 0, let s = 1,
then s is in L as 12 < 2. If r > 0 and r2 < 2, then let s = r + 1/n, so s > r. However, as 1/n can
be infinitely small, we have r2 < s2 = (r + 1/n)2 < 2 by the Axiom of Archimedes. As L satisfies
the four properties, L is a Dedekind cut.
6 Constructible Numbers
Another way that we can obtain numbers, is through geometric construction. Information from this
section comes from ideas presented in [2]. We call a real number α constructible, if we can construct
a line segment of length |α| in a finite number of steps using only an unmarked straightedge, a
compass, and a unit of length 1. From plane geometry is is clear to see that if α and β, where
β '= 0 , are constructible numbers, then so are α + β, α − β, α × β, and α/β. These geometric
constructions are pictured below.
The first is the construction of a + b as seen in Figure 23. We construct a + b from given lengths
a and b, by using a compass centered at point x on a line to construct an arc at length b. Then
starting from the point y where arc b crosses the line, we use the compass again to construct an
arc at length a. We call the point where arc a crosses the line, point z. Then the length of the line
segment xz is a + b.
The construction of a − b can be seen in Figure 24. To construct a − b from given lengths a
and b, we begin by centering a compass at point x, and creating an arc at length a. We call point
where arc a crosses the line, point z. Starting from point x again, we construct an arc at length b.
The point where arc b crosses the line is called point y. Now, we have the length of yz is a − b.
In order to construct a × b or ab, as seen in Figure 25, we need given lengths of a, b, and unit
length 1, where a and b are constructible. First we start at point l and construct an arc at length 1.
We call the point where this arc crosses the line point m. Beginning at point l again, we construct
an arc at length b. We call the point where this arc crossed the line point n. Then beginning at
20
Figure 23: This image shows the construction of a+b.
Figure 24: This image shows the construction of a-b.
point l we use the compass to construct an arc at length a on some new line that passes through
point l. The point where this arc crosses the new line is called point o. Next, we connect points
m and o. Then we create a line parallel to mo that goes through point n. The point where this
line crosses the line through points l and o, is called point p. We will say that line segment lp is
of length x. Then since triangles lmo and lnp are similar, we have that
b
1
=
x
a.
When we cross
multiply we get that ab = x. Therefore, the line segment lp is of length ab.
Similarly, to construct a ÷ b or ab , as seen in Figure 26, we will need given lengths of a, b, and
unit length 1, where b '= 0, and a and b are constructible. First we start at point c and construct
an arc at length 1. We call the point where this arc crosses the line point d. Beginning at point c
again, we construct an arc at length b. We call the point where this arc crossed the line point e.
Then beginning at point c we use the compass to construct an arc at length a on some new line
21
Figure 25: This image shows the construction of a×b.
that passes through point c. The point where this arc crosses the new line is called point g. Next,
we connect points e and g. Then we create a line parallel to eg that goes through point d. The
point where this line crosses the line through points c and g, is called point f . We will say that line
segment cf is of length x. Then since triangles cdf and ceg are similar, we have that
b
1
= xa . When
we cross multiply we get that bx = a, or x = ab . Therefore, the line segment cf is of length ab .
√
Lastly, in order to construct c, as seen in Figure 27, we begin by using a compass to create the
semicircle wzy. Beginning at point w, we will construct an arc at length 1, and will call the point
where the arc crosses the base of the semicircle point x. We will call the length of line segment xy,
length c. We then construct a line perpendicular to the base of the semicircle, that passes through
point x. The point where this line intersect the semicircle is called point z. We will say that the
22
Figure 26: This image shows the construction of a÷b.
line segment xz has length d. Then as triangles wxz and xzy are similar, we have that dc = d1 . By
√
cross multiplying we get that c = d2 , and then d = c. Therefore, the line segment xz is of length
√
c.
7 A Non-Numerical Approach
This section is based on ideas found in [5]. We can also think about numbers by using sets. We
begin by noting that there is only one empty set {}, and it exists. As the empty set is unique,
there is only one set, whose only element is the empty set: {{}}. Furthermore, there is only one set
whose elements are the empty set, and the set whose only members are the empty set: {{},{{}}}.
Now, let A be a set, and A’ be the successor of A, where A’ consists of the members of A and a
new member that is A itself. An example is shown below.
23
Figure 27: This image shows the construction of
√
c.
E={}
E’ = {}’ ={{}}
E” = {{}}’ = {{},{{}}}
E”’ = {{}, {{}}}’ = {{}, {{}}, {{}, {{}}}}
..
.
Clearly none of these sets are equal to each other. Each, set in this sequence becomes a reference
set for a corresponding number, or there is a number that refers to each set. Looking back at our
example, the empty set is the reference for 0, E’ is the reference for 1, E” is the reference for 2,
and so on. That is, each reference set: E, E’, and E” is the physical representation of a number:
0,1, and 2 respectively. Once again, with this representation of numbers we can see a connection
between the form of the number and its meaning. Here we have zero represented by the empty set,
the set of no elements, and one represented by E’ or {{}} which is a set with one element, and two
represented by E” = {{},{{}}}, which is a set containing two elements. Obviously, this method of
looking at number assigns the numeral its meaning, by the number of elements in its reference set.
24
8 Roots of Hindu-Arabic Numerals
Information from this section follows from work presented in [4]. The Hindu-Arabic numerals have
their origins in the Brahmi system of writing from India around the mid third century BCE. Then
around the 8th century, during the Islamic invasions into northern India, the Muslims were first
exposed to these digits. At this time the Muslims also conquered much of the Mediterranean. So
these numerals were next seen in Spain about a century later, followed by their appearance in Italy
still later, and eventually the rest of Europe. Figure 28 shows the progression of the Hindu-Arabic
numerals.
Figure 28: This graphic shows the progression of Hindu Arabic numerals from A History of Mathematics An Introduction page 234.
It is clear that the form of the first three numerals from the Brahmi system of writing, have a
connection to their meaning. It is also interesting to note that in the Brahmi system, the numerals
for six and seven appear quite similar to the numerals we use for six and seven in Hindu-Arabic
system today. Furthermore in the Brahmi system, there is no numeral for zero. We first see
25
the numeral for zero in the Indian number system. However, in the Indian system we lose the
connection between form and meaning for the first three numerals. Also, in the Indian system,
there is a similarity in the numerals two, three, seven, and nine to our Hindu-Arabic numerals.
Another interesting point to note is that in the Indian numeral system the numeral for five looks
very much like our numeral for four.
It is at this point in history that there is a split, and the Indian numeral system gives way to
three different systems: the West Arabic (gubar) system, the Sanskrit-Devanagari (Indian) system,
and the East Arabic system, the last of which is still used in Turkey today. Of these three systems,
the West Arabic system appears most like the Hindu-Arabic system we use, as the numerals one,
two, three, six, seven, eight, and nine are almost identical to the numerals we use today. However,
it seems that the numeral for zero we use today likely comes from the Sanskrit-Devanagari system.
It is clear that the numerals used in the 16th century, are practically the same numerals we use
today in the Hindu Arabic system.
9 Conclusion
At the beginning of the year, when I was looking over a list of possible project topics, the idea
”What are Numbers?” immediately stood out to me. It’s not a question that we’re asked very
often, or ever, unless you know some little kids. As I thought about it and tried to formulate an
answer, I realized how hard it is to articulate my own ideas of what a number is. Over the past
year, I have explored a numerous paths that lead to the heart of the question: how did ancient
societies view numbers, how do we formally construct the real number line, what numbers can
be physically constructed geometrically, how can we look at numbers without using numbers, and
where do we get the numerals we use today. Even after all that, it’s still a challenge to try to answer
the question, ”What is a number?” However, throughout the entire process I always felt like I was
an adventurer; I learned so many new things and I thought about numbers in ways I never have
before. If I were to do more research in this area in the future, I would really like to look at how
numbers are taught to children in school. I’d also like to take a look at imaginary, complex, and
transcendental numbers, because I have not worked with them much throughout my math career.
26
References
[1] J.
O’Connor,
E.
Robertson,
Babylonian
Mathematics,
http://www-groups.dcs.st-
and.ac.uk/ history/Indexes/Babylonians.html
[2] J. Gallian, Contemporary Abstract Algebra, Brooks/Cole, Cengage Learning, Belmont, CA,
2010
[3] L. Geller, Zero as a Placeholder, http://www.und.edu/instruct/lgeller/zeroph.html
[4] V. Katz, A History of Mathematics An Introduction, Addison-Wesley, Boston, 2009
[5] L. Kauffman, What is a Number?, preprint, http://homepages.math.uic.edu/ kauffman/NUM.html
[6] J. Lambert, B. Ownbey-McLaughlin, C. McLaughlin, Maya Arithmetic, American Scientist,
Vol. 68, No. 3(May-June, 1980), pp. 249-255
[7] G. Salyers, The Number System of the Mayas, Mathematics Magazine, Vol. 28, No. 1 (Sep. Oct., 1954), pp 44- 48
[8] C. Seife, Zero: The Biography of a Dangerous Idea, Penguin Books, New York , 2000
[9] R. Strichartz The Way of Analysis, Jones and Bartlett Publishers, Boston, 1995
27