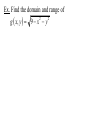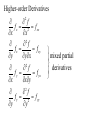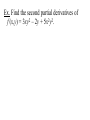Download 205 13.1 and 13.3

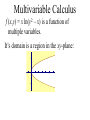
Multivariable Calculus
f (x,y) = x ln(y2 – x) is a function of
multiple variables.
It’s domain is a region in the xy-plane:
Multivariable Calculus
f (x,y) = x ln(y2 – x) is a function of
multiple variables.
It’s domain is a region in the xy-plane:
2
5
-2
Multivariable Calculus
f (x,y) = x ln(y2 – x) is a function of
multiple variables.
It’s domain is a region in the xy-plane:
2
5
-2
f (3,2) = 3 ln (22 – 3) = 3 ln (1) = 0
Ex. Find the domain of f  x, y  
x  y 1
x 1
Ex. Find the domain and range of
2
2
g  x, y   9  x  y
Ex. Sketch the graph of f (x,y) = 6 – 3x – 2y.
This is a linear function of two variables.
Ex. Sketch the graph of g  x, y   9  x  y
2
2
Ex. Find the domain and range of
f (x,y) = 4x2 + y2 and identify the graph.
Ex.
lim
 x , y 1,2
 x y
2
3
 x y  3x  2 y 
3
2
This is a polynomial function of two variables.
When trying to sketch multivariable
functions, it can convenient to consider level
curves (contour lines). These are 2-D
representations of all points where f has a
certain value.
This is what you do when drawing a
topographical map.
Ex. Sketch the level curves of f  x, y   9  x 2  y 2
for k = 0, 1, 2, and 3.
Ex. Sketch some level curves of f (x,y) = 4x2 + y2
A function like T(x,y,z) could represent the
temperature at any point in the room.
Ex. Find the domain of f (x,y,z) = ln(z – y).
Ex. Identify the level curves of
f (x,y,z) = x2 + y2 + z2
Partial Derivatives
A partial derivative of a function with
multiple variables is the derivative with
respect to one variable, treating other
variables as constants.
If z = f (x,y), then

z
wrt x: f x  x, y  
f  x, y   z x 
x
x

z
f  x, y   z y 
wrt y: f y  x, y  
y
y
Ex. Let f  x, y   xe , find fx and fy and
evaluate them at (1,ln 2).
x2 y
zx and zy are the slopes in the x- and ydirection
Ex. Find the slopes in the x- and y-direction
2
1 2
of the surface f  x, y   2 x  y  258 at
1
 2 ,1,2
Ex. For f (x,y) = x2 – xy + y2 – 5x + y, find all values
of x and y such that fx and fy are zero simultaneously.
Ex. Let f (x,y,z) = xy + yz2 + xz, find all
partial derivatives.
Higher-order Derivatives

 f
f x  2  f xx
x
x
2

 f
fx 
 f xy
y
yx
2

 f
fy 
 f yx
x
xy
2

 f
f y  2  f yy
y
y
2

 mixed partial

derivatives


Ex. Find the second partial derivatives of
f (x,y) = 3xy2 – 2y + 5x2y2.
fxy = fyx
Ex. Let f (x,y) = yex + x ln y, find fxyy, fxxy, and
fxyx.
A partial differential equation can be used
to express certain physical laws.
u u
 2 0
2
x
y
2
2
This is Laplace’s equation. The solutions,
called harmonic equations, play a role in
problems of heat conduction, fluid flow,
and electrical potential.
Ex. Show that u(x,y) = exsin y is a solution to
Laplace’s equation.
Another PDE is called the wave equation:
2
2
u
2  u
a
2
2
t
x
Solutions can be used to describe the motion
of waves such as tidal, sound, light, or
vibration.
The function u(x,t) = sin(x – at) is a solution.