Midterm Review
... 40. What are the focus and directrix of the parabola with equation 41. Identify the focus and the directrix of the graph of 42. Identify the focus and the directrix of the graph of ____ 43. What is an equation of a parabola with focus ...
... 40. What are the focus and directrix of the parabola with equation 41. Identify the focus and the directrix of the graph of 42. Identify the focus and the directrix of the graph of ____ 43. What is an equation of a parabola with focus ...
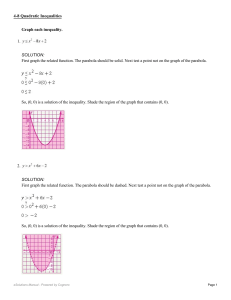
Graph each inequality. 1. SOLUTION: First graph the related function
... Since a negative value for time has no meaning, discard the negative solution. So, the ball hits the ground in about 24.61 seconds. The ball will be inside the goal when 0 < t < 3.11 or 20.89 < t ≤ 24.61. ...
... Since a negative value for time has no meaning, discard the negative solution. So, the ball hits the ground in about 24.61 seconds. The ball will be inside the goal when 0 < t < 3.11 or 20.89 < t ≤ 24.61. ...
screen pdf: 1.8 Mo, 186 p. - IMJ-PRG
... Thrinacia, stretching far in all ways, were filled with their multitude. Again, when the yellow and the dappled bulls were gathered into one herd they stood in such a manner that their number, beginning from one, grew slowly greater till it completed a triangular figure, there being no bulls of othe ...
... Thrinacia, stretching far in all ways, were filled with their multitude. Again, when the yellow and the dappled bulls were gathered into one herd they stood in such a manner that their number, beginning from one, grew slowly greater till it completed a triangular figure, there being no bulls of othe ...
HOMEWORK 1 – SOLUTION
... 6. If vector a has magnitude kak = 3 and vector b has magnitude kbk = 4, what is the largest possible magnitude for the vector a + b? What is the smallest possible magnitude for the vector a + b? What will be the magnitude of a + b if a and b are perpendicular? Answer. The largest magnitude of a + b ...
... 6. If vector a has magnitude kak = 3 and vector b has magnitude kbk = 4, what is the largest possible magnitude for the vector a + b? What is the smallest possible magnitude for the vector a + b? What will be the magnitude of a + b if a and b are perpendicular? Answer. The largest magnitude of a + b ...
limits and derivatives conditions for the existence of a limit
... The gradient of a line is constant and does not change at different values of x . As the derivative represents the gradient to a curve, the derivative of a linear expressions will result in a constant (numeric) value. The gradient to a curve modelled by a non linear equation changes, and is dependen ...
... The gradient of a line is constant and does not change at different values of x . As the derivative represents the gradient to a curve, the derivative of a linear expressions will result in a constant (numeric) value. The gradient to a curve modelled by a non linear equation changes, and is dependen ...
Do Now 2/8/07
... 28) one solution 10) one solution 30) one solution 36) No, there are infinitely many solutions ...
... 28) one solution 10) one solution 30) one solution 36) No, there are infinitely many solutions ...
solving equations and inequalities
... Solution: Let x represent the number of minutes of use. Peg’s phone costs 25 + 0.25x. Larry’s phone costs 35 + 0.20x. We want Peg’s cost to exceed Larry’s: P > L or P – L > 0. If we subtract 35 + 0.20x from 25 + 0.25x, the result is –10 + 0.05x. Replacing P – L with –10 + 0.05x, we have –10 + 0.05x ...
... Solution: Let x represent the number of minutes of use. Peg’s phone costs 25 + 0.25x. Larry’s phone costs 35 + 0.20x. We want Peg’s cost to exceed Larry’s: P > L or P – L > 0. If we subtract 35 + 0.20x from 25 + 0.25x, the result is –10 + 0.05x. Replacing P – L with –10 + 0.05x, we have –10 + 0.05x ...
Math 55b Lecture Notes Contents
... spaces. In a general topological space there is not a good enough notion of “distance” to make this definition work. Question 2.2. Show that a sequence which converges is automatically Cauchy. (Draw a picture.) Now we can define the following. Definition 2.3. A metric space M is complete if every Ca ...
... spaces. In a general topological space there is not a good enough notion of “distance” to make this definition work. Question 2.2. Show that a sequence which converges is automatically Cauchy. (Draw a picture.) Now we can define the following. Definition 2.3. A metric space M is complete if every Ca ...
convex functions on symmetric spaces, side lengths of polygons and
... on the Schubert calculus whereas their solution set depends only on the Weyl group. This is due to possible redundancies. In rank one, i.e., when X has strictly negative sectional curvature, we have ∆euc ∼ = R+ 0 and the stability inequalities are just the ordinary triangle inequalities. In Section ...
... on the Schubert calculus whereas their solution set depends only on the Weyl group. This is due to possible redundancies. In rank one, i.e., when X has strictly negative sectional curvature, we have ∆euc ∼ = R+ 0 and the stability inequalities are just the ordinary triangle inequalities. In Section ...
On the Brahmagupta–Fermat–Pell Equation x2 dy2 = ±1 - IMJ-PRG
... As a function of the integer k, we have B + N = 4Ak with A = 3 · 11 · 29 · 4657 squarefree. Hence k = AU 2 with U an integer. On the other side if T + X is a triangular number (= m(m + 1)/2), then ...
... As a function of the integer k, we have B + N = 4Ak with A = 3 · 11 · 29 · 4657 squarefree. Hence k = AU 2 with U an integer. On the other side if T + X is a triangular number (= m(m + 1)/2), then ...
Pdf - Text of NPTEL IIT Video Lectures
... avoid writing too much. Let me give you a notation eta of some T, where T is the rectangle. Let us say it is essentially the contour integral along the boundary of T f of z d z for any rectangular region T. So, that is the notation I will use, okay. So, let us start with a picture. So, here is the r ...
... avoid writing too much. Let me give you a notation eta of some T, where T is the rectangle. Let us say it is essentially the contour integral along the boundary of T f of z d z for any rectangular region T. So, that is the notation I will use, okay. So, let us start with a picture. So, here is the r ...
educative commentary on jee 2014 advanced mathematics papers
... same as the JEE in two tiers which prevailed for a few years. It was hoped that now that the number of candidates appearing for the JEE (Advanced) is manageable enough to permit evaluation by humans, the classic practice of requiring the candidates to give justifications for their answers would be ...
... same as the JEE in two tiers which prevailed for a few years. It was hoped that now that the number of candidates appearing for the JEE (Advanced) is manageable enough to permit evaluation by humans, the classic practice of requiring the candidates to give justifications for their answers would be ...
DEFINITE INTEGRALS
... shaded region in Fig.27.3. Now the problem is to find the area of the shaded region. In order to solve this problem, we consider three special cases of f (x) as rectangular region , triangular region and trapezoidal region. The area of these regions = base × average height In general for any functio ...
... shaded region in Fig.27.3. Now the problem is to find the area of the shaded region. In order to solve this problem, we consider three special cases of f (x) as rectangular region , triangular region and trapezoidal region. The area of these regions = base × average height In general for any functio ...
(1,1)fyy - KSU Web Home
... value of y, there are no critical points for this function. 13. For the function f (x, y) = x sin (y) , we have fx = sin (y) fy = x cos (y) . The critical points occur at values (x, y) such that sin (y) = 0 x cos (y) = 0. In the above system of equations, if x = 0, then any value of y such that sin ...
... value of y, there are no critical points for this function. 13. For the function f (x, y) = x sin (y) , we have fx = sin (y) fy = x cos (y) . The critical points occur at values (x, y) such that sin (y) = 0 x cos (y) = 0. In the above system of equations, if x = 0, then any value of y such that sin ...
Variational Iterative Method Applied to Variational Problems with
... Type 2: For the second case, the beginning and end points (or only one of them) can move freely on given curves y x , y x . In this case, a function y x is required, which emanates at some x x0 from the curve y x and terminates for some x x1 on the curve y x a ...
... Type 2: For the second case, the beginning and end points (or only one of them) can move freely on given curves y x , y x . In this case, a function y x is required, which emanates at some x x0 from the curve y x and terminates for some x x1 on the curve y x a ...
Lecture 16
... we have ignored n=0 solution because it gives rise to logarithm in radial coordinate which diverges at origin. Thus the general solution for the potential is where K is a constant. Further, the constant D must be zero otherwise the potential would diverge at . Let us now apply the boundary condition ...
... we have ignored n=0 solution because it gives rise to logarithm in radial coordinate which diverges at origin. Thus the general solution for the potential is where K is a constant. Further, the constant D must be zero otherwise the potential would diverge at . Let us now apply the boundary condition ...
Integral Calculus - Exercises
... Therefore, the desired function is f (x) = 14 x4 + x2 + 2x − 54 . 9. It is estimated that t years from now the population of a certain lakeside community will be changing at the rate of 0.6t2 + 0.2t + 0.5 thousand people per year. Environmentalists have found that the level of pollution in the lake ...
... Therefore, the desired function is f (x) = 14 x4 + x2 + 2x − 54 . 9. It is estimated that t years from now the population of a certain lakeside community will be changing at the rate of 0.6t2 + 0.2t + 0.5 thousand people per year. Environmentalists have found that the level of pollution in the lake ...
Algebra 1 Foundations, pg 202 Focus Question
... solutions. You will use the Addition Property of Inequality and the Subtraction Property of Inequality to produce equivalent inequalities. To check the solution of an inequality, you need to check at least two values. First, determine if the endpoint is a solution of the related equation. Then, choo ...
... solutions. You will use the Addition Property of Inequality and the Subtraction Property of Inequality to produce equivalent inequalities. To check the solution of an inequality, you need to check at least two values. First, determine if the endpoint is a solution of the related equation. Then, choo ...
(a) f(x) - Portal UniMAP
... • The first derivative test can also be used to determine the critical points. • However, it is used only if the second derivative test fails. • Three steps are required in the first derivative test. 1. Find f' (x). 2. Let f' (x) = 0 and solve for critical values, c. 3. Select points in the neighbou ...
... • The first derivative test can also be used to determine the critical points. • However, it is used only if the second derivative test fails. • Three steps are required in the first derivative test. 1. Find f' (x). 2. Let f' (x) = 0 and solve for critical values, c. 3. Select points in the neighbou ...
Hypoelliptic non homogeneous diffusions
... C ∞ diffeomorphism of Rd . Here of course Πx denotes the projection operator from R ⊗ Rd onto Rd . Note that the standard proof, lying on Kolmogorov continuity theorem, allows to choose such a version for each u, but non necessarily for all u simultaneously. In particular if one wants to use the pat ...
... C ∞ diffeomorphism of Rd . Here of course Πx denotes the projection operator from R ⊗ Rd onto Rd . Note that the standard proof, lying on Kolmogorov continuity theorem, allows to choose such a version for each u, but non necessarily for all u simultaneously. In particular if one wants to use the pat ...
Antiderivatives - John Abbott College
... In a derivative problem, a function f (x) is given and you find the derivative f ′ (x) using the formulas and rules of derivatives shown in a previous tutorial. In an antiderivative problem, the derivative f ′ (x) is given and you find a function f (x) using the formulas of antiderivatives shown lat ...
... In a derivative problem, a function f (x) is given and you find the derivative f ′ (x) using the formulas and rules of derivatives shown in a previous tutorial. In an antiderivative problem, the derivative f ′ (x) is given and you find a function f (x) using the formulas of antiderivatives shown lat ...
At x - Year11IB
... Differentiation is a technique for finding the gradient of any point on a curved line. Finding the gradient of a straight line is easy because the gradient is the same at every part of the line. y y2 ...
... Differentiation is a technique for finding the gradient of any point on a curved line. Finding the gradient of a straight line is easy because the gradient is the same at every part of the line. y y2 ...
The mathematics of PDEs and the wave equation
... D2 = ∇2 . Good luck solving this one.5 The operator D is called the Dirac operator; finding particular Dirac operators is a major intellectual achievement of modern mathematics and physics. The Atiyah-Singer index theorem is a deep result connecting the Dirac operator with the geometry of manifolds. ...
... D2 = ∇2 . Good luck solving this one.5 The operator D is called the Dirac operator; finding particular Dirac operators is a major intellectual achievement of modern mathematics and physics. The Atiyah-Singer index theorem is a deep result connecting the Dirac operator with the geometry of manifolds. ...
Sample pages 1 PDF
... In the historical problems set forth here we have shown how functionals of the form given by Eq. (2.2) may enter directly into problems of interest. Actually the extremization of such functionals or their more generalized forms is equivalent to solving certain corresponding differential equations, a ...
... In the historical problems set forth here we have shown how functionals of the form given by Eq. (2.2) may enter directly into problems of interest. Actually the extremization of such functionals or their more generalized forms is equivalent to solving certain corresponding differential equations, a ...
Solutions to Practice Problems for Test 2
... 2. Find the general solution of the given DE 2y 000 − 4y 00 − 2y 0 + 4y = 0. Solution: The characteristic equation is 2r3 − 4r2 − 2r + 4 = 2(r2 − 1)(r − 2) = 0 whose roots are −1, 1 and 2. The solutions of the DE are et , e−t , e2t . 3. Let the linear differential operator L be defined by L[y] = a4 ...
... 2. Find the general solution of the given DE 2y 000 − 4y 00 − 2y 0 + 4y = 0. Solution: The characteristic equation is 2r3 − 4r2 − 2r + 4 = 2(r2 − 1)(r − 2) = 0 whose roots are −1, 1 and 2. The solutions of the DE are et , e−t , e2t . 3. Let the linear differential operator L be defined by L[y] = a4 ...