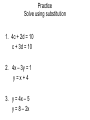* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download PPadua-Douglas,E. CNM 2011-11-02 8847
Survey
Document related concepts
Transcript
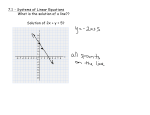
October 31, 2011 At the end of today, you will be able to: Solve linear equations by graphing. Determine what each system indicates about their solutions. HW 3.1&3.2 Pg. 113 #13-17, 25,27 y odds, Pg. 120 #13-17 odds Graph y = 2x – 3 5 -3 1: Start at___________ 2 2: (up or down)____steps 1 3: right______step 4: Plot the point, and continue -5 steps #1-4 to find more points. 5: Draw the line that goes through the points. -5 6: Label the line. x 5 Use a straight edge, graph paper, and two different colored pencils to graph the following: 1. Graph two of the lines on the same graph: y = x – 1 and y = -x – 3 2. Graph: 1 y x 3 and 2 3. Graph: y = -2x + 4 and 1 y x 1 2 4 y x4 2 What do the graphs of System of Equations tell you? Intersecting Lines Exactly one solution Consistent and independent Parallel Lines No solution Inconsistent Same Line Infinitely many solutions Consistent and dependent A solution of the system of equations is the ordered pair where the two lines intersect. What point did the two lines in #1 intersect? So, (-1, -2) is the solution for the system: y = x – 1 and y = -x – 3 Example 1: Solve the system by *If the equations graphing. 2x + y = -7 x–y=1 are in standard form, find the xy-intercepts. 2x + y = -6 x–y=1 x-int (-3, 0) x-int (1, 0) y-int (0, -6) y-int (0,-1) Example 2: Graph the system and describe it as a consistent and independent, consistent and dependent, or inconsistent. 6x + 8y = -16 3 y x 2 4 Use Slope Intercept Form or find the x-yintercepts How does a system of equations work? Figure out the ages for: , if, , + = 16 =5 + − =1 Example 1: Solve using Substitution x + 2y = 8 1 Step 1: x y 18 Isolate one of 2 the variables. Step 2: Substitute the value of the variable in the 2nd equation. Step 3: Simplify and solve for the variable. x = 8 – 2y 1 (8 2y) y 18 2 4 y y 18 4 – 2y = 18 -4 -4 -2y = 14 y = -7 Wait! You’re not done, what does x equal? Example 1 continued: x + 2y = 8 1 x y 18 2 Step 4: Substitute again into one of the equations to solve for the other variable. Since y = -7, x + 2(-7) = 8 x - 14 = 8 +14 +14 x = 22 The solution to the system is x = 22 and y = -7, or (22, -7) Practice Solve using substitution 1. 4c + 2d = 10 c + 3d = 10 2. 4x – 3y = 1 y=x+4 3. y = 4x – 5 y = 8 – 2x