Download 5.4 Systems_Elimination using multiplication

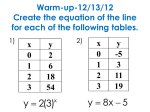
5.4 Elimination Using
Multiplication
Objective: Each student will understand if addition and
subtraction does not eliminate a variable – how they can
use multiplication to solve real world problems.
Academic Standard:2.4d Solve systems of equations.
Algebra 1
Notes:
When should I use the method of
elimination using multiplication?
How do I use the method of
elimination using multiplication?
What do I do next?
If the coefficients of one of the
variables are not additive inverses or not
the same.
Multiply each term of one equation by
the same number, or, multiply both
equations by different numbers in order
to have one of the variables have
coefficients that are additive inverses of
each other or the same number.
Use the elimination method using
addition and subtraction to find the
solution.
Example 1: Use elimination to solve the system
3x + 4y = 6
5x + 2y = -4
3x + 4y = 6
-2(5x + 2y = -4)
3x + 4y = 6
-10x - 4y = 8
-7x
= 14
x = -2
No coefficients are
additive inverses or
the same
Multiply the second
equation by -2
3x + 4y = 6
3(-2) + 4y = 6
Substitute x = -2 in
to one of the
original equations
-6 + 4y = 6
Add 6 to both sides
4y = 12
Add the two
equations
Divide both sides
by 4
y=3
Solution: (-2, 3)
Divide both sides
by -7
Practice 1: Use elimination to solve the system
a) 5x + 3y = 8
x+y=2
b) 3x + 4y = -25
2x – 3y = 6
Practice 2: Use elimination to solve the system
a)
2x – 5y = 11
3x + 2y = 26
b) 4x + 6y = 26
2x + 3y = 13
Example 2: The admission fee at a small fair is $1.50 for
children and $4.00 for adults. On a certain day, 2200
people enter the fair and $5050 is collected. How many
children and how many adults attended?
Define variables: a = adult tickets c = children’s tickets
Write a verbal expression for each equation
children tickets
1.50 times children tickets
plus
plus
adult tickets
4.00 times adult tickets is
Write an algebraic expression for each equation
Solve using elimination
is
c + a = 2200
1.5c + 4a = 5050
2200 tickets
$5050
Assignment
Pg 275 1-4, 8-16 even, 37-42