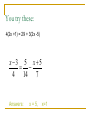Download Lesson 1.2A Notes

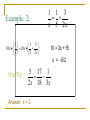
Warm-up
1.
Determine the x-intercept (s) and y-intercept from the
graph below.
Homework:
Determine what this viewing rectangle illustrates.
pg. 104, (1-45 odds)
2. [-20, 40, 5] by [-10, 30, 2]
Problems 10-14 must
3. Solve this equation: 4x + 5 = 29
show checking your
answer.
Answers:

1. x-intercepts = (3,0) and (-7,0)
y-intercept = (0,21)
it’s a reflection

2. The x window’s min is at -20, max at 40
increasing in increments of 5. The y window’s
min is at -10, max at 30 increasing in increments
of 2.

3. x = 6
Announcements:
Ch 1 Learning Goal: The student will be able to
understand functions by solving and graphing
all types of equations and inequalities.
Today’s Objective: Be able to solve a
rational equations with variables
Lesson 1.2A Linear Equations and
Rational Equations

A linear equation in one variable x is an
equation that can be written in the form of
ax + b = 0,
where a and b are real numbers
and a  0.
Steps for Solving a Linear Equation:
1. Simplify the algebraic expression on each
side by removing grouping symbols and
combining like terms.
2. Collect all the variable terms on one side
and all the numbers, or constant terms, on
the other side.
3.
Isolate the variable and solve.
4. Check the proposed solution in
the original equation.
Example 1: Solving a Linear Equation
Involving Fractions
x  2 x 1

2
4
3
Given.
 x  2 x 1 
12 

  2  12
3 
 4
Find LCD.
3(x+2)-4(x-1)=24
Solve by Distributive
Property and combine
like terms.
3x +6-4x+4 = 24
-x = 14
x = -14
Solve and check.
You try these:
4(2x +1) = 29 + 3(2x -5)
x3 5 x5
 
4
14
7
Answers:
x = 5,
x=1
Example 2:
1 1 3
 
x 5 2x
1
1 3 
10 x     10 x    
 x
 5 2x 
10 = 2x +15
x = -5/2
You Try:
5 17 1
 
2 x 18 3 x
Answer: x = 3
Example 3: Solving Rational Equations
Write problem.
Objective – try to clear
fractions.
Multiply both sides by
x
3
( x  3) 
 ( x  3)  (
 9)
(x-3) to cancel it out on the left
x 3
x 3
side
x
3
Distribute the (x-3) on the right
( x  3)   ( x  3)  ( )  ( x  3)  9 side
x3
x3
Cross out the (x-3) to get rid of
x
3
them in denominators
x
3

9
x 3 x 3
( x  3) 
x3
 ( x  3)  (
x3
)  9( x  3)
Example Continued
X = 3 + 9(x-3)
X = 3 + 9x – 27
X = 9x – 24
Simplify
Distribute the 9
Subtract 3 and -27
Subtract 9x from both sides
-8x = -24
X=3
Divide by -8.
Unfortunately not a solution
because of the excluded
values. The solution is an
empty set, 0 .
You Try!
x
2
2


x2
x2
3
Write problem
x
2
2
3( x  2) 
 3( x  2)  (
 )
x 2
x 2 3
x
2
2
3( x  2) 
 3( x  2)( )  3( x  2)( )
x 2
x 2
3
x
2
2
3( x  2) 
 3( x  2)( )  ( )3( x  2)
x 2
x 2 3
3 x  6  ( 2 x  4)
Multiply both sides by
3(x-2)
Distribute the 3(x-2) to the
right side
Cancel out any 3(x-2)
Multiply
3x  2  2 x  4
Distribute the negative
3x  6  2 x  4
Solve for x.
3 x  10  2 x
Not a solution because of the
excluded values.
The solution is an empty set, 0
5 x  10
x  2
Summary: What is a rational equation?
Give an example of this type of
equation.



Homework: WS1.1
pg. 104, (1-45 odd)
Problems 10-14 must show
checking your answer.