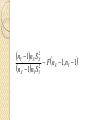Download PowerPoint

Examples and Multivariate
Testing
Lecture XXV

Example 9.6.1 (mean of a binomial
distribution) Assume that we want to
know whether a coin toss is biased based
on a sample of ten tosses.
◦ Our null hypothesis is that the coin is fair (H0:
p=1/2) versus an alternative hypothesis that
the coin toss is biased towards heads
(H1:p>1/2).
◦ Assume that you tossed the coin ten times
and observed eight heads. What is the
probability of drawing eight heads from ten
tosses of a fair coin?
10  10
10  9
10  8
0
1
2
Pn  8    p 1  p     p 1  p     p 1  p 
10 
9
8
If p=1/2, P [n≥8]=.054688. Thus, we reject H0
at a confidence level of .10 and fail to reject
H0 at a .05 confidence level.
◦ Moving to the Likelihood ratio test:
 p  .5
.5 1  .5
 8
 .1455  
2
.8 1  .8
 pˆ MLE  .8
2
8
◦ Given that
 2 ln   ~ 
2
1
We reject the hypothesis of a fair coin toss at
a .05 confidence level. (-2 ln()=3.854 and
the critical region for a chi-squared
distribution at one degree of freedom is 3.84.

Example 9.6.2. Suppose the heights of
male Stanford students is distributed
N(m,s2) with a known variance of .16.
◦ Assume that we want to test whether the
mean of this distribution is 5.8 against the
hypothesis that the mean of the distribution is
6. What is the test statistic for a 5 percent
level of confidence and a 10 percent level of
confidence?
◦ Under the null hypothesis
.16 

X ~ N  5.8,

10 

◦ The test statistic then becomes
6  5.8
Z
 1.58 ~ N 0,1
.1265
Given that P[Z≥1.58]=.0571, we have the
same decisions as above, namely that we
reject the hypothesis at a confidence level of
.10 and fail to reject the hypothesis at a
confidence level of .05.

Example 9.6.3 (mean of normal with
variance unknown) Assume the same
scenario as above, but that the variance is
unknown, but estimated to be .16. The
test then becomes:
X  6 ~ t
.16
10
9
◦ The computed statistic becomes
P[t9>1.58]=.074.

Example 9.6.7 (differences in variances).
In lecture XIX, we discussed the chisquared distribution as a distribution of
the sample variance.
◦ Theorem 5.4.1: Let X1, X2,…Xn be a random
sample from a N (m,s2) distribution, and let
1 n
X  i 1 X i
n
and
1
n
2


S 
X

X

i
n  1 i 1
2
 X and S2 are independent random variables


X ~ N m ,s
2
n
 (N-1)S2/s2 has a chi-squared distribution with n-1
degrees of freedom.

Given the distribution of the sample
variance, we may want to compare two
sample variances:
n X S X2
~
2
n X 1
and
nY SY2
~
2
nY 1
s
s
 Dividing the first by the second and
correcting for degrees of freedom yields
2
X
2
Y
nY  1nX S
nX  1nY S
2
X
2
Y
~ F nX  1, nY  1
Testing Hypothesis about Vectors

Extending the test results beyond the test
of single parameters, we now want to test
H0: q=q0 against H1: q≠q0 where q is a k x
1 vector of parameters.
◦ We begin by assuming that
qˆ ~ N q , S 
where S is known
◦ First, assuming that k=2, we have
 qˆ1 
  q1   s 11 s 12  
  ~ N   , 



 q   s
qˆ 
s
22  
  2   12
 2
◦ A simple test of the null hypothesis, assuming
that the parameters are uncorrelated would
then be
2
2
qˆ1  q1
qˆ2  q 2
R:

c
s 11
s 22

 


Building on this concept, assume that we
can design a matrix A such that ASA’=I.
This theorem relies on the eigenvalues of
the matrix.
◦ Specifically, the eigenvalues of the matrix l are
defined by the solution of the equation
det(S-I l)=0.
 These values are real if the S matrix is symmetric
and positive if the S matrix is positive definite. In
addition, if the matrix is positive definite, there are k
distinct eigenvalues.
 Associated with each eigenvalue is an eigenvector, u,
defined by u (S-I l)=0.
◦ Carrying the eigenvector multiplication
through implies ASA=0 where A is a
matrix of eigenvectors and  is a diagonal
matrix of eigenvalues. By construction, the
eigenvectors are orthogonal so that AA’=I.
Thus, ASA’=. The above decomposition is
guaranteed by the diagonal nature of .

Assuming that this matrix is constant, we
can change the hypothesis to H0: Aq=Aq0
with
Aqˆ ~ N  Aq , I 
This transformation implies





ˆ
ˆ
ˆ
 A  q  q  A  q  q  q  q AA qˆ  q

ˆ
  q  q  S  qˆ  q   c
 ˆ
ˆ
R : Aq  Aq Aq  Aq  c
1

Note that the likelihood ratio test for this
scenario becomes:
 1 ˆ

 1 ˆ
exp   q  q S q  q 
2



 1 ˆ

 1 ˆ
max
exp

q

q
S
q

q
MLE
MLE


qˆ MLE
 2














ˆq  q S1 qˆ  q ~ 2
0
0
k

A primary problem in the construction of
these statistics is the assumption that we
know the variance matrix. If we assume
that we know the variance matrix to a
scalar (S=s2Q where Q is known and s2
is unknown), the test becomes



ˆq  q  Q 1 qˆ  q
0
0
s
2
 c

Using the traditional chi-squared result
W
s

2
~
2
M
Dividing the first expression by the
second yields



ˆq  q  Q 1 qˆ  q
0
0
W
M
 ~ F K, M 