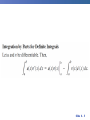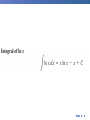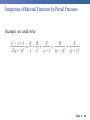Download Document

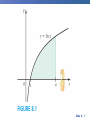
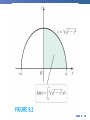
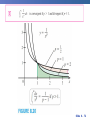
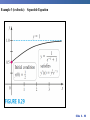
Chapter 8
Integration Techniques
8.1
Integration by Parts
Slide 8 - 3
.
Integrate by parts: Practice!
http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/intbypartsdirectory/IntByParts.html
Slide 8 - 4
Slide 8 - 5
Slide 8 - 6
Slide 8 - 7
8.2
Trigonometric Integrals
Slide 8 - 9
Slide 8 - 10
Slide 8 - 11
Slide 8 - 12
8.3
Trigonometric Substitutions
Slide 8 - 14
Trigonometric Substitution

In finding the area of a circle or an ellipse, an integral of the
form
dx arises, where a > 0.

If it were
the substitution
u = a2 – x2 would be effective but, as it stands,
dx is more difficult.
Slide 8 - 15
Trigonometric Substitution

If we change the variable from x to  by the substitution
x = a sin , then the identity 1 – sin2 = cos2 allows us to get rid of
the root sign because
Slide 8 - 16
Example 1

Evaluate
Solution:
Let x = 3 sin , where – /2     /2. Then dx = 3 cos  d
and


(Note that cos   0 because – /2     /2.)
Slide 8 - 17
Example 1 – Solution
cont’
By Inverse Substitution we get:
Slide 8 - 18
Example 1 – Solution

Since this is an indefinite integral, we must return to thecont’
original variable x. This can be done either by using
trigonometric identities to express cot  in terms of
sin  = x/3 or by drawing a diagram, as in Figure 1,
where  is interpreted as an angle of a right triangle.
sin  =
Figure 1
Slide 8 - 19
Example 1 – Solution
cont’


Since sin  = x/3, we label the opposite side and the
hypotenuse as having lengths x and 3.
Then the Pythagorean Theorem gives the length of the
adjacent side as
so we can simply read the
value of cot  from the figure:
Slide 8 - 20
Example 1 – Solution
cont’

Since sin  = x/3, we have  = sin–1(x/3) and so
Slide 8 - 21
Slide 8 - 22
Slide 8 - 23
Example 2

Find

Solution:
Let x = 2 tan , – /2 <  <  /2. Then dx = 2 sec2 d
and
=
= 2| sec  |
= 2 sec 
Slide 8 - 24
Example 2 – Solution
cont’
Thus we have
To evaluate this trigonometric integral we put everything in
terms of sin  and cos  :
Slide 8 - 25
Example 2 – Solution
cont’
=
Therefore, making the substitution u = sin , we have
Slide 8 - 26
Example 2 – Solution
cont’
Slide 8 - 27
Example 2 – Solution
cont’
We use the figure below to determine that csc  =
so
and
Figure 3
Slide 8 - 28
Example 3
Find
Solution:
First we note that (4x2 + 9)3/2 =
is appropriate.
so trigonometric substitution
Although
is not quite one of the expressions in the table
of trigonometric substitutions, it becomes one of them if we make the
preliminary substitution u = 2x.
Slide 8 - 29
Example 3 – Solution
cont’
When we combine this with the tangent substitution, we have x =
which gives
and
When x = 0, tan  = 0, so  = 0; when x =
tan  =
so = /3.
Slide 8 - 30
Example 3 – Solution
cont’

Now we substitute u = cos  so that du = –sin  d.
When  = 0, u = 1; when  =  /3, u =
Slide 8 - 31
Example 3 – Solution
cont’
Therefore
Slide 8 - 32
8.4
Partial Fractions
Slide 8 - 34
Integration of Rational Functions by Partial Fractions
To see how the method of partial fractions works in
general, let’s consider a rational function
where P and Q are polynomials.
It’s possible to express f as a sum of simpler fractions
provided that the degree of P is less than the degree of Q.
Such a rational function is called proper.
Slide 8 - 35
Integration of Rational Functions by Partial Fractions

If f is improper, that is, deg(P)  deg(Q), then we must
take the preliminary step of dividing Q into P (by long
division) until a remainder R (x) is obtained such that
deg(R) < deg(Q).
where S and R are also polynomials.
Slide 8 - 36
Example 1
Find
Solution:
Since the degree of the numerator is greater than the
degree of the denominator, we first perform the long
division.
This enables us to write:
Slide 8 - 37
Integration of Rational Functions by Partial Fractions
If f(x) = R (x)/Q (x) is a proper rational function:
factor the denominator Q (x) as far as possible.
Ex: if Q (x) = x4 – 16, we could factor it as
Q (x) = (x2 – 4)(x2 + 4) = (x – 2)(x + 2)(x2 + 4)
Slide 8 - 38
Integration of Rational Functions by Partial Fractions
Next: express the proper rational function as a sum of
partial fractions of the form
or
A theorem in algebra guarantees that it is always possible
to do this.
Four cases can occur.
Slide 8 - 39
Integration of Rational Functions by Partial Fractions
Case I The denominator Q (x) is a product of distinct linear
factors.
This means that we can write
Q (x) = (a1x + b1)(a2x + b2) . . . (akx + bk)
where no factor is repeated (and no factor is a constant
multiple of another).
Slide 8 - 40
Integration of Rational Functions by Partial Fractions
In this case the partial fraction theorem states that there
exist constants A1, A2, . . . , Ak such that
These constants can be determined as in the next
example.
Slide 8 - 41
Example 2
Evaluate
Solution:
Since the degree of the numerator is less than the degree
of the denominator, we don’t need to divide.
We factor the denominator as
2x3 + 3x2 – 2x = x(2x2 + 3x – 2)
= x(2x – 1)(x + 2)
Slide 8 - 42
Example 2 – Solution
Since the denominator has three distinct linear factors, the
partial fraction decomposition of the integrand has the form
To determine the values of A, B, and C, we multiply both
sides of this equation by the product of the denominators,
x(2x – 1)(x + 2), obtaining
x2 + 2x – 1 = A(2x – 1)(x + 2) + Bx(x + 2) + Cx(2x – 1)
Slide 8 - 43
Example 2 – Solution
cont’
Expanding the right side and writing it in the standard form
for polynomials, we get
x2 + 2x – 1 = (2A + B + 2C)x2 + (3A + 2B – C)x – 2A
These polynomials are identical, so their coefficients must
be equal. The coefficient of x2 on the right side, 2A + B +
2C, must equal the coefficient of x2 on the left side—
namely, 1.
Likewise, the coefficients of x are equal and the constant
terms are equal.
Slide 8 - 44
Example 2 – Solution
cont’
This gives the following system of equations for A, B, and
C:
2A + B + 2C = 1
3A + 2B – C = 2
–2A = –1

Solving, we get, A =
B=
and C =
and so
Slide 8 - 45
Example 2 – Solution
cont’
In integrating the middle term we have made the mental
substitution u = 2x – 1, which gives du = 2 dx and
dx = du.
Slide 8 - 46

Note:
We can use an alternative method to find the coefficients
A, B and C. We can choose values of x that simplify the
equation:
x2 + 2x – 1 = A(2x – 1)(x + 2) + Bx(x + 2) + Cx(2x – 1)
If we put x = 0, then the second and third terms on the right
side vanish and the equation then becomes –2A = –1, or A
= .
Likewise, x = gives 5B/4 =
so B = and C =
and x = –2 gives 10C = –1,
Slide 8 - 47
Integration of Rational Functions by Partial Fractions
Case II: Q (x) is a product of linear factors, some of which
are repeated.
Suppose the first linear factor (a1x + b1) is repeated r times;
that is, (a1x + b1)r occurs in the factorization of Q (x). Then
instead of the single term A1/(a1x + b1) in the equation:
we use
Slide 8 - 48
Integration of Rational Functions by Partial Fractions
Example, we could write
Slide 8 - 49
Example 3
Find
Solution:
The first step is to divide. The result of long division is
Slide 8 - 50
Example 3 – Solution
cont’
The second step is to factor the denominator
Q (x) = x3 – x2 – x + 1.
Since Q (1) = 0, we know that x – 1 is a factor and we
obtain
x3 – x2 – x + 1 = (x – 1)(x2 – 1)
= (x – 1)(x – 1)(x + 1)
= (x – 1)2(x + 1)
Slide 8 - 51
Example 3 – Solution
cont’
Since the linear factor x – 1 occurs twice, the partial
fraction decomposition is
Multiplying by the least common denominator,
(x – 1)2(x + 1), we get
4x = A (x – 1)(x + 1) + B (x + 1) + C (x – 1)2
Slide 8 - 52
Example 3 – Solution
cont’
= (A + C)x2 + (B – 2C)x + (–A + B + C)
Now we equate coefficients:
A+C=0
B – 2C = 4
–A + B + C = 0
Slide 8 - 53
Example 3 – Solution
cont’
Solving, we obtain A = 1, B = 2, and C = –1, so
Slide 8 - 54
Integration of Rational Functions by Partial Fractions
Case III: Q (x) contains irreducible quadratic factors, none
of which is repeated.
If Q (x) has the factor ax2 + bx + c, where b2 – 4ac < 0,
then, in addition to the partial fractions, the expression for
R (x)/Q (x) will have a term of the form
where A and B are constants to be determined.
Slide 8 - 55
Integration of Rational Functions by Partial Fractions

Example:
f (x) = x/[(x – 2)(x2 + 1)(x2 + 4)] has the partial fraction decomposition:

Any term of the form:
can be integrated by
completing the square (if necessary) and using the formula
Slide 8 - 56
Example 4
Evaluate
Solution:
Since the degree of the numerator is not less than the
degree of the denominator, we first divide and obtain
Slide 8 - 57
Example 4 – Solution
cont’
Notice that the quadratic 4x2 – 4x + 3 is irreducible because
its discriminant is b2 – 4ac = –32 < 0. This means it can’t be
factored, so we don’t need to use the partial fraction
technique.
To integrate the given function we complete the square in
the denominator:
4x2 – 4x + 3 = (2x – 1)2 + 2
This suggests that we make the substitution u = 2x – 1.
Slide 8 - 58
Example 4 – Solution
cont’
Then du = 2 dx and x = (u + 1), so
Slide 8 - 59
Example 4 – Solution
cont’
Slide 8 - 60

Note:
Example 6 illustrates the general procedure for
integrating a partial fraction of the form
where b2 – 4ac < 0
We complete the square in the denominator and then make
a substitution that brings the integral into the form
Then the first integral is a logarithm and the second is
expressed in terms of
Slide 8 - 61
Integration of Rational Functions by Partial Fractions
Case IV: Q (x) contains a repeated irreducible quadratic
factor.
If Q (x) has the factor (ax2 + bx + c)r, where b2 – 4ac < 0,
then instead of the single partial fraction
, the
sum:
occurs in the partial fraction decomposition of R (x)/Q (x).
Each of the terms can be integrated by using a substitution
or by first completing the square if necessary.
Slide 8 - 62
Example 5
Evaluate
Solution:
The form of the partial fraction decomposition is
Multiplying by x(x2 + 1)2, we have
–x3 + 2x2 – x + 1 = A(x2 +1)2 + (Bx + C)x(x2 + 1) + (Dx + E)x
Slide 8 - 63
Example 5 – Solution
cont’
= A(x4 + 2x2 +1) + B(x4 + x2) + C(x3 + x) + Dx2 + Ex
= (A + B)x4 + Cx3 + (2A + B + D)x2 + (C + E)x + A
If we equate coefficients, we get the system
A+B=0
C = –1
2A + B + D = 2
C + E = –1
A=1
which has the solution A = 1, B = –1, C = –1, D = 1 and E = 0.
Slide 8 - 64
Example 5 – Solution
cont’
Thus
Slide 8 - 65
Slide 8 - 66
8.7
Improper Integrals
Type 1: Infinite Intervals
Slide 8 - 68
Slide 8 - 69
Examples:
Slide 8 - 70
Practice Example:
Determine whether the integral
is convergent or divergent.
Solution:
According to part (a) of Definition 1, we have

The limit does not exist as a finite number and so the
Improper integral
is divergent.
Slide 8 - 71
Slide 8 - 72
Slide 8 - 73
Examples:
Slide 8 - 74
Type 2: Discontinuous Integrands

Suppose that f is a positive continuous function defined on a
finite interval [a, b) but has a vertical asymptote at b.

Let S be the unbounded region under the graph of f and above
the x-axis between a and b. (For Type 1 integrals, the regions
extended indefinitely in a horizontal direction. Here the region
is infinite in a vertical direction.)

The area of the part of S between a and t is
Figure 7
Slide 8 - 75
Type 2: Discontinuous Integrands
Slide 8 - 76
Practice Example:
Find
 Solution:
We note first that the given integral is improper
because
has the vertical
asymptote x = 2.


Since the infinite discontinuity occurs at the left
endpoint of [2, 5], we use part (b) of Definition 3:
Slide 8 - 77
Example – Solution
cont’d

Thus the given improper integral is convergent and,
since the integrand is positive, we can interpret the
value of the integral as the area of the shaded region.
Figure 10
Slide 8 - 78
Gabriel’s Horn:
Slide 8 - 79
8.8
Introduction to Differential Equations
Ordinary Differential Equations
Definition
A differential equation is an equation containing an unknown
function and its derivatives.
Examples:.1.
dy
 2x  3
dx
2
d
y
dy
2.
3
 ay  0
2
dx
dx
4
3
3. d y  dy 
    6y  3
3
dx
 dx 
y is the dependent variable and x is independent
variable.
Slide 8 - 81
Partial Differential Equation
Examples:
1.
 2u  2u
 2 0
2
x
y
u is the dependent variable and x and y are independent
variables.
2.
 4u  4u
 4 0
4
x
t
3.
 2 u  2 u u
 2 
2
t
x
t
u is dependent variable and x and t are independent variables
Slide 8 - 82
Order of a Differential Equation
The order of the differential equation is the order of the highest
derivative in the differential equation.
Differential Equation
ORDER
dy
 2x  3
dx
1
d2y
dy
 3  9y  0
2
dx
dx
2
4
d y  dy 
    6y  3
3
dx
 dx 
3
3
Slide 8 - 83
Degree of Differential Equation
The degree of a differential equation is the power of the highest
order derivative term in the differential equation.
Differential Equation
d2y
dy
 3  ay  0
2
dx
dx
Degree
1
4
d 3 y  dy 
    6y  3
3
dx
 dx 
3
 d 2 y   dy 
 2      3  0
 dx   dx 
1
5
3
Slide 8 - 84
Linear Differential Equation
A differential equation is linear, if:
1. The dependent variable and its derivatives
are of degree one,
2. The coefficient of any term does not contain
the dependent variable, y.
d2y
dy

3
 9 y  0.
2
dx
dx
Examples:
d2y
dy

3
 9 y  0.
dx
dx 2
is linear.
is non-linear because 3rd term contains y
4
d 3 y  dy 
    6y  3
dx 3  dx 
is non-linear because the 2nd term is not of degree one.
Slide 8 - 85
3.
d2y
dy
3
x

y

x
dx
dx 2
2
is non-linear because in the 2nd term the coefficient contains y.
4.
dy
 sin y
dx
is non–linear because the coefficient on the left hand side contains y
Slide 8 - 86
Solving Differential Equations
87
Slide 8 - 87
First Order Differential Equations
The most general first order differential equation can be written as:
There is no general formula for the solution. We will look at two types of
these and how to solve them:
Linear Equations
Separable Equations
Slide 8 - 88
Linear Differential Equations: Integrating Factor Method
If not already in the following form, re-express the equation in the
form:
(1)
where both p(t) and g(t) are continuous functions
Assume there is a function,
, called an integrating factor.
Multiply each term in (1) by
. This will give:
Slide 8 - 89
NOW: assume that whatever
is, it will satisfy the following :
Do not worry about how we can find a
is continuous we will find it!
that will satisfy the above. As long as p(t)
The equation becomes:
We recognize that the left side is nothing more than the following product rule:
Slide 8 - 90
The equation becomes:
integrate both sides :
Finally, the solution y(t) is:
Slide 8 - 91
What is
for any given equation ?
We started with assuming:
So:
Finally:
Slide 8 - 92
Practice Example:
Solve
with y(0) = 1.
Step1: Compare the equation with the standard form:
We identify:
and
.
Step2: Find the integrating factor
Step3: Multiplying through by the integrating factor, we get
Step4: Rewrite
as the derivative
.
.
Step5: Integrate both sides with respect to x and get
Step6: Use the initial condition to find c.
So the solution to the problem is
,
gives:
and finally:
.
Slide 8 - 93
Linear Differential Equations: Separable Equations
A separable differential equation is any differential equation that we can write in the
following form
Now rewrite the differential equation as:
Integrate both sides. Use the initial condition to find the constant of integration.
Slide 8 - 94
Practice Example:
Solve
with y(0) = 1.
Step1: Divide through by y. We get:
Step2: Integrate both sides:
Step3: Solving for y gives:
where
Step4: Use the initial condition:
to get: A = 1
So the solution to the problem is:
Slide 8 - 95
Examples from textbook:
Slide 8 - 96
Example 2 (textbook) : Initial Value Problem Drug Dosing
Slide 8 - 97
Example 3 (textbook) : Separable Equation
Slide 8 - 98
Example 4 (textbook) : Separable Equation Logistic Population Growth
Slide 8 - 99
Directional Fields: Reading assignment
(for your general Math knowledge).
Slide 8 - 100