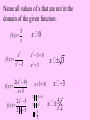Download PPT Review 1.1-1.3

REVIEW 1.1-1.3
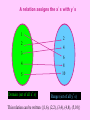
A relation is a set of ordered
pairs.
The domain is the set of all x values in the relation
domain = {-1,0,2,4,9}
These are the x values written in a set from smallest to largest
{(2,3), (-1,5), (4,-2), (9,9), (0,-6)}
These are the y values written in a set from smallest to largest
range = {-6,-2,3,5,9}
The range is the set of all y values in the relation
This is a
relation
A relation assigns the x’s with y’s
1
2
3
4
2
4
6
5
8
10
Domain (set of all x’s)
Range (set of all y’s)
This relation can be written {(1,6), (2,2), (3,4), (4,8), (5,10)}
AAfunction
function fffrom
fromset
setAAto
toset
setBBisisaarule
ruleof
ofcorrespondence
correspondence
that
thatassigns
assigns to
toeach
eachelement
element xxin
in the
theset
setAAexactly
exactly one
element
element yyin
inthe
theset
setB.
B.
1
2
3
4
5
2
4
6
8
10
Set A is the domain
What
This is a Whew!
function
did that
---it meets
oursay?
conditions
Set B is the range
Must use all the x’s
The x value can only be assigned to one y
Let’s look at another relation and decide if it is a function.
The second condition says each x can have only one y, but it CAN
be the same y as another x gets assigned to.
1
2
3
4
5
2
4
6
8
10
Set A is the domain
This is a function
---it meets our
conditions
Set B is the range
Must use all the x’s
The x value can only be assigned to one y
1
2
3
4
5
2
4
6
8
10
2 was assigned both 4 and 10
Is the relation shown above a function?
NO
Why not???
Evaluating
Functions
Remember---this tells you what
is on the right hand side---it is
not something you work. It says
that the right hand side is the
function f and it has x in it.
f  x   2 x  3x  6
2
f 2   22   32   6
2
f 2  24  32  6  8  6  6  8
So we have a function called f that has the variable x in it.
Using function notation we could then ask the following:
This means to find the function f and instead of
having an x in it, put a 2 in it. So let’s take the
Find f (2).
function above and make brackets everywhere
the x was and in its place, put in a 2.
Don’t forget order of operations---powers, then
multiplication, finally addition & subtraction
Find f (-2).
f  x   2 x  3x  6
2
f  2  2 2  3 2  6
2
f  2  24  3 2  6  8  6  6  20
This means to find the function f and instead of having an x
in it, put a -2 in it. So let’s take the function above and make
brackets everywhere the x was and in its place, put in a -2.
Don’t forget order of operations---powers, then
multiplication, finally addition & subtraction
f  x   2 x  3x  6
2
Find f (k).
f k   2k   3k   6
2
 
f k   2 k  3k   6  2k  3k  6
2
2
This means to find the function f and instead of having an x
in it, put a k in it. So let’s take the function above and make
brackets everywhere the x was and in its place, put in a k.
Don’t forget order of operations---powers, then
multiplication, finally addition & subtraction
f  x   2 x  3x  6
2
Find f (2k).
f 2k   22k   32k   6
2
 
f 2k   2 4k  32k   6  8k  6k  6
2
2
This means to find the function f and instead of having an x in
it, put a 2k in it. So let’s take the function above and make
brackets everywhere the x was and in its place, put in a 2k.
Don’t forget order of operations---powers, then
multiplication, finally addition & subtraction
Let's try a new function
Find g(1)+ g(-4).
g x   x  2 x
2
g 1  1  21  1
2
g  4   4  2 4  16  8  24
2
So g 1  g  4  1  24  23
Find the domain for the following functions:
Since no matter what value you
choose for x, you won't be dividing
f x  2x 1 by zero or square rooting a negative
number, you can use anything you
Note: There is
want so we say the answer is:
nothing wrong with
the top = 0 just means All real numbers x.

the fraction = 0
x3
g x  
x2
illegal if this
is zero
If you choose x = 2, the denominator
will be 2 – 2 = 0 which is illegal
because you can't divide by zero.
The answer then is:
All real numbers x such that x ≠ 2.
means does not equal
Let's find the domain of another one:
h x   x  4
Can't be negative so must be ≥ 0
x4 0
solve
this
x4
We have to be careful what x's we use so that the second
"illegal" of square rooting a negative doesn't happen. This
means the "stuff" under the square root must be greater
than or equal to zero (maths way of saying "not negative").
So the answer is:
All real numbers x such that x ≠ 4
Name all values of x that are not in the
domain of the given function.
5
f (x) =
x
x
f (x) = 2
x -3
2
2(x 2 - 9)
f (x) =
x +3
2x - 5
f (x) =
2 x -5
3
x¹0
x2 - 3 = 0
x =3
2
x +3= 0
2 x -5=0
2 x =5
5
x=
2
x ¹± 3
x ¹ -3
x ¹ ±5
2
Given that x is an integer, state the relation representing each of the
following by listing a set of ordered pairs. Then state whether the
relation is a function or not.
y = 5x - 7
And
0£ x£3
{(0, -7), (1, -2), (2, 3), (3, 8)}
IS THIS A FUNCTION???
YES
Given that x is an integer, state the relation representing each of the
following by listing a set of ordered pairs. Then state whether the
relation is a function or not.
y = 3x
3
And
-2 < x < 3
{(-1, 3), (0, 0), (1, 3), (2, 24)}
IS THIS A FUNCTION???
YES
Given that x is an integer, state the relation representing each of the
following by listing a set of ordered pairs. Then state whether the
relation is a function or not.
y = 4+ x
And
-8 £ x < -2
{(-8, 4), (-7, 3), (-6, 2), (-5, 1), (-4, 0), (-3, 1)}
IS THIS A FUNCTION???
YES
The sum f + g
 f  g x  f x  gx
This just says that to find the sum of two functions, add
them together. You should simplify by finding like terms.
f x   2 x  3
g x   4 x  1
2
3
f  g  2x  3  4x 1
2
3
 4x  2x  4
3
2
Combine like
terms & put in
descending
order
The difference f - g
 f  g x  f x  gx
To find the difference between two functions, subtract
the first from the second. CAUTION: Make sure you
distribute the – to each term of the second function. You
should simplify by combining like terms.
f x   2 x  3
2

g x   4 x  1
3

f  g  2x  3  4x 1
2
3
Distribute
negative
 2 x  3  4 x  1  4 x  2 x  2
2
3
3
2
The product f • g
 f  g x  f x g x
To find the product of two functions, put parenthesis
around them and multiply each term from the first
function to each term of the second function.
f x   2 x  3
g x   4 x  1
2

3


f  g  2x  3 4x 1
2
3
 8 x  2 x  12 x  3
5
2
3
FOIL
Good idea to put in
descending order
but not required.
The quotient f /g
f
f x 
 x  
g x 
g
To find the quotient of two functions, put the first one
over the second.
f x   2 x  3
2
f 2x  3
 3
g 4x 1
2
g x   4 x  1
3
Nothing more you could do
here. (If you can reduce
these you should).
The Composition Function
 f  g x  f gx
This is read “f composition g” and means to copy the f
function down but where ever you see an x, substitute in
the g function.
f x   2 x  3
2
g x   4 x  1
3
f  g  24 x  1  3
3
2
FOIL first and
then distribute
the 2
 32 x  16 x  2  3  32 x  16 x  5
6
3
6
3
g  f x  g f x
This is read “g composition f” and means to copy the g
function down but where ever you see an x, substitute in
the f function.
f x   2 x  3
g x   4 x  1
2
3
g  f  42 x  3  1
2
3
You could multiply
this out but since it’s
to the 3rd power we
won’t
Graphically, the x and y values of a
point are switched.
The point (4, 7)
has an inverse point
of (7, 4)
AND
The point (-5, 3)
has an inverse
point of (3, -5)
Graphically, the x and y values of a point are switched.
If the function y = g(x)
contains the points
10
8
6
x
0
1
2
3
4
4
y
1
2
4
8
16
2
-10
-8
-6
-4
-2
2
4
6
8
10
then its inverse, y = g-1(x),
contains the points
-2
-4
x
1
2
4
8
16
-6
y
0
1
2
3
4
-8
-10
Where is there a
line of reflection?
y = f(x)
The graph of a
function and its
inverse are
mirror images
about the line
y=x
y=x
y = f-1(x)
Find the inverse of a function :
Example 1: y = 6x - 12
Step 1: Switch x and y: x = 6y - 12
Step 2: Solve for y:
x = 6y - 12
x + 12 = 6y
x + 12
=y
6
1
x+2= y
6
Example 2:
Given the function :
y = 3x2 + 2 find the inverse:
Step 1: Switch x and y:
x = 3y2 + 2
Step 2: Solve for y:
x = 3y 2 + 2
x - 2 = 3y
2
x-2
= y2
3
x-2
=y
3
Ex: Find an inverse of y = -3x+6.
• Steps: -switch x & y
-solve for y
y = -3x+6
x = -3y+6
x-6 = -3y
x6
y
3
1
y  x2
3
Find the zero of each function.
Then graph the function.
1.) f(x) = 3x - 8
2.) f(x) = 19
3x - 8 = 0
19 = 0
3x = 8
Not True
8
x=
3
No Zero!!!
Graphing Linear Equations and
Inequalities
Linear Equations in Two Variables
y
Example
Graph 7x + y > –14
• Graph 7x + y = –14 as a
dashed line.
• Pick a point not on the
graph: (0,0)
• Test it in the original
inequality.
7(0) + 0 > –14, 0 > –14
• True, so shade the side
containing (0,0).
(0, 0)
x
Linear Equations in Two Variables
y
Example
Graph 3x + 5y  –2
• Graph 3x + 5y = –2 as a
solid line.
• Pick a point not on the
graph: (0,0), but just
barely
• Test it in the original
inequality.
3(0) + 5(0) > –2, 0 > –2
• False, so shade the side
that does not contain (0,0).
(0, 0)
x
Linear Equations in Two Variables
y
Example
Graph 3x < 15
• Graph 3x = 15 as a
dashed line.
• Pick a point not on the
graph: (0,0)
• Test it in the original
inequality.
3(0) < 15, 0 < 15
• True, so shade the side
containing (0,0).
(0, 0)
x
Graph this:
3x  5y  15