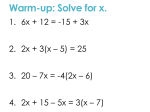Download MTH 100 CBI

MTH 100
Linear Inequalities In One Variable
Objectives
1. Determine if a Given Value is a Solution to a
Linear Inequality.
2. Graph the Solution Set of an Inequality on a
Number Line.
3. Use Interval Notation to Express the Solution
Set of an Inequality.
4. Solve Linear Inequalities in One Variable.
Overview
• Linear inequalities are very similar to linear
equations, with three distinct differences:
1. Instead of “=“, you have “<“, “>”, “<“, or “>”;
2. When you divide (or multiply) both sides by a
negative, you must reverse your inequality sign;
3. After you solve your inequality (still isolating the
variable), you graph your solution (Objective 2)
and write your solution in interval notation
(Objective 3).
Objective 1
• Verifying a given a number is a solution to an
inequality is exactly the same as an equation:
substitute the given value. If the resulting
statement is true, the number is a solution.
Objective 2
• <: open circle (parenthesis), shade to the left
• >: open circle (parenthesis), shade to the right
• <: closed circle (square bracket), shade to the
left
• >: closed circle (square bracket), shade to the
right
Objective 3
• Interval notation is another way to express the
solution set of an inequality.
• Important things to remember:
1. “what’s on the left, what’s on the right”;
2. -∞ is way out to the left, ∞ is way out to the
right (always use parentheses).
Examples (Putting it all together)
4(b  2)  5b  6b  8
4  7w w
  20
5
3
11  7 x
8 
 1
3