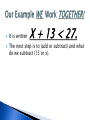Download 6-1 Solving Inequalities by Addition and Subtraction

GOAL: Solve linear inequalities by using
addition and subtraction.
What is the difference in =, <, >, <, >.
= means equals they are the same like 7 = 7.
< means less than like 7 < 9.
> means greater than like 7 > 5.
< means less than or equal to like 7 < 7 or 7 <
9
> means greater than or equal to like 7 > 7 or
7 > 5.
 NOW LETS LOOK AT AN EQUATION!!!!!!!!!!!!
 t – 45 < 13.

The first step is to add
45 to both sides.
We get t = 58.
The first step is to add
45 to both sides.
We get t < 58.
This is a easy one step
equation.
We solved for t.
Don’t let the sign throw
you off it is still a one
step equation that is
being solved for t.
t – 45 = 13
t – 45 < 13


If any number is added to each side of a true
inequality, the resulting inequality is also
true.
For all numbers a, b, and c, the following are
true.
1. If a > b, then a + c > b + c.
2. If a < b, then a + c < b + c.
Example: 2 < 7
2+6<7+6
8 < 13
Solve 7 < x – 4. Then graph it on a number
line.
7<x–4
Original inequality
7 + 4 < x – 4 + 4 add 4 to each side.
11 < x
Solved (done but have to graph).
-25 -20 -15 -10
-5
0
5
10
15
20
25


If any number is subtracted from each side of
a true inequality, the resulting inequality is
also true.
For all numbers a, b, and c, the following are
true.
1. If a > b, then a - c > b - c.
2. If a < b, then a - c < b - c.
Example: 17 > 8
17 - 5 > 8 - 5
12 > 3
Solve 5p + 7 > 6p. Then graph the solution.
5p + 7 > 6p original inequality
5p + 7 – 5p > 6p - 5p subtracted 5p from both
sides.
7> p DONE (BUT HAVE TO GRAPH!!!!!!!)



Our first step is to
Then we can solve.
Write
Equation
this as an
.


It is written
X + 13 < 27.
The next step is to (add or subtract) and what
do we subtract (13 or x).



We do subtract 13.
If we subtract 13 from one side we must
subtract 13 from the other
.
SIDE



X + 13 -13 < 27 - 13
Then we combine the like terms 27 and a
subtracted 13 (because the 13 was added to
the other side). And we GET that 27 – 13 is
14
.



Our answer is x < 14.
Let Check it take any number smaller than 14
and plug it in to the problem. Pick any
number again less than 14. I say 13.
13+13=26 so is 26 < 27.
YES

IT IS!!!!!
We have just work a problem together now
its your turn by yourself.